Abstract
A twin boundary in one of the layers of a twisted van der Waals heterostructure separates regions with near opposite inter-layer twist angles. In a MoS2/WSe2 bilayer, the regions with  and
and 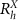 stacking registry that defined the sub-lattices of the moiré honeycomb pattern would be mirror-reflected across such a twist boundary. In that case, we demonstrate that topologically protected chiral moiré exciton states are confined at the twist boundary. These are one-dimensional and uni-directional excitons with opposite velocities for excitons composed by electronic states with opposite valley/spin character, enabling intrinsic, guided, and far reaching valley-polarized exciton currents.
stacking registry that defined the sub-lattices of the moiré honeycomb pattern would be mirror-reflected across such a twist boundary. In that case, we demonstrate that topologically protected chiral moiré exciton states are confined at the twist boundary. These are one-dimensional and uni-directional excitons with opposite velocities for excitons composed by electronic states with opposite valley/spin character, enabling intrinsic, guided, and far reaching valley-polarized exciton currents.
Export citation and abstract BibTeX RIS
1. Introduction
Recent advances in fabrication and manipulation of two-dimensional (2D) materials have enabled precisely controlled stacking and twisting of transition-metal dichalcogenides (TMDs) in van der Waals (vdW) hetero-bilayers [1–3]. In such atomic scale systems, the moiré pattern created by the mismatch between the crystal lattices of the stacked layers plays an important role [4, 5]: it produces an in-plane potential landscape for inter-layer excitons (ILEs), with potential minima at the vertices of a honeycomb superlattice which, in the case of MoS2/WSe2 vdW hetero-bilayers, is formed by regions with either  or
or 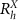 stacking [6]. Since these two stacking registries form different energy minima, the band structure resulting from such a moiré potential exhibits a gapped Dirac cone for the lowest-energy moiré exciton [7, 8]. These moiré excitons were experimentally evidenced e.g. in [9], in the series of exciton peaks associated to ILE confined in the minimum of the moiré potential landscape, as well as in [10] through changes in magnetic field dependence of exciton peaks as a function of the twist angle. Previous works have proposed that moiré-trapped excitons could be used as quantum simulators of many-body physics, and as coherent quantum emitters [7, 11–13]. In general, the synergy between opto-electronics and twistronics encountered in such moiré trapped ILEs has made them an exciting topic of research towards control and enhancement of light-matter interactions in 2D semiconductors [14–16].
stacking [6]. Since these two stacking registries form different energy minima, the band structure resulting from such a moiré potential exhibits a gapped Dirac cone for the lowest-energy moiré exciton [7, 8]. These moiré excitons were experimentally evidenced e.g. in [9], in the series of exciton peaks associated to ILE confined in the minimum of the moiré potential landscape, as well as in [10] through changes in magnetic field dependence of exciton peaks as a function of the twist angle. Previous works have proposed that moiré-trapped excitons could be used as quantum simulators of many-body physics, and as coherent quantum emitters [7, 11–13]. In general, the synergy between opto-electronics and twistronics encountered in such moiré trapped ILEs has made them an exciting topic of research towards control and enhancement of light-matter interactions in 2D semiconductors [14–16].
Often, atomically thin materials exhibit defect lines and grain or twin boundaries [17, 18] that separate adjacent regions with different lattice orientations. Although great effort has been put into the theoretical understanding of mechanical and electronic properties of grain boundaries in monolayer graphene [19, 20] and TMDs [21], the role of extended lattice defects in vdW hetero-bilayers is yet to be investigated in greater detail. In particular, the fact that defect lines due to chalcogen vacancies in monolayer TMDs lead to a misorientation angle in the lattice crystal [21, 22] brings the prospect of spatially engineering the inter-layer twist angles in TMD vdW hetero-bilayers. This can be realized by stacking a TMD monolayer with a defect line or a twin boundary over a pristine monolayer of another TMD using layer transfer techniques [23]. Such a hetero-bilayer would then contain 'twist boundaries' between regions where moiré excitons may behave strikingly differently, due to the locally different inter-layer twist angles.
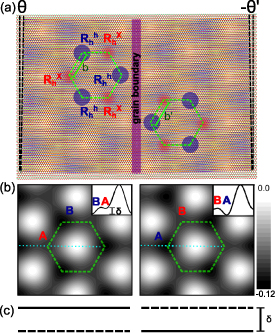
In this Letter, we ask a subsequent question: what physics is then to be expected at the twist-boundary itself? To illuminate this, we theoretically investigate moiré excitons in a MoS2/WSe2 vdW hetero-bilayer where one of the layers contains a twin boundary, as illustrated in figure 1(a). The twin boundary separates the system into two regions with opposite signs of the inter-layer twist angle. As a consequence, moiré exciton states exhibit opposite pseudo-spin character in the two regions. As we will demonstrate, this leads to a 'topologically protected, confined moiré exciton state' lying exactly at the boundary. Such confined moiré excitons have a twist-tunable velocity with spin-dependent direction along the twist boundary, making the latter a rather convenient and versatile platform for 'both' exciton transport and spintronics.
Figure 1. (a) Sketch of the twisted MoS2-WSe2 hetero-bilayer with a twin boundary in the MoS2 layer. As a consequence, twist angle θ on the left side of the boundary changes to twist angle  on the right side, and the
on the right side, and the 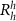 and
and 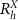 stacking regions at the vertices of the moiré honeycomb lattice (dashed line) are mirror-reflected. (b) Greyscale map of the moiré potential landscape for ILE on two sides of the twist boundary. Regions with
stacking regions at the vertices of the moiré honeycomb lattice (dashed line) are mirror-reflected. (b) Greyscale map of the moiré potential landscape for ILE on two sides of the twist boundary. Regions with  stacking, in the center of each moiré hexagon (dashed line), exhibit maximal potential (white), whereas the potential minima (dark) are in the
stacking, in the center of each moiré hexagon (dashed line), exhibit maximal potential (white), whereas the potential minima (dark) are in the 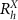 and
and  regions. Insets show the potential profile along the indicated dotted lines. δ denotes the energy difference between the minima at the A and B sites of the moiré hexagon. (c) The energy gaps on two sides of the twist boundary are the same for any θ and
regions. Insets show the potential profile along the indicated dotted lines. δ denotes the energy difference between the minima at the A and B sites of the moiré hexagon. (c) The energy gaps on two sides of the twist boundary are the same for any θ and  , but the pseudo-spin character of the involved bands is different, as represented by solid and dashed lines. In such a case, the confined moiré exciton is expected right at the twist boundary.
, but the pseudo-spin character of the involved bands is different, as represented by solid and dashed lines. In such a case, the confined moiré exciton is expected right at the twist boundary.
Download figure:
Standard image High-resolution imageControllable transport of excitons represents a major development towards signal processing based on optics, rather than on electronics, which is fundamental for faster communication technologies. Uni-directional transport of excitons in vdW hetero-bilayers has been proposed and experimentally observed [24] by using a non-uniform perpendicular electric field to guide the excitons. Our proposal, using moiré exciton that is confined and propagating along the twist boundaries, represents a viable yet advantageous alternative for exciton transport. Besides being energy efficient (not requiring any external drive), our concept provides control over exciton currents composed by spin-polarized electronic states that are topologically protected against back-scattering along the twist boundary.
2. Theoretical backbone
As sketched in figure 1(a), the moiré pattern on each side of the twist boundary is composed of regions with  (blue) and
(blue) and  (red) stacking registry, forming two interspersed triangular sub-lattices which, combined, yield a honeycomb moiré superlattice. Due to the opposite sign of the twist angles, those sub-lattices are mirror-reflected across the twist boundary. The energy minima for ILEs in the moiré potential landscape are found where the crystal exhibits one of these two stacking registries, with
(red) stacking registry, forming two interspersed triangular sub-lattices which, combined, yield a honeycomb moiré superlattice. Due to the opposite sign of the twist angles, those sub-lattices are mirror-reflected across the twist boundary. The energy minima for ILEs in the moiré potential landscape are found where the crystal exhibits one of these two stacking registries, with  being the one with the lowest energy, as shown in the greyscale map in figure 1(b). Details on the calculation of the moiré potential landscape are given in the
being the one with the lowest energy, as shown in the greyscale map in figure 1(b). Details on the calculation of the moiré potential landscape are given in the 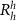 and
and  for this choice of materials is δ = 0.022 eV. In principle, other combinations of TMDs, with twist angles close to either 0∘ or to 60∘ (namely, with a moiré pattern of H-type stacking registries) are also expected to produce results qualitatively similar to those we will discuss here, provided the resulting potential landscape for the exciton, originating from their moiré patterns, also exhibits a honeycomb lattice of significantly deep confining potentials [7]. However, we found the choice of a MoS2/WSe2 vdW heterostructure to be particularly convenient, since we verified, with standard ab initio calculations, that the gap in this combination of materials remains direct at the K-point of the Brillouin zone for all stacking configurations considered here, which helps us to avoid possible complications originating e.g. from indirect exciton states.
for this choice of materials is δ = 0.022 eV. In principle, other combinations of TMDs, with twist angles close to either 0∘ or to 60∘ (namely, with a moiré pattern of H-type stacking registries) are also expected to produce results qualitatively similar to those we will discuss here, provided the resulting potential landscape for the exciton, originating from their moiré patterns, also exhibits a honeycomb lattice of significantly deep confining potentials [7]. However, we found the choice of a MoS2/WSe2 vdW heterostructure to be particularly convenient, since we verified, with standard ab initio calculations, that the gap in this combination of materials remains direct at the K-point of the Brillouin zone for all stacking configurations considered here, which helps us to avoid possible complications originating e.g. from indirect exciton states.
Such a honeycomb superlattice of confining potentials for ILEs in each side yields an energy dispersion for the moiré exciton which exhibits a gap given by the difference δ between the energy minima of the potential landscape, thus resembling that of a Dirac fermion with non-zero mass. Such gapped Dirac cone exhibits a conserved topological charge whose sign depends on the sign of δ. However, due to the changing sign of the twist angle across the twist boundary, the pseudo-spin of this Dirac-like quasi-particle is flipped from one side to the other, and so is the sign of the topological charge. This is illustrated by solid and dashed lines in figure 1(c), representing the pseudo-spin character of the band edges of the gapped moiré exciton band structure across grain the boundary. In fact, this situation is similar to the one where a staggered, gap-opening potential, e.g. due to a BN or SiC substrate, changes sign across a defect line in the substrate, thus changing the sign of the mass term in the Dirac-like Hamiltonian for low-energy electrons [25, 26]. It is also equivalent to the case of bilayer graphene where the inter-layer bias changes sign across a line [27–30]. In both latter cases topologically protected states were found, with energy lower than the gap δ in each side, confined along the interface between the two sides. This is a consequence of the sign change of the topological charge, which produces an in-gap chiral channel along the boundary [31]. In the case of bilayer graphene, these states were experimentally probed [32, 33] and even proposed as a base for valley filtering and beam-splitting devices [34]. More information on the topological charge of massive Dirac cones and the formation of in-gap confined chiral states can be found e.g. in [35, 36]. As we will demonstrate, a moiré exciton is analogously confined at the twist boundary of the vdW hetero-bilayer sketched in figure 1(a), with a non-zero spin-dependent propagation velocity that can be controlled by the twist angle.
Considering each side of our system as a separate honeycomb moiré lattice of confining potentials for ILEs, with lattice constant b (left) and b' (right), the moiré excitons obey the tight-binding Hamiltonian [37],
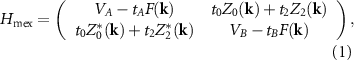
where t0 (t2) are the first (third) nearest-neighbor hoppings, tA
and tB
are the second nearest-neighbor hoppings between sites of the A and B sub-lattices, and the on-site potentials have opposite sign for different sub-lattices,  and
and  (changing signs across the twist boundary). The structure factors for this Hamiltonian are
(changing signs across the twist boundary). The structure factors for this Hamiltonian are
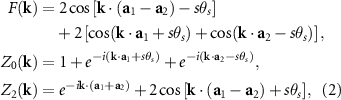
where  and
and  are the moiré lattice vectors and the spin-dependent
are the moiré lattice vectors and the spin-dependent  term originates from the complex part of the hopping parameters of the moiré exciton [7, 38], with spin sign
term originates from the complex part of the hopping parameters of the moiré exciton [7, 38], with spin sign  . Without loss of qualitative generality, we assume
. Without loss of qualitative generality, we assume 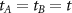 . The band structure obtained by diagonalization of
. The band structure obtained by diagonalization of  in equation (1) exhibits gapped Dirac–Weyl cones at the
in equation (1) exhibits gapped Dirac–Weyl cones at the 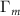 and
and 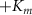 (
( ) points of the moiré Brillouin zone for ILE composed by spin up (down) electronic states, as illustrated by the green (orange) domes in figure 2(a).
) points of the moiré Brillouin zone for ILE composed by spin up (down) electronic states, as illustrated by the green (orange) domes in figure 2(a).
Figure 2. (a) Band structure of the moiré exciton at either side of the considered system, for different spins (arrows). Hexagons represent the moiré Brillouin zone. The band structure exhibits Dirac–Weyl cones with δ gap at  and at the Km
(
and at the Km
( ) vertices for excitons composed by spin up (down) electronics states. (b) Potential profile in two sides of the considered vdW bilayer for different applied electric field.
) vertices for excitons composed by spin up (down) electronics states. (b) Potential profile in two sides of the considered vdW bilayer for different applied electric field.
Download figure:
Standard image High-resolution imageWe point out that the spin label s defined here refers to the spin states of the electrons and holes that compose the exciton, rather than the spin of the exciton itself. The latter is in a spin singlet state and carries zero net spin momentum for the near zero inter-layer twist angles considered here. On the other hand, the electron and hole that form the exciton exhibit a spin polarization directly linked to their valley degree of freedom [39]. As we will discuss further, the K and K' valleys of the first Brillouin zone of the MoS2 and WSe2 crystals can be separately accessed by circularly polarized light in opposite directions, thus allowing one to control the spin character of the electrons and holes in the moiré exciton state.
In the presence of the defect line, the band structures for a given spin state are similar in both sides of the system, differing only by their pseudo-spin nature. Notice that in general  , which causes
, which causes  . Nevertheless, provided the signs of the twist angles in each side of the twist boundary are opposite, the stacking registries of A and B sub-lattices in figure 1 will always be interchanged from one side to the other and, consequently, the pseudo-spin character of the moiré excitons in each side will be opposite. Therefore, consequences of such a twist boundary, and the existence of there confined moiré excitons discussed in this paper, are expected to be ubiquitous for any MoS2/WSe2 vdW hetero-bilayer where one of the layers contains a grain or twin boundary. Moreover, with current layer transfer techniques [23], one can always align the two layers in a symmetric way with respect to the twist boundary, such that
. Nevertheless, provided the signs of the twist angles in each side of the twist boundary are opposite, the stacking registries of A and B sub-lattices in figure 1 will always be interchanged from one side to the other and, consequently, the pseudo-spin character of the moiré excitons in each side will be opposite. Therefore, consequences of such a twist boundary, and the existence of there confined moiré excitons discussed in this paper, are expected to be ubiquitous for any MoS2/WSe2 vdW hetero-bilayer where one of the layers contains a grain or twin boundary. Moreover, with current layer transfer techniques [23], one can always align the two layers in a symmetric way with respect to the twist boundary, such that  . Therefore, from here onward, without loss of generality, we will consider the
. Therefore, from here onward, without loss of generality, we will consider the 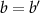 case, as results for the case
case, as results for the case  are qualitatively similar.
are qualitatively similar.
Since the inter-layer distance depends on the stacking registry, the 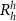 and
and  regions of the moiré pattern will be differently affected by an applied electric field
regions of the moiré pattern will be differently affected by an applied electric field 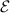 , perpendicular to the vdW hetero-bilayer plane. The potential minima at the A and B sub-lattices illustrated in figure 1(b) depend on the field as
, perpendicular to the vdW hetero-bilayer plane. The potential minima at the A and B sub-lattices illustrated in figure 1(b) depend on the field as 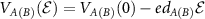 , where
, where 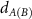 is the inter-layer distance at the A (B) sites. Consequently, the difference between these minima, which determines the gap of the moiré exciton band structure, depends on the field as
is the inter-layer distance at the A (B) sites. Consequently, the difference between these minima, which determines the gap of the moiré exciton band structure, depends on the field as  . Ab initio calculations yield
. Ab initio calculations yield 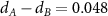 nm for R-type MoS2/WSe2 bilayer, therefore, fields
nm for R-type MoS2/WSe2 bilayer, therefore, fields  V nm−1 are able to invert the gap in both sides and, consequently, flip the pseudo-spin character of the moiré exciton states. This suggests that the moiré exciton bandgap can be conveniently tuned by the external field
V nm−1 are able to invert the gap in both sides and, consequently, flip the pseudo-spin character of the moiré exciton states. This suggests that the moiré exciton bandgap can be conveniently tuned by the external field 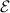 , as demonstrated in figure 2(b), where the potential profile is shown for
, as demonstrated in figure 2(b), where the potential profile is shown for  = 0 (solid), −0.425 V nm−1 (dashed) and −0.85 V nm−1 (dotted line).
= 0 (solid), −0.425 V nm−1 (dashed) and −0.85 V nm−1 (dotted line).
3. Interface-confined moiré excitons
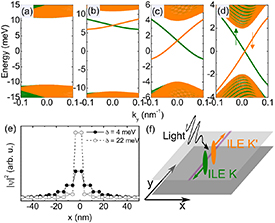
Figure 3(a) shows the band structure of moiré ILE composed by spin up and spin down electronic states in MoSe2/WS2, in the absence of applied electric field and any defect line, in the vicinity of the  point, as obtained by numerical diagonalization of a real-space tight-binding Hamiltonian for the moiré superlattice, assuming periodic boundary conditions, that corresponds to the Bloch Hamiltonian in equation (1). As previously mentioned, the spin up and down electronic states are linked to the K and K' valleys of the monolayer crystals, therefore, the green and yellow bands in figure 3 are equivalently regarded as valley polarized bands. The moiré exciton energies form a δ = 22 meV gapped Dirac–Weyl band structure, as previously discussed. However, in the presence of the twist boundary illustrated in figure 1, the energy spectrum in figure 3(b) for δ = 22 meV exhibits two states inside the gap, one for each spin orientation/valley label of the electronic states that compose the exciton. The energies of these states decrease as the effective gap is reduced by increasing the perpendicular electric field, as shown in figures 3(c) and (d). In the latter, for δ = 4 meV, the gap states appear even at zero momentum and zero energy.
point, as obtained by numerical diagonalization of a real-space tight-binding Hamiltonian for the moiré superlattice, assuming periodic boundary conditions, that corresponds to the Bloch Hamiltonian in equation (1). As previously mentioned, the spin up and down electronic states are linked to the K and K' valleys of the monolayer crystals, therefore, the green and yellow bands in figure 3 are equivalently regarded as valley polarized bands. The moiré exciton energies form a δ = 22 meV gapped Dirac–Weyl band structure, as previously discussed. However, in the presence of the twist boundary illustrated in figure 1, the energy spectrum in figure 3(b) for δ = 22 meV exhibits two states inside the gap, one for each spin orientation/valley label of the electronic states that compose the exciton. The energies of these states decrease as the effective gap is reduced by increasing the perpendicular electric field, as shown in figures 3(c) and (d). In the latter, for δ = 4 meV, the gap states appear even at zero momentum and zero energy.
Figure 3. (a) Moiré exciton band structures for ILE in 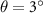 uniformly twisted MoS2/WSe2 hetero-bilayer. (b)–(d) Band structure for the sample with a twin twist boundary, with δ tuned by electric field to 22, 8 and 4 meV, respectively. Results for ILE composed by spin up and down electronic states are shown as green and orange curves, respectively. (e) Probability density distribution of the moiré exciton state confined at the twist boundary, for two values of the gap δ. Symbols are the values in each site of the moiré potential minima along the armchair direction of the honeycomb moiré lattice. (f) Sketch of the propagating inter-layer excitons in K (green) and K' (orange) valleys, which are linked to spin up and down electron–hole states, respectively.
uniformly twisted MoS2/WSe2 hetero-bilayer. (b)–(d) Band structure for the sample with a twin twist boundary, with δ tuned by electric field to 22, 8 and 4 meV, respectively. Results for ILE composed by spin up and down electronic states are shown as green and orange curves, respectively. (e) Probability density distribution of the moiré exciton state confined at the twist boundary, for two values of the gap δ. Symbols are the values in each site of the moiré potential minima along the armchair direction of the honeycomb moiré lattice. (f) Sketch of the propagating inter-layer excitons in K (green) and K' (orange) valleys, which are linked to spin up and down electron–hole states, respectively.
Download figure:
Standard image High-resolution imageIn all cases, the probability density distribution of the gap states is highly confined at the twist boundary, although for a δ = 4 meV gap, it is spread over more minima of the moiré potential, as shown in figure 3(e). In this case, the gap is lower than the first nearest-neighbor hopping energy t0 between moiré potential minima, which allows us to investigate the system using a linear approximation on the Bloch Hamiltonian in equation (1) that yields a Dirac–Weyl Hamiltonian for low momentum moiré excitons, i.e. in close vicinity of the  point of the moiré Brillouin zone (mBZ). Such low momentum excitons are expected due to the low momentum of the photon exciting the exciton. Details on this approximation are given in the
point of the moiré Brillouin zone (mBZ). Such low momentum excitons are expected due to the low momentum of the photon exciting the exciton. Details on this approximation are given in the 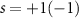 spin state. This explains the numerically obtained energy dispersion of the moiré exciton states inside the gap in figure 3(d), which are monotonically decreasing (increasing) functions of ky
for spin up (down) states, approximately linear around
spin state. This explains the numerically obtained energy dispersion of the moiré exciton states inside the gap in figure 3(d), which are monotonically decreasing (increasing) functions of ky
for spin up (down) states, approximately linear around 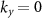 . The linear energy dispersion of the exciton states inside the gap as a function of ky
indicates that these are propagating moiré excitons, with non-zero group velocity, even at
. The linear energy dispersion of the exciton states inside the gap as a function of ky
indicates that these are propagating moiré excitons, with non-zero group velocity, even at  . For each spin orientation of the electronic states that compose the exciton, only one confined moiré exciton band is found inside the gap, and its velocity is opposite for opposite spin states. Thus, even a zero-momentum moiré exciton is trapped at the interface and propagates with non-zero velocity, resulting in a valley-polarized exciton current, where excitons are composed by electronic states with opposite spin-polarization for different valleys, as illustrated in figure 3(f).
. For each spin orientation of the electronic states that compose the exciton, only one confined moiré exciton band is found inside the gap, and its velocity is opposite for opposite spin states. Thus, even a zero-momentum moiré exciton is trapped at the interface and propagates with non-zero velocity, resulting in a valley-polarized exciton current, where excitons are composed by electronic states with opposite spin-polarization for different valleys, as illustrated in figure 3(f).
From the analytical solution for the propagating moiré exciton states, one observes that their velocity does not depend on the bandgap δ for  , i.e. in the case where the zero energy propagating moiré excitons are observed as Dirac–Weyl quasi-particles (see
, i.e. in the case where the zero energy propagating moiré excitons are observed as Dirac–Weyl quasi-particles (see 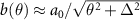 , where
, where  , and a0 (
, and a0 ( ) is the inter-atomic distance in MoS2 (WSe2). For twist angles between zero and 3∘, one obtains t0 values from 2.78 meV to 5.1 meV, respectively [37]. Even so, we have verified that propagation velocities are only weakly dependent on θ, with values between ≈50 nm ps−1 for near-zero twist angles to ≈58 nm ps−1 at the
) is the inter-atomic distance in MoS2 (WSe2). For twist angles between zero and 3∘, one obtains t0 values from 2.78 meV to 5.1 meV, respectively [37]. Even so, we have verified that propagation velocities are only weakly dependent on θ, with values between ≈50 nm ps−1 for near-zero twist angles to ≈58 nm ps−1 at the 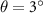 case considered here. For comparison, this velocity is roughly 20 times smaller than the Fermi velocity for Dirac-like low-energy electrons in monolayer graphene. Since the inter-layer exciton lifetime is typically of the order of hundreds of pico-seconds [40–42], one can estimate that such confined inter-layer moiré exciton, if it inherits lifetimes of the same order of magnitude, is thus expected to easily propagate several microns along the interface before recombination, which thus facilitates the experimental verification of this phenomenon, as well as its use in future technologies.
case considered here. For comparison, this velocity is roughly 20 times smaller than the Fermi velocity for Dirac-like low-energy electrons in monolayer graphene. Since the inter-layer exciton lifetime is typically of the order of hundreds of pico-seconds [40–42], one can estimate that such confined inter-layer moiré exciton, if it inherits lifetimes of the same order of magnitude, is thus expected to easily propagate several microns along the interface before recombination, which thus facilitates the experimental verification of this phenomenon, as well as its use in future technologies.
4. Discussion
As previously discussed, if the twist angles on two sides of the twist boundary are not symmetric, one has an interface between two regions with different moiré lattice constants, thus leading to different hopping parameters on each side. However, our numerical results show that the interface-confined states are still present in this case, with propagation velocities that match those of the symmetric problem, with an angle θ given by the average of the twist angles on the two sides.
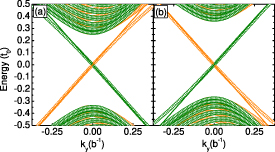
As shown in figure 2(b), an electric field can be used to tune the energy difference between A and B sub-lattices minima and, consequently, the moiré exciton bandgap δ. Figure 4(a) shows our numerical results for propagating moiré excitons in twisted MoS2/WSe2 hetero-bilayer under 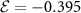 V nm−1, which corresponds to a
V nm−1, which corresponds to a  gapped system, where, since
gapped system, where, since  , the analytical results from the Dirac–Weyl Hamiltonian provide a good approximation of the numerical results. Indeed, analytical results in the Dirac–Weyl approximation are shown as solid lines and agree well with the numerical results (see
, the analytical results from the Dirac–Weyl Hamiltonian provide a good approximation of the numerical results. Indeed, analytical results in the Dirac–Weyl approximation are shown as solid lines and agree well with the numerical results (see
Figure 4. Moiré exciton dispersion for twisted MoS2/WSe2 hetero-bilayer, obtained by tight-binding calculations (symbols) along the twist boundary, for two values of applied electric field 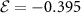 V nm−1 (a) and −0.525 V nm−1 (b). Solid lines show the approximate analytical dispersion of the confined moiré exciton.
V nm−1 (a) and −0.525 V nm−1 (b). Solid lines show the approximate analytical dispersion of the confined moiré exciton.
Download figure:
Standard image High-resolution imageWe point out that the interface-confined states investigated here at the twin boundary between regions with near-zero inter-layer twist angles are fundamentally different from the type-II excitons expected to occur at the interface between TMDs in a side-by-side heterostructure [43, 44]. On the other hand, they bear a resemblance to those found at the lateral interface between R-type and H-type stacked vdW hetero-bilayers, which have been discussed in [45]. While, in the case studied here, the moiré excitons are confined even in the absence of fields and the application of the perpendicular electric field switches the sign of δ in both sides of the interface, thus reversing the propagation direction of the spin up and spin down interface states, such field in the R-type/H-type vdW hetero-bilayers is shown to change the sign of δ only in the R-stacking side [45], which can be used to turn off the interface confined gap states, since these states occur only when δ in the R-stacking and H-stacking sides have opposite signs.
It is important to recall that grain boundaries and lattice defects can produce confined states inside the gap of monolayer semiconductors (as observed e.g. in monolayer WSe2 [46]) or even to modify the bandgap of the material [47]. We note that our analysis concerns an inter-layer exciton that is trapped by the gap in the moiré band structure, rather than by the gap of the hetero-bilayer or its monolayer constituents. Provided that such inter-layer states have a different energy compared to the defect states, the results discussed here will hold. The mechanism of confinement in our case introduces a linear dispersion on the trapped exciton, which yields uni-directional exciton propagation. The fact that there is only one energy band in figure 3(d) for each moiré exciton valley state, with a single velocity direction, suggests that this is a topologically protected state that cannot be scattered back by impurities, such as e.g. chalcogen vacancies at a grain boundary. This absence of backscattering is analogous to the one investigated in details in [48] in the similar context of in-gap states in biased bilayer graphene.
Notice that these valley-polarized propagating excitons, composed by spin-polarized electronic states, at the twist boundary actually simply require an interface between two adjacent honeycomb lattices of exciton confining potentials with (a) sizeable hopping energies and (b) energy differences between A and B sub-lattice potentials that interchange sign across the interface. The vdW hetero-bilayer with a twist boundary naturally has these two ingredients, but one expects analogous results in any artificial lattice with these same characteristics, produced e.g. by periodic strain patterns or other local confining potentials.
By taking advantage of the optical selection rules of TMDs, one can produce initial exciton states that are fully valley polarized and, consequently, composed by spin-polarized electronic states, by exciting the system with circularly polarized light [39, 49, 50]. Opposite valley/spin states are accessible by using circular light polarization in the opposite direction, thus allowing one to control the exciton transport direction via light polarization. Nevertheless, even when both K and K' excitons are accessed as the initial state, e.g. for linear light polarization, our results demonstrate that the exciton current in this system will eventually polarize valley/spin states by producing currents that run in opposite directions for moiré excitons lying in different valleys.
5. Conclusions
Twisted van der Waals hetero-bilayers may contain a novel type of extended defect, namely a twist boundary formed by a grain or twin boundary in one of the layers. We demonstrated that such an extended defect, separating two regions of opposite inter-layer twist angle, confines a topologically protected moiré exciton state. Moreover, this moiré exciton has a non-zero Fermi velocity along the twist boundary, with sign that depends on the spin orientation of the electronic states that compose the exciton. For the materials considered here, and small twist angles, the moiré exciton velocity exceeds 50 nm ps−1, allowing its transport over several microns of distance prior to recombination. This far propagating photo-excited neutral quasi-particle may be one of the key ingredients in the development of novel opto-electronic devices where energy transfer and light transport are of essence, whereas the spin-dependent nature of the propagation opens pathways towards possible spintronic applications.
Acknowledgment
This work was supported by the Research Foundation—Flanders (FWO), and the Brazilian Council for Research (CNPq), through the PQ, universal, and PRONEX/FUNCAP programs.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Appendix
Appendix. Moiré potential landscape
The moiré potential landscape illustrated in figure 1(b) of the main manuscript is given by  , where
, where  is the optical gap of ILEs in the R-stacked hetero-bilayer,
is the optical gap of ILEs in the R-stacked hetero-bilayer, 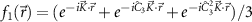 , and
, and 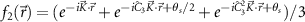 [5]. The
[5]. The 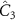 operator represents a 120∘ rotation, and we have defined
operator represents a 120∘ rotation, and we have defined 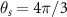 .
.  and
and 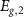 are material dependent and, for R-stacked MoS2/WSe2 hetero-bilayer, are found to be −0.116 eV and −0.094 eV, respectively [7]. The
are material dependent and, for R-stacked MoS2/WSe2 hetero-bilayer, are found to be −0.116 eV and −0.094 eV, respectively [7]. The 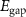 term in
term in  is constant and, therefore, does not play a role in our calculations.
is constant and, therefore, does not play a role in our calculations.
Appendix. Analytical solution within the Dirac–Weyl approximation
When the energy difference between the minima of the honeycomb potential is lower than the first nearest-neighbor hopping energy t0 between them, such as in the δ = 4 meV case in figure 3(d) of the main manuscript, the system can be analytically investigated using a Dirac–Weyl approximate Hamiltonian for low momentum moiré excitons close to the 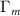 point of the moiré Brillouin zone (mBZ), based on the Bloch Hamiltonian in equation (1). In this case, the structure factors in equation (1) for the left side of our system can be expanded up to first order in
point of the moiré Brillouin zone (mBZ), based on the Bloch Hamiltonian in equation (1). In this case, the structure factors in equation (1) for the left side of our system can be expanded up to first order in 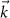 , so the Hamiltonian becomes
, so the Hamiltonian becomes
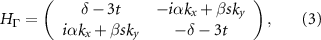
where  ,
,  .
.  is identified as a Dirac–Weyl Hamiltonian, leading to a band structure composed of Dirac–Weyl cones gapped by δ. Similar analysis can be made in the vicinity of the
is identified as a Dirac–Weyl Hamiltonian, leading to a band structure composed of Dirac–Weyl cones gapped by δ. Similar analysis can be made in the vicinity of the  points of the mBZ.
points of the mBZ.
One possible eigenstate of this Hamiltonian, for the left side, is an exponentially increasing pseudo-spinor
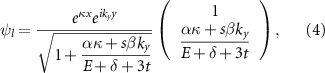
where ![$\kappa = \sqrt{\beta^2k_y^2 - [(E+3t)^2-\delta^2]}/\alpha$](https://content.cld.iop.org/journals/2053-1583/9/2/025012/revision3/tdmac529dieqn76.gif) . For the right side of the system, we choose an exponentially decaying pseudo-spinor ψr
, i.e. with similar form as equation (4), but with
. For the right side of the system, we choose an exponentially decaying pseudo-spinor ψr
, i.e. with similar form as equation (4), but with  and
and 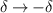 , due to the opposite sign of the twist angle. Assuming the twist boundary at x = 0, one can verify that these exponential solutions at two sides satisfy the continuity boundary condition
, due to the opposite sign of the twist angle. Assuming the twist boundary at x = 0, one can verify that these exponential solutions at two sides satisfy the continuity boundary condition  for four energy states, namely
for four energy states, namely  and
and  , which are found with the requirement that sign
, which are found with the requirement that sign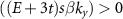 . This requirement forbids the
. This requirement forbids the  solution for
solution for 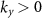 , and
, and  for
for  . Since these flat bands are not continuous along the entire ky
-axis, they are neglected from here onward [25, 29]. Similarly, only the
. Since these flat bands are not continuous along the entire ky
-axis, they are neglected from here onward [25, 29]. Similarly, only the 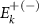 solution is found to be valid for
solution is found to be valid for 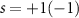 . Moreover, since we are searching for solutions confined at the interface between the two different moiré pattern regions, where the exponential functions in equation (4) decay towards either
. Moreover, since we are searching for solutions confined at the interface between the two different moiré pattern regions, where the exponential functions in equation (4) decay towards either 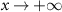 or
or 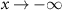 , only solutions with real κ are valid. Nevertheless, this condition is met for
, only solutions with real κ are valid. Nevertheless, this condition is met for 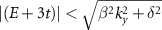 , which also holds for the aforementioned
, which also holds for the aforementioned 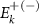 state. Therefore, even though the boundary condition suggests the existence of four different solutions, we end up with only one state inside the gap, namely
state. Therefore, even though the boundary condition suggests the existence of four different solutions, we end up with only one state inside the gap, namely 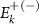 , which is a linearly increasing (decreasing) band for a
, which is a linearly increasing (decreasing) band for a  spin state.
spin state.
Notice that, in order to match the numerical results in figure 4 of the main manuscript, one has to make a hardshift on the numerical energy spectra, as to set the energy reference as the point where the two interface-confined states cross.
From the obtained expression for the 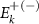 states, one infers that, within the regime where the propagating moiré exciton behaves as a Dirac–Weyl quasi-particle, its velocity does not depend on the bandgap δ.
states, one infers that, within the regime where the propagating moiré exciton behaves as a Dirac–Weyl quasi-particle, its velocity does not depend on the bandgap δ.