Combining asymptotic linearized inversion and full waveform inversion

Métivier, L.; Brossier, R.; Virieux, J.

doi:10.1093/gji/ggv106

Abstract

A method for combining the asymptotic operator designed by Beylkin (Born migration operator) for the solution of linearized inverse problems with full waveform inversion is presented. This operator is used to modify the standard L² norm that measures the distance between synthetic and observed data. The modified misfit function measures the discrepancy of the synthetic and observed data after they have been migrated using the Beylkin operator. The gradient of this new misfit function is equal to the cross-correlation of the single scattering data with migrated/demigrated residuals. The modified misfit function possesses a Hessian operator that tends asymptotically towards the identity operator. The trade-offs between discrete parameters are thus reduced in this inversion scheme. Results on 2-D synthetic case studies demonstrate the fast convergence of this inversion method in a migration regime. From an accurate estimation of the initial velocity, three and five iterations only are required to generate high-resolution P-wave velocity estimation models on the Marmousi 2 and synthetic Valhall case studies.

Numerical solutions, Inverse theory, Numerical approximations and analysis, Computational seismology, Wave scattering and diffraction, Wave propagation

1 INTRODUCTION

Full Waveform Inversion (FWI) has reached today sufficient maturity for being routinely included in the industrial seismic imaging workflow. The method is based on the iterative minimization of the misfit between recorded and synthetic seismograms. The synthetic seismograms are computed through the solution of partial differential equations describing the seismic wave propagation. The minimization of the misfit function is performed over a set of parameters of these equations, which control the wave propagation. This simple formalism allows one to quantitatively estimate physical parameters such as P- and S-wave velocities, density, attenuation and anisotropy coefficients, with a resolution of the order of the wavelength.

Appearing in the early work of Lailly (1983) and Tarantola (1984), FWI was initially thought of as intractable for realistic applications. At that time, the lack of long offsets and low frequencies in the recorded seismic data were responsible for a large gap between the low and high part of the spatial spectrum (wavenumber) which could be reconstructed (Jannane et al.1989). Besides, the computational cost of the method was seen as a major limitation (Gauthier et al.1986).

The simultaneous development of wide-aperture broadband acquisition systems and high-performance computing facilities during the last three decades allowed for the successful application of FWI to real data in the 2-D acoustic and elastic approximations (Operto et al.2004, 2006; Ravaut et al.2004; Gao et al.2006; Brossier et al.2009; Prieux et al.2011; Plessix et al.2012; Prieux et al.2013a,b) as well as in the 3-D acoustic approximation (Sirgue et al.2008; Plessix & Perkins 2010; Vigh et al.2010; Warner et al.2013). An overview of the FWI method and its application to synthetic and real case study data has been proposed by Virieux & Operto (2009).

The two key ingredients involved in the FWI process are first- and second-order derivatives of the misfit function, namely the gradient and the Hessian operators. These ingredients are used at each iteration to construct the update that corrects the current subsurface model estimation. The gradient is built as the cross-correlation of the data residuals with the signals that would be scattered by localized perturbations missing in the initial subsurface model. In this sense, the model update provided by the gradient is an interpretation of the unexplained part of the seismograms (the residuals) in terms of single scattering effects. However, the gradient does not contain any information about the true amplitude of the missing perturbations, and the single scattering assumption is violated as soon as multiscattered arrivals have been recorded. In addition, when multiple classes of parameters are involved in the reconstruction process, trade-offs are expected as the signal scattered by a local perturbation of one parameter class may resemble the signal scattered by a perturbation of another parameter class. A review of these difficulties, especially in the multiparameter inversion framework, is given in Operto et al. (2013) and Alkhalifah & Plessix (2014).

Better accounting for the influence of the Hessian operator in the inversion process should help to mitigate these difficulties. Since the pioneering work of Pratt et al. (1998), numerous studies have been proposed on effects of the inverse Hessian operator. Applying this operator to the gradient restores the amplitude of the perturbations and corrects for artefacts generated by second-order reflections. In addition, it helps refocus the model update and mitigates the trade-offs between parameter classes, as the Hessian operator accounts for spatial and parameter trade-offs.

These well-identified properties have led the FWI community to improve the Hessian operator approximation in the inversion schemes, progressively going from pre-conditioned steepest descent using diagonal approximations of the Gauss–Newton operator (Operto et al.2004) or of the pseudo-Hessian operator (Shin et al.2001), to non-linear conjugate gradient methods (Fichtner et al.2008), l-BFGS approximations (Brossier et al.2009) and truncated Newton methods (Métivier et al.2013, 2014; Castellanos et al.2015). The latter method is based on an approximate solution of the linear system associated with the Newton equations. This approximate solution is computed through few iterations of a linear conjugate gradient solver. This only requires the ability to compute efficiently the action of the Hessian operator on a given vector (matrix-free paradigm). This operation requires two additional solutions of the forward problem using second-order adjoint methods (Métivier et al.2012).

Despite the importance of the inverse Hessian operator in FWI, the aforementioned techniques still rely on a quite crude approximation of this operator. Diagonal Gauss–Newton and pseudo-Hessian approaches only account for the diagonal elements. Few gradients (from 3 to 20 in practice) are used to construct the l-BFGS approximation. The number of internal iterations involved in the solution of the Newton equations should not exceed 10–20 for the truncated Newton method to remain computationally feasible. These numbers have to be compared to the actual size of the Hessian operator in realistic applications: after discretization, the Hessian operator is a square matrix of size N = O(10⁶) in 2-D and N = O(10⁹) in 3-D. The imperfect illumination of the subsurface causes this matrix to be poorly conditioned, making difficult to approximate the solution of the Newton equations in such a small number of iterations.

In this study, an alternative approach is investigated. The underlying idea is to consider a modification of the standard FWI misfit function that yields a misfit function with a Hessian operator tending asymptotically towards the identity. The minimization of this modified misfit function is a better conditioned problem compared to the original one. In particular, in the domain of validity of this modified misfit function, the trade-offs between parameters should be reduced.

The modification of the misfit function consists in projecting the observed and synthetic data on the model space, through a migration operator. The misfit function is thus computed as the L² norm of residuals in the model space, instead of being defined in the data space. The migration operator that is used is the one proposed by Beylkin & Burridge (1990), developed in the framework of inversion as an approximate inverse of the Born modelling operator (Beylkin 1985, 1987; Bleistein et al.1985; Bleistein 1987; Beylkin & Burridge 1990; ten Kroode 2012).

The dominant part of the Hessian operator of the modified misfit function (the Gauss–Newton part) is a normal operator associated with a modified Born modelling operator. As a result of the introduction of the migration operator in the misfit function, this modified Born modelling operator matrix is equal to the Born modelling operator left-multiplied by the Beylkin operator. This operator tends asymptotically towards the identity. As a consequence, the normal operator associated with this modified Born operator tends asymptotically towards the identity.

A first attempt to use the Beylkin operator in the framework of least-squares inversion has been proposed by Jin (1992), merging two apparent disconnected methods. The underlying idea was to introduce the asymptotic inverse in the misfit function as a data weighting operator to produce a modified misfit function with a nearly diagonal Hessian operator. Unfortunately, as the weighting operator is a mapping from the data space to the model space, the resulting misfit function depends on the space location, which prevents the use of standard non-linear optimization techniques. A similar idea has also been exploited by Sevink & Herman (1996) for accelerating the solution of a least-squares migration problem.

The strategy proposed here may be interpreted as applying a migration algorithm to the data residuals, meaning that the modelled and the recorded data are compared in the migrated (spatial) domain. This shares some similarities with the Differential Semblance Optimization (DSO) methods introduced by Symes & Carazzone (1991) as a particular Migration Velocity Analysis (MVA) method (Symes 2008). In these methods, however, the philosophy is different. The data are migrated using a particular background velocity model in an extended model space. The quality of the background velocity model is assessed using a semblance criterion defined in this extended image domain (invariance along the offset for instance). This semblance criterion is used to define a new misfit function in the extended image domain, and the background velocity model is updated to reduce this misfit.

In the method presented in this study, the velocity model used to perform the migration is kept constant, equal to the initial guess, throughout the iteration process. The migration of the data residuals could be interpreted as a change of metric for comparing synthetic and observed data. The residuals are projected in the model space along the geodesics defined by selected ray paths. The minimization is performed to fit the converted data in this new space, and the migration is not used to assess the quality of the background model. The quality of this model may be poor: in this case the asymptotic approximation of the Hessian operator will be far from the identity operator. However, throughout the iterative process, FWI may still allow to correct the subsurface model that is inverted.

In Section 2, the main ideas from the work of Beylkin (1985), leading to the definition of an approximate inverse of the Born operator, are exposed. The Section 3 presents how the asymptotic migration operator is used within this context to modify the FWI misfit function yielding a better conditioned minimization problem. Numerical experiments on synthetic case studies are presented in Section 4 in a 2-D acoustic frequency-domain context for the reconstruction of the pressure wave velocity only (mono-parameter inversion). The advantages and the limits of the approach are presented. The introduction of the Beylkin operator within the misfit function acts as a scattering-angle-based filtering on the seismic data. A stronger weight is given to reflection data, detrimental to data associated with diving waves. This hampers the reconstruction of the long wavelength of the models. On the other hand, starting from an accurate initial velocity model, the gain in convergence speed is substantial. This study thus suggests that the method presented here may be well suited in a quantitative migration context, for the reconstruction of high-resolution estimates of the subsurface parameters, as it is the case for instance in Métivier (2011) and Métivier et al. (2011). In addition, it shows that far from the high-frequency regime, the asymptotic approximation has still a significant effect on the conditioning of the FWI problem.

2 LINEARIZED SEISMIC INVERSE PROBLEM

2.1 Definitions and notations

The domain of investigation is defined as

\begin{equation} \Omega \subset \mathbb {R}^n, \end{equation}

(1)

where the dimension is denoted by |$n\in \mathbb {N}$| (in practice n = 2 or n = 3). In the acoustic approximation, the frequency-domain pressure wavefield p(x, ω) is the solution of

\begin{equation} -\frac{\omega ^2 }{\kappa }p-\rm {div} \left(\frac{1}{\rho } \;\nabla \; p \right) = s(x,\omega ), \end{equation}

(2)

where the angular frequency is denoted by ω, the space variable by |$x\in \mathbb {R}^n$|⁠, the density by ρ(x), the source by s(x, ω) and the bulk modulus by κ(x). In the following, the source will be considered as a Dirac impulse such that

\begin{equation} s(x,\omega )=\delta (x-x_{\rm s}). \end{equation}

(3)

Therefore, the source is parameterized only by its position x_s. The receivers are assumed to be located on a part of the border of the domain denoted by ∂Ω_r. Similarly, the sources are assumed to be located on ∂Ω_s. The generic subsurface parameter notation m(x) is used, such that

\begin{equation} m(x)=\left[\frac{1}{\kappa }\;\; \frac{1}{\rho }\right]^{T}. \end{equation}

(4)

The data are defined as a function of the angular frequency ω, the receivers and source positions x_r and x_s respectively, taking its values in the complex plane |$\mathbb {C}$|⁠. This functional space is defined as |$\scr {D}$|⁠. The synthetic data operator is a mapping from the model space |$\scr {M}$| to the data space |$\scr {D}$| such that

\begin{equation} \begin{array}{cccc}\displaystyle d_{{\rm cal}}: & m & \displaystyle \longrightarrow & d_{{\rm cal}}(m) \\ \displaystyle & \scr {M} & \displaystyle \longrightarrow & \scr {D}. \end{array} \end{equation}

(5)

The operator d_cal is referred to as the forward problem operator in the sequel. This operator depends non-linearly on m, as

\begin{equation} d_{{\rm cal}}(m)(x_{\rm r},x_{\rm s},\omega )=p(x_{\rm r},\omega ; x_{\rm s}, m), \end{equation}

(6)

where the solution of eq. (2) for a source located in x_s and a subsurface model m(x) is denoted by p(x_r, ω; x_s, m).

2.2 Linearized inversion

The first step of linearized inversion consists in a linearization of the forward problem operator. The subsurface model m(x) is decomposed as the sum of a background model m₀(x) and a perturbation of this background δm(x) such that

\begin{equation} m(x)=m_{0}(x)+\delta m(x), \end{equation}

(7)

where δm(x) is such that

\begin{equation} \delta m(x)=\left[ \delta \left(\frac{1}{\kappa (x)}\right) \;\; \delta \left(\frac{1}{\rho (x)}\right)\right]^{T}. \end{equation}

(8)

The first-order Taylor development of the forward problem operator is written as

\begin{equation} d_{{\rm cal}}(m)=d_{{\rm cal}}(m_0)+\frac{\partial d_{{\rm cal}}}{\partial m}(m_0) \delta m+ o\left( \Vert \delta m \Vert ^2_{\scr {M}}\right), \end{equation}

(9)

where |$\Vert .\Vert _{\scr {M}}$| denotes the L² norm in the model space |$\scr {M}$|⁠. The operator ∂d_cal/∂m(m) is known as the Born modelling operator or Jacobian operator. It is denoted by J(m) throughout this study. Considering that a data set d_obs has been recorded, and a background model m₀ is known, the linearized inverse problem can be written as the reconstruction of δm such that

\begin{equation} J(m_0)\delta m= d_{{\rm obs}}-d_{{\rm cal}}(m_0). \end{equation}

(10)

The strategy proposed by Beylkin for solving this problem includes three steps.

Use the first-order Born approximation to derive an analytic expression for J(m₀) depending on the Green functions G⁰(x, ω, x_s) and G⁰(x, ω, x_r) associated with eq. (2).
Compute an asymptotic approximation of J(m₀), denoted by |$\scr {J}(m_0)$|⁠, through the asymptotic approximation of the Green functions G⁰(x, ω, x_s) and G⁰(x, ω, x_r).
Compute an approximate left inverse of |$\scr {J}(m_0)$|⁠, denoted by |$\scr {B}(m_0)$|⁠. The latter operator is roughly equivalent to a preserved-amplitude migration operator.

The approximate solution m* of the linearized inverse problem computed by Beylkin is thus

\begin{equation} m^{*}=m_0+\scr {B}(m_0)\left(d_{{\rm obs}}-d_{{\rm cal}}(m_0)\right). \end{equation}

(11)

These three steps are reviewed in the following subsections.

2.3 First-order Born approximation

The first-order Born approximation is commonly used in seismic inverse problems for the linearization of the forward problem [see for instance Symes (1995)]. In this context, the pressure wavefield p(x, ω; x_s, m) is decomposed into a reference pressure wavefield p₀(x, ω; x_s, m) solution of eq. (2) in the reference model m₀ and a perturbation δp(x, ω; x_s, m), such that

\begin{equation} p(x,\omega ; x_{\rm s},m)=p_0(x,\omega ; x_{\rm s},m)+\delta p(x,\omega ; x_{\rm s},m). \end{equation}

(12)

The perturbed wavefield δp(x, ω; x_s, m) is solution of eq. (2) with a new source term depending on model perturbation δm and the reference wavefield p₀(x, ω; x_s, m):

\begin{eqnarray} -\frac{\omega ^2}{\kappa }\delta p- \rm {div} \left(\frac{1}{\rho }\delta p\right)= \omega ^2 \delta \left(\frac{1}{\kappa }\right)p_0+\rm {div} \left(\delta \left(\frac{1}{\rho }p_0\right)\right). \end{eqnarray}

(13)

From eq. (13), we deduce that

\begin{eqnarray} \delta p(x,\omega ; x_{\rm s},m)&=& \int _{\Omega } \omega ^2 \delta \left(\frac{1}{\kappa (y)}\right)G^{0}(x,\omega ,y) G^{0}(y,\omega ,x_{\rm s})\nonumber\\ && -\;\delta \left(\frac{1}{\rho (y)}\right)\nabla G^{0}(x,\omega ,y) \nabla \; G^{0}(y,\omega ,x_{\rm s}) {\rm d}y.\nonumber\\ \end{eqnarray}

(14)

Eq. (14) is an integral representation of the Born modelling operator J(m₀), acting as a mapping from the model space |$\scr {M}$| to the data space |$\scr {D}$|⁠, such that

\begin{eqnarray} \displaystyle J(m_0): \delta m & \longrightarrow & J(m_0)\delta m= \nonumber\\ && \displaystyle \int _{\Omega } \omega ^2 \delta \left(\frac{1}{\kappa (y)}\right)G^{0}(x_{\rm r},\omega ,y) G^{0}(y,\omega ,x_{\rm s})\nonumber\\ && -\;\delta\left(\frac{1}{\rho (y)}\right)\nabla G^{0}(x_{\rm r},\omega ,y) \nabla \; G^{0}(y,\omega ,x_{\rm s}) {\rm d}y. \nonumber\\ \scr {M} &\longrightarrow &\scr {D}. \end{eqnarray}

(15)

2.4 Asymptotic approximation: computation of |$\scr {J}(m_0)$|

The high-frequency approximation is introduced by considering the simple asymptotic approximation of the Green function G⁰(x, ω, y):

\begin{equation} G^{0}(x,\omega ,y)=A(x;y)e^{i\omega T(x;y)}, \end{equation}

(16)

where only one phase is considered. In complex media, more than one phase may be considered. In this introductory study, only the first arrival (from the source point y to the scattering point x in the above expression) is taken into account, although multi-arrival extensions are possible. In the expression (16), the phase term T(x; y) is the solution of the eikonal equation. It can be computed using a fast marching method (Vidale 1988; Podvin & Lecomte 1991) or a fast sweeping method (Zhao 2005) as only the first arrival is considered in this work. As no intrinsic attenuation is accounted for, the amplitude term A(x; y) is related to the geometrical spreading. The geometrical spreading at a point x for a source located in x_s can be evaluated using the true ray connecting x and x_s and the paraxial quantities around this ray. Details on how to compute in practice these quantities are given in Appendix A.

From the expression (16), the gradient of the Green function ∇G⁰(x, ω; y) satisfies

\begin{equation} \nabla G^{0}(x,\omega , y)=\left[\nabla A(x;y)+ i \omega A(x;y)\nabla T(x;y)\right] e^{i\omega T(x;y)}. \end{equation}

(17)

Following the high-frequency approximation, the first term is neglected and the gradient of the Green function is approximated as

\begin{equation} \nabla G^{0}(x,\omega , y)\simeq i \omega A(x;y) \nabla T(x;y) e^{i\omega T(x;y)}. \end{equation}

(18)

Plugging expressions (16) and (18) into eq. (14) yields the relation

\begin{eqnarray} \scr {J}(m_0)\delta m &=& \displaystyle \omega ^2 \int _{\Omega } \frac{1}{\kappa _{0}(y)} A(x_{\rm r},y,x_{\rm s})e^{i\omega T(x_{\rm r},y,x_{\rm s})}\nonumber\\ &&\times \;W^{T}(x_{\rm r},y,x_{\rm s})M_0(y)\delta m(y)\,{\rm d}y, \end{eqnarray}

(19)

where the following compact notations for ray quantities are used:

\begin{eqnarray} A(x_{\rm r},y,x_{\rm s})&=& A(x_{\rm r};y)A(y;x_{\rm s}),\nonumber\\ T(x_{\rm r},y,x_{\rm s})&=& T(x_{\rm r};y)+T(y;x_{\rm s}). \end{eqnarray}

(20)

The scattering matrix W(x_r, y, x_s) is defined as

\begin{equation} W(x_{\rm r},y,x_{\rm s})=\left[1 \quad \cos \theta (x_{\rm r},y,x_{\rm s})\right]^{T}, \end{equation}

(21)

and the diagonal matrix M₀(y) is

\begin{equation} M_0(y)= {\left(\begin{array}{cc}\kappa _0(y) &\quad 0 \\ 0 &\quad \rho _0(y) \end{array}\right)}. \end{equation}

(22)

In the expression of the scattering matrix, the angle θ(x_r, y, x_s) is the illumination angle at the scattering point y, formed by the pair of rays connecting the scattering point y to receiver position x_r and source position x_s as illustrated in Fig. 1. This angle is related to phases T(x_r; y) and T(y; x_s) through the equation

\begin{eqnarray} \nabla T(x_{\rm r};y).\nabla T(y;x_{\rm s})&=&\frac{1}{v_{P}^2(y)} \cos \theta (x_{\rm r},y,x_{\rm s})\nonumber\\ &=&\frac{\kappa _0(y)}{\rho _0(y)}\cos \theta (x_{\rm r},y,x_{\rm s}). \end{eqnarray}

(23)

Figure 1.

Open in new tab Download slide

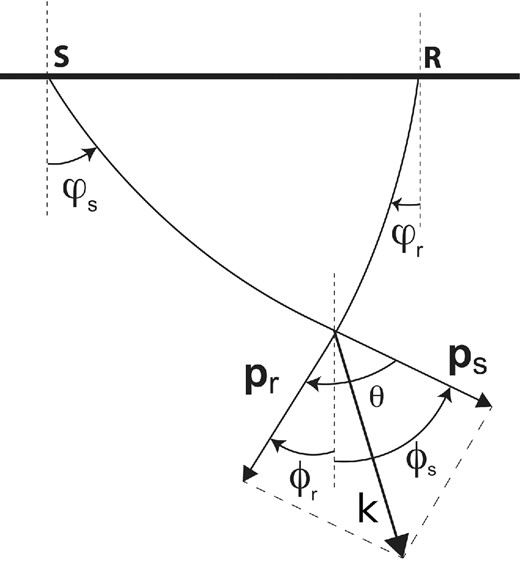
Angles ϕ_r(x_r, x), ϕ_s(x_s, x) and θ(x_r, x, x_s) for a given source–receiver pair.

2.5 Computation of |$\scr {B}(m_0)$|

The asymptotic approximation of the linearized forward operator |$\scr {J}(m_0)$| is

\begin{eqnarray} \scr {J}(m_0): \delta m &\longrightarrow & \scr {J}(m_0)\delta m \nonumber\\ \scr {M} &\longrightarrow & \scr {D}. \end{eqnarray}

(24)

In this section, the computation of an approximate left inverse |$\scr {B}(m_0)$| to |$\scr {J}(m_0)$| is presented. The operator |$\scr {B}(m_0)$| is a mapping from the data space to the model space

\begin{eqnarray} \scr {B}(m_0) d &\longrightarrow & \scr {B}(m_0) d \nonumber\\ \scr {D} &\longrightarrow & \scr {M}. \end{eqnarray}

(25)

Beylkin (1985) defines the operator |$\scr {B}(m_0)$| as a weighted adjoint of |$\scr {J}(m_0):$|

\begin{eqnarray} \left(\scr {B}(m_0) d\right)(x)&=& \int _{\partial \Omega _{\rm r}}\int _{\partial \Omega _{\rm s}}\int _{0}^{\infty } \frac{1}{\omega ^2} \frac{\kappa _{0}(x)h(x_{\rm r},x,x_{\rm s})}{A(x_{\rm r},x,x_{\rm s})}\nonumber\\ &&\times \;e^{-i\omega T(x_{\rm r},x,x_{\rm s})}{\rm d}(x_{\rm r},x_{\rm s},\omega ) W(x_{\rm r},x,x_{\rm s}){\rm d}x_{\rm r} \;{\rm d}x_{\rm s} \;{\rm d}\omega ,\nonumber\\ \end{eqnarray}

(26)

where the weighting function h(x_r, x, x_s) is yet to be described. As in Beylkin (1985), the integral operator |$\scr {F}$| given by the composition of |$\scr {B}(m_0)$| and |$\scr {J}(m_0)$| is introduced:

\begin{eqnarray} \scr {F}: \delta m &\longrightarrow & \scr {B}(m_0)\scr {J}(m_0)\delta m \nonumber\\ \scr {M} &\longrightarrow & \scr {M}. \end{eqnarray}

(27)

Note that the operator |$\scr {F}$| maps |$\scr {M}$| to itself. In what follows, the weighting function h(x_r, x, x_s) is determined so that the operator |$\scr {F}$| is pseudo-differential and tends towards the identity operator. This ensures that the operator |$\scr {B}(m_0)$| is an approximate left inverse of |$\scr {J}(m_0)$|⁠, that is to say a preserved-amplitude migration operator based on the Born modelling operator.

The expression of |$\scr {F}$| at the scattering point x is given by an integral over scattering positions y, expressed as

\begin{eqnarray} (\scr {F}\delta m)(x)&=&\int _{\Omega }\int _{\partial \Omega _{\rm r}}\int _{\partial \Omega _{\rm s}}\int _{0}^{\infty } \frac{\kappa _{0}(x)A(x_{\rm r},y,x_{\rm s})}{\kappa _{0}(y)A(x_{\rm r},x,x_{\rm s})}\nonumber\\ &&\times \; e^{i\omega \left(T(x_{\rm r},y,x_{\rm s})-T(x_{\rm r},x,x_{\rm s})\right)} h(x_{\rm r},x,x_{\rm s}) \nonumber\\ && W(x_{\rm r},x,x_{\rm s})W^{T}(x_{\rm r},y,x_{\rm s})M_0(y)\delta m(y){\rm d}y\;{\rm d}x_{\rm r} \;{\rm d}x_{\rm s} \;{\rm d}\omega .\nonumber\\ \end{eqnarray}

(28)

The most singular part of the operator should be dominant in the asymptotic approximation. The expression of |$\scr {F}$| is thus localized around the scattering point x. This localization amounts to neglect the smoothest terms of the operator (Beylkin 1987). To this purpose, the first-order development of the function T(x_r, x, x_s) is considered,

\begin{equation} T(x_{\rm r},y,x_{\rm s})-T(x_{\rm r},x,x_{\rm s})\simeq \nabla T(x_{\rm r},x,x_{\rm s}).(y-x), \end{equation}

(29)

as well as the zero-order development of the functions depending on y at point x in the integral (28). This yields the following simplified operator:

\begin{eqnarray} (\scr {F}\delta m)(x)&\simeq & M_0(x) \int _{\Omega }\int _{\partial \Omega _{\rm r}}\int _{\partial \Omega _{\rm s}}\int _{0}^{\infty } e^{i\omega \left(\nabla T(x_{\rm r},x,x_{\rm s}).(y-x)\right)}h(x_{\rm r},x,x_{\rm s}) \nonumber\\ &&W(x_{\rm r},x,x_{\rm s})W^{T}(x_{\rm r},x,x_{\rm s}) \delta m(y) {\rm d}y\;{\rm d}x_{\rm r} \;{\rm d}x_{\rm s} \;{\rm d}\omega . \end{eqnarray}

(30)

We recognize the expression of a wavenumber in the argument of the exponential:

\begin{equation} k(\omega ,x_{\rm r},x_{\rm s})=-\omega \nabla T(x_{\rm r},x,x_{\rm s}). \end{equation}

(31)

Following the strategy proposed in Forgues (1996), the following change of variables is considered:

\begin{equation} f: \left(|k|,\Psi ,\theta \right) \longrightarrow f\left(|k|,\Psi ,\theta \right)=\left(\omega ,x_{\rm r},x_{\rm s}\right), \end{equation}

(32)

where

\begin{eqnarray} \theta (x_{\rm r},x,x_{\rm s})&=&\phi _{\rm r}(x_{\rm r},x)-\phi _{\rm s}(x_{\rm s},x),\nonumber\\ \Psi (x_{\rm r},x,x_{\rm s})&=&\frac{\phi _{\rm r}(x_{\rm r},x)+\phi _{\rm s}(x_{\rm s},x)}{2}. \end{eqnarray}

(33)

In this expression, the angles formed with the vertical axis by the ray connecting the receiver (respectively the source) to the point x are denoted by ϕ_r(x_r, x) (respectively ϕ_s(x_s, x)), as presented in Fig. 1. The inverse of this change of variables is denoted by

\begin{equation} f^{-1}: \left(\omega ,x_{\rm r},x_{\rm s}\right) \longrightarrow f^{-1}\left(\omega ,x_{\rm r},x_{\rm s}\right)=\left(|k|,\Psi ,\theta \right). \end{equation}

(34)

Applying this change of variables to eq. (30) yields

\begin{eqnarray} (\scr {F}\delta m)(x) &\simeq & M_0(x) \int _{\Omega }\int _{0}^{\infty }\int _{\Psi _{min}}^{\Psi _{max}}\int _{\theta _{min}}^{\theta _{max}} e^{ik.(x-y)}\nonumber\\ &&\times \;h\left(f(|k|,\Psi ,\theta )\right)\left|\det (Df)(|k|,\Psi ,\theta )\right| \nonumber\\ &&W(f(|k|,\Psi ,\theta ))W^{T}(f(|k|,\Psi ,\theta ))\nonumber\\ &&\times \, \delta m(y) {\rm d}y \;{\rm d}|k| \; {\rm d}\Psi \; {\rm d}\theta , \end{eqnarray}

(35)

where the determinant |$\det (Df)(|k|,\Psi ,\theta )$| is defined by

\begin{equation} \det (Df)(|k|,\Psi ,\theta )= \left| {\begin{array}{ccc}\frac{\partial \omega }{\partial |k|}&\quad \frac{\partial \omega }{\partial \Psi }&\quad \frac{\partial \omega }{\partial \theta } \\ \frac{\partial x_{\rm r}}{\partial |k|}&\quad \frac{\partial x_{\rm r}}{\partial \Psi }&\quad \frac{\partial x_{\rm r}}{\partial \theta } \\ \frac{\partial x_{\rm s}}{\partial |k|}&\quad \frac{\partial x_{\rm s}}{\partial \Psi }&\quad \frac{\partial x_{\rm s}}{\partial \theta } \end{array}} \right|. \end{equation}

(36)

Furthermore, the scattering matrix W(x_r, x, x_s) only depends on the illumination angle θ in the new parameterization (Forgues 1996), a justification of this parameterization selection:

\begin{equation} W(x_{\rm r},x,x_{\rm s})=W\left(\theta (x_{\rm r},x,x_{\rm s})\right). \end{equation}

(37)

The following choice for the function h(x_r, x, x_s) is introduced:

\begin{equation} h(x_{\rm r},x,x_{\rm s})=\frac{|k(x_{\rm r},x,x_{\rm s})|^{n-1}}{{|}\det (Df)(|k|,\Psi ,\theta )|} Z^{-1}\left(\theta _{{\rm max}},\theta _{{\rm min}}\right) M_0^{-1}(x) \end{equation}

(38)

(let us recall that |$n\in \mathbb {N}$| denotes the dimension of the model space and is equal to 2 or 3 in practice). The matrix

\begin{equation} Z\left(\theta _{{\rm max}},\theta _{{\rm min}}\right)= \int _{\theta _{{\rm min}}}^{\theta _{{\rm max}}}W(\theta )W^{T}(\theta )\,d\theta . \end{equation}

(39)

is assumed to be invertible. This yields

\begin{eqnarray} (\scr {F}\delta m)(x)&\simeq & Z^{-1}\left(\theta _{{\rm max}},\theta _{{\rm min}}\right) M_0^{-1}(x)M_0(x)\int _{\theta _{{\rm min}}}^{\theta _{{\rm max}}}W(\theta )W^{T}(\theta )\,{\rm d}\theta \nonumber\\ &&\times \;\int _{\Omega }\int _{0}^{\infty }\int _{\Psi _{{\rm min}}}^{\Psi _{{\rm max}}} |k|^{n-1}e^{ik.(x-y)} \delta m(y){\rm d}y \;{\rm d}|k| \; {\rm d}\Psi .\nonumber\\ \end{eqnarray}

(40)

Straightforward simplifications yield

\begin{eqnarray} (\scr {F}\delta m)(x)&\simeq & \displaystyle \int _{0}^{\infty }\int _{\Psi _{{\rm min}}}^{\Psi _{{\rm max}}} |k|^{n-1}e^{ik.x} \int _{\Omega }e^{-ik.y}\delta m(y){\rm d}y \;{\rm d}|k| \; {\rm d}\Psi \; \nonumber\\ &\simeq & \int _{0}^{\infty }\int _{\Psi _{{\rm min}}}^{\Psi _{{\rm max}}} |k|^{n-1}e^{ik.x} \widehat{\delta m}(k) \;{\rm d}|k| \; {\rm d}\Psi , \end{eqnarray}

(41)

where the symbol |$\; \widehat{.} \;$| denotes the Fourier transform operator. Beylkin (1985) demonstrates that the operator |$\scr {P}$| such that

\begin{equation} \left(\scr {P}\delta m\right)(x)=\int _{0}^{\infty }\int _{\Psi _{{\rm min}}}^{\Psi _{{\rm max}}} |k|^{n-1}e^{ik.x} \widehat{\delta m}(k) \;{\rm d}|k| \; {\rm d}\Psi \end{equation}

(42)

is a pseudo-differential operator which can be represented as the following sum:

\begin{equation} \scr {P}=I+\sum _{i}T_i, \end{equation}

(43)

where the operator I is the identity, and the operators T_i belong to increasingly smooth classes of pseudo-differential operators. This expansion depends on the angles Ψ_min and Ψ_max that characterize the illumination of the subsurface through the acquisition system. In the limit case

\begin{equation} \Psi _{{\rm min}}=0, \;\; \Psi _{{\rm max}}=2\pi , \end{equation}

(44)

we recognize in the double integral of the right-hand side of the expression (42) the Fourier transform in polar coordinates of the Dirac delta function (Forgues 1996). In this case |$\scr {P}=I$|⁠. The result from Beylkin may be interpreted as follows: the pseudo-differential operator |$\scr {P}$| tends asymptotically to the identity as the illumination of the subsurface increases to a complete coverage. From this, it can be deduced that

\begin{equation} \scr {F}\simeq I+\sum _{i}T_i. \end{equation}

(45)

Physically, the incomplete illumination of the subsurface yields a pseudo-differential operator associated with a filtered Dirac function instead of an exact Dirac function. The properties of this filtered Dirac function are studied in Lambaré et al. (2003).

The build-up of the operator |$\scr {B}$| is thus an approximate left inverse to the linear operator |$\scr {J}$|⁠. The explicit computation of the operator |$\scr {B}$| is presented in Appendix B in the 2-D mono-parameter case.

3 MODIFICATION OF THE STANDARD FWI MISFIT FUNCTION

3.1 The FWI problem

The FWI problem is defined as the non-linear least-squares minimization problem

\begin{eqnarray} \min _{m} f(m)&=&\frac{1}{2} \int _{0}^{\infty } \int _{\partial \Omega _{\rm s}} \int _{\partial \Omega _{\rm r}} | d_{{\rm cal}}(x_{\rm r},x_{\rm s},\omega )\nonumber\\ &&-\;d_{{\rm obs}}(x_{\rm r},x_{\rm s},\omega )|^2 {\rm d}x_{\rm r} {\rm d}x_{\rm s} {\rm d}\omega , \end{eqnarray}

(46)

where the complex modulus operation is denoted by the symbol |.|. This problem is solved through local non-linear optimization algorithms. In the framework of these methods, a sequence m_k(x) is built from an initial guess m₀(x), such that

\begin{equation} m_{k+1}=m_k + \alpha _k \Delta m_k, \end{equation}

(47)

where the scalar parameter |$\alpha _k \in \mathbb {R}$| is computed through a line-search or a trust-region globalization process (Bonnans et al.2006; Nocedal & Wright 2006). In the particular case of the Newton method, the parameter α_k is set to 1 and the model update Δm_k is given by

\begin{equation} \Delta m_k=-H(m_k)^{-1} \nabla f(m_k). \end{equation}

(48)

In this expression, the operators H(m_k) and ∇f(m_k) are respectively the Hessian and the gradient of the functional f(m). These two key components of the FWI method can be expressed in terms of the Born modelling operator J(m) as

\begin{eqnarray} \nabla f(m)&=& J^{*}(m)(d_{{\rm cal}}(m)-d_{{\rm obs}}), \nonumber\\ H(m)&=& J^{*}(m)J(m)+\frac{\partial J}{\partial m}(d_{{\rm cal}}(m)-d_{{\rm obs}}). \end{eqnarray}

(49)

3.2 Link with the linearized inverse problem

The usual approximation of the Newton method consists of considering only the first term of the right-hand side in the expression of the Hessian operator. This is referred to as the Gauss–Newton approximation. In this context, the model update at iteration k is the solution of the linear system

\begin{equation} H_{{\rm GN}}(m_k)\Delta m_k=-\nabla f(m_k), \;\; \rm {with} \;\; H_{{\rm GN}}(m)=J^{*}(m)J(m). \end{equation}

(50)

This equation can be rewritten in terms of the Born modelling operator and the model update only:

\begin{equation} J^{*}(m_k)J(m_k)\Delta m_k=-J^{*}(m_k)(d_{{\rm cal}}(m_k)-d_{{\rm obs}}). \end{equation}

(51)

Eq. (51) is important, as it reveals that, in the Gauss–Newton approximation, the model update at iteration k is computed as the least-squares solution of the system:

\begin{equation} J(m_k)\Delta m_k=d_{{\rm obs}}-d_{{\rm cal}}(m_k). \end{equation}

(52)

The first iteration of the Gauss–Newton method thus amounts to compute the subsurface model as

\begin{equation} m_1=m_0+\Delta m_0, \end{equation}

(53)

where Δm₀ satisfies

\begin{equation} J(m_0)\Delta m_0=d_{{\rm obs}}-d_{{\rm cal}}(m_0) \end{equation}

(54)

in the least-squares sense.

The connection with the linearized inversion can be made here. Eq. (54) is similar to the linearized inverse problem (10), where Δm₀ is replaced by δm. These two model updates are two approximate solutions of the same problem. They differ in the approximation used to compute them. In the linearized inverse method proposed by Beylkin, the preserved-amplitude migration operator |$\scr {B}(m_0)$| is used. In the context of the Gauss–Newton method, the solution of this equation in the least-squares sense is computed numerically .

3.3 Introducing the asymptotic inverse within the FWI process

This statement raises the question whether the preserved amplitude migration operator |$\scr {B}(m_0)$| could be used in the FWI process to accelerate its convergence. A first attempt to treat this question was proposed by Jin (1992) and later on pursued by Forgues (1996), Thierry et al. (1999a,b) and Lambaré et al. (2003). In these studies, the inverse problem is defined as the least-squares minimization of the misfit function

\begin{equation} \widetilde{f}(m)=\frac{1}{2}\Vert \scr {J}(m_0)\delta m - d_{{\rm obs}}\Vert _{\scr {D}}^2. \end{equation}

(55)

This problem may be seen as an intermediate between the linearized inversion and FWI. The forward problem is linearized through the ray-Born approximation (Moser 2012); however, the solution is computed in the least-squares sense.

The idea introduced by Jin (1992) is to add a proper scaling in the definition of the associated misfit function, so that the Hessian of this new misfit function should be close from the identity in the asymptotic regime. The scaling acts on the data and corresponds to a weighting function Q(x, x_r, x_s, ω) derived from the one introduced by Beylkin in its definition of the asymptotic inverse of the linearized forward operator. However, since the weighting Q(x, x_r, x_s, ω) depends on the space variable |$x \in \mathbb {R}^{n}$|⁠, the resulting misfit function actually depends on the space variable x. This raises substantial difficulties, as for numerical optimization methods to be used, the misfit function should be positive and scalar-valued.

A new approach is proposed in this study, where we make both numerical and asymptotic approximation collaborating for the model reconstruction, while Jin (1992) and following workers were using only the asymptotic regime for least-squares migration. This approach consists in minimizing the misfit function g(m) defined as

\begin{equation} g(m)=\frac{1}{2}\left\Vert \scr {B}(m_0)\left(d_{{\rm cal}}(m)-d_{{\rm obs}}\right)\right\Vert _{\scr {M}}^2, \end{equation}

(56)

where the integral operator |$\scr {B}(m_0)$| is the Beylkin operator: an asymptotic approximation of the left inverse of J(m₀). Following the Jin's interpretation, the integration of the Beylkin operator may be seen as the definition of particular weights for each triplet source, receiver and frequency, depending on the scattering point which is considered. The final misfit is the integration in space of all these local misfit functions.

The expression for the gradient of g(m) is

\begin{equation} \nabla g(m)=J^{*}(m)\scr {B}(m_0)^{*}\scr {B}(m_0)\left(d_{{\rm cal}}(m)-d_{{\rm obs}}\right). \end{equation}

(57)

Compared to the gradient of the standard misfit function f(m) (eq. 49), the difference induced by the integration of the pre-conditioning operator relies on the multiplication of the residuals by |$\scr {B}(m_0)$| and its adjoint |$\scr {B}(m_0)^{*}$|⁠. These two multiplications can be interpreted as migration and demigration operations on residuals. Indeed, the asymptotic operator of Beylkin is similar to the Born migration operator. This mapping from the data space to the model space is performed following the geodesics defined by rays connecting sources and receivers to the scattering point of the investigated domain. In this work, a unique ray connects each scattering point to each sources and receivers. This is the consequence of the first-arrival assumption. The adjoint operation is a demigration, which is obtained by the application of the adjoint Beylkin operator to a function of the model space. The gradient of the misfit function is thus computed as the correlation between the data generated by localized perturbation in the medium in the single scattering approximation and the residuals obtained after a migration/demigration process. As it is demonstrated in the numerical experiments, this process acts as an illumination angle based filter of the residuals, which emphasizes small illumination angles detrimental to large illumination angles.

The Gauss–Newton approximation of the Hessian of g(m), denoted by |$H^{g}_{{\rm GN}}(m)$|⁠, is

\begin{eqnarray} H^{g}_{{\rm GN}}(m)&=& J^{*}(m)\scr {B}(m_0)^{*}\scr {B}(m_0) J(m)\nonumber\\ &=&\left(\scr {B}(m_0) J(m)\right)^{*}\left(\scr {B}(m_0) J(m)\right). \end{eqnarray}

(58)

From eq. (58), it is clear that the operator |$H^{g}_{{\rm GN}}(m)$| is the normal operator associated with the expression |$\scr {B}(m_0) J(m)$|⁠. In the asymptotic approximation,

\begin{equation} \scr {B}(m_0) J(m)\simeq \scr {B}(m_0) \scr {J}(m). \end{equation}

(59)

In addition, at the first iteration

\begin{equation} \scr {B}(m_0) \scr {J}(m)=\scr {B}(m_0) \scr {J}(m_0). \end{equation}

(60)

In the previous section, following the work of Beylkin, the latter operator has been proved to be a pseudo-differential operator that tends towards the identity as the illumination of the subsurface increases. As a pseudo-differential operator, this property holds for its adjoint. In addition, the composition of two pseudo-differential operators that tends to the identity tends also towards the identity. Therefore, |$H^{g}_{{\rm GN}}(m_0)$| can be approximated as

\begin{eqnarray} H^{g}_{{\rm GN}}(m_0)\simeq \left(\scr {B}(m_0) \scr {J}(m_0)\right)^{*}\left(\scr {B}(m_0) \scr {J}(m_0)\right)\simeq I +\sum _{i} T_i, \nonumber\\ \end{eqnarray}

(61)

where the operators T_i belong to classes of increasingly smooth operators. The introduction of the integral operator |$\scr {B}(m_0)$| in the misfit function thus yields a better conditioned inverse problem, as the Hessian operator associated with the new misfit function should be closer to the identity.

The definition of g(m) given in eq. (56) assumes implicitly that the pre-conditioning operator |$\scr {B}(m_0)$| is computed once for all in the initial model m₀. In fact, one may select a suitable model m_b as the background model where the pre-conditioning operator |$\scr {B}(m_{\rm b})$| is built. Of course, a more elaborate strategy could consist in introducing another non-linearity in g(m) by letting the pre-conditioning operator depend on the current subsurface model m through an updated background model. However, this brings an additional complexity to the problem, not only in terms of computational effort but also in terms of optimization strategy, as the computation of the gradient of g(m) should be modified accordingly. This study is thus restricted to the case where the pre-conditioning operator is computed in the initial model m₀.

4 NUMERICAL STUDY

4.1 Experimental settings and implementation

The aim of the three experiments proposed in this section is to compare standard L² norm-based FWI results with the results obtained when the modified misfit function g(m) introduced in the previous section is used. This comparison is performed in the framework of 2-D acoustic frequency-domain FWI for the reconstruction of the P-wave velocity only. The modelling engine for the solution of the 2-D frequency-domain acoustic equations is based on the mixed-grid finite-difference scheme of Hustedt et al. (2004). The direct solver MUMPS (Amestoy et al.2000) is used to solve the associated linear system. This approach benefits from the efficiency of direct solvers for handling multiple right-hand sides associated with multiple seismic sources.

The optimization scheme which is used to minimize the misfit functions is the l-BFGS algorithm (Nocedal 1980). The choice of this algorithm is made as it only requires the computation of the gradient of the misfit function and shows however improved convergence properties regarding standard steepest descent or non-linear conjugate gradient algorithms. The parameter l sets the number of gradients stored to build the l-BFGS approximation of the inverse Hessian, which is 20 in this study (Nocedal & Wright 2006). The adjoint state method is used to compute the gradient of the misfit functions (Chavent 1974; Plessix 2006). From the implementation point of view, the l-BFGS optimization is performed with the SEISCOPE optimization toolbox, which is interfaced within the code used to achieve these experiments (Métivier & Brossier 2015).

The strategy retained for implementing the asymptotic pre-conditioning strategy consists in computing the Beylkin operator in discrete form off-line. While the first case study is small enough for this operator to be computed explicitly on the same grid as the one used by the finite-difference scheme for the wave propagation modelling, in the second and third case studies (Marmousi2 and Valhall experiments), a compression strategy is applied to reduce the memory requirement and the computation cost. Indeed, there is no need for using a fine sampling to discretize the operator |$\scr {B}(m_0)$|⁠. From its expression in eq. (B17), we see that it is composed of a product of smoothly varying terms multiplied by an oscillatory function. This oscillatory function is an imaginary exponential of the traveltime functions. Again, the traveltime functions are smoothly varying functions, which do not require a fine sampling for an accurate discrete approximation (Thierry et al.1999a; Alkhalifah 2011). This allows to reduce the tremendous memory requirement that would be associated with a discretization of |$\scr {B}(m_0)$| using the fine finite-difference grid of 25 m. In practice, in the second and third case studies, we sample the function |$\scr {B}(m_0)$| with a discretization step |$\tilde{h}$| equal to 100 m both from the model side and the acquisition side, which correspond to a coarsening ratio of 4 in the model dimension and 2 in the acquisition dimension as the original spatial sampling for sources and receivers is equal to 50 m.

4.2 A canonical test case: reconstruction of two inclusions in a smooth background model

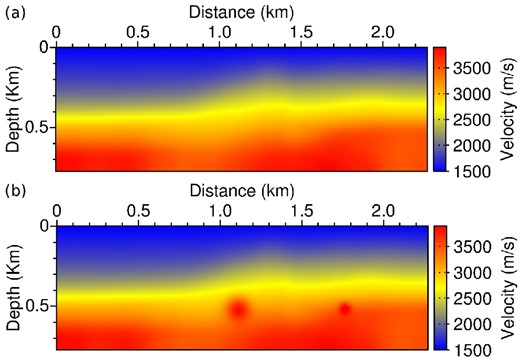
A simple synthetic example is first presented, based on the smooth P-wave background model presented in Fig. 2(a). The domain is 775 m deep and 2275 m wide. Two Gaussian perturbations are added to this model [Fig. 2(b)], centred at the depth z = 500 m. The largest is horizontally centred at x = 1100 m (perturbation 1). The smallest is located on the right at x = 1750 m (perturbation 2). The maximum amplitude of both perturbations is equal to 800 m s⁻¹. A fixed-spread surface acquisition system with 84 sources and receivers, located at the depth z = 50 m, and equally spaced each 25 m, is used. Synthetic data are computed in the perturbed model. A group of 10 frequencies from 3 to 12 Hz with a 1 Hz sampling is used. These synthetic data are inverted using the smooth background model as the initial model m₀. The horizontal and vertical discretization steps for the finite-difference scheme are set to 25 m, which yields a 31 × 91 point discrete model.

Figure 2.

Open in new tab Download slide

Smooth P-wave model used as background model (a). Smooth P-wave model with two Gaussian perturbations added in depth (b).

The experiment starts with the explicit computation of the operators:

\begin{equation} \left\lbrace \begin{array}{l}H_{{\rm GN}}(m_0)=J(m_0)^{*}J(m_0), \\ \scr {B}(m_0) J(m_0), \\ H^{g}_{{\rm GN}}(m_0)=(\scr {B}(m_0) J(m_0))^{*} \scr {B}(m_0)J(m_0). \end{array} \right. \end{equation}

(62)

The following normalization is applied to compare the diagonal dominance pattern of the operators. For a given matrix A, the normalized matrix |$\tilde{A}$| is defined entry wise as

\begin{eqnarray} \forall (i,j), \;\; 1 \le (i,j) \le n, \quad \tilde{A}_{ij}&=&\frac{|A_{ij}|}{\displaystyle ||A||_{\infty }}, \quad \rm { where } \nonumber\\ ||A||_{\infty }&=&\max _{kl} \left|A_{kl}\right|. \end{eqnarray}

(63)

The results are presented in Fig. 3. The refocusing of large-amplitude elements near the diagonal operated by the action of the operator |$\scr {B}(m_0)$| can be clearly observed. While the standard Gauss–Newton operator presents a hardly visible band matrix pattern [Fig. 3(a)], the operator |$\scr {B}(m_0)J(m_0)$| presents a strongly diagonal dominance pattern and appears as a narrow-band matrix [Fig. 3(b)]. The normal matrix associated with this matrix preserves this pattern and is also narrow-band [Fig. 3(c)].

Figure 3.

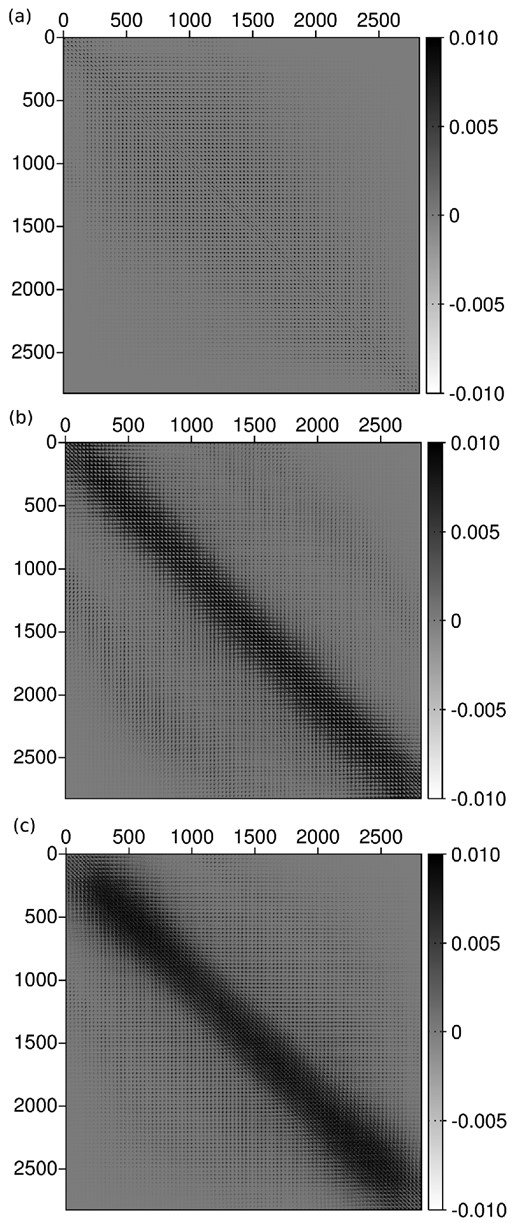
$Rescaled operators. Gauss–Newton operator HGN(m0) associated with the standard FWI misfit function (a), product of the Beylkin and the Born modelling operators $\scr {B}(m_0)J(m_0)$ (b), Gauss–Newton operator $H_{{\rm GN}}^{g}(m_0)$ (c).$

Open in new tab Download slide

Rescaled operators. Gauss–Newton operator H_GN(m₀) associated with the standard FWI misfit function (a), product of the Beylkin and the Born modelling operators |$\scr {B}(m_0)J(m_0)$| (b), Gauss–Newton operator |$H_{{\rm GN}}^{g}(m_0)$| (c).

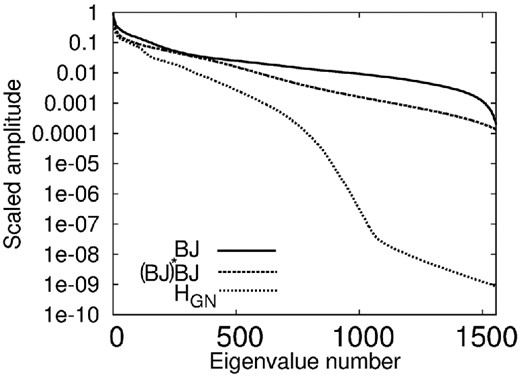
To complement the analysis of these operators, the distribution of their eigenvalues is presented in Fig. 4. The spectrum of the standard Gauss–Newton operator presents a rapid decrease after the 200th eigenvalue. In contrast, the spectrum of the operator |$\scr {B}(m_0)J(m_0)$| and its associated normal operator |$H^{g}_{GN}(m_0)$| presents a slower decrease. This indicates the better conditioning of these operators compared to the standard Gauss–Newton operator.

Figure 4.

$Eigenvalue distribution of the Gauss–Newton operator associated with the standard FWI misfit function HGN(m0), the product of the Beylkin and the Born modelling operators $\scr {B}(m_0)J(m_0)$, the Gauss–Newton operator $H_{{\rm GN}}^{g}(m_0)=\left(\scr {B}(m_0)J(m_0)\right)^{*}\scr {B}(m_0)J(m_0)$ associated with the modified misfit function g(m).$

Open in new tab Download slide

Eigenvalue distribution of the Gauss–Newton operator associated with the standard FWI misfit function H_GN(m₀), the product of the Beylkin and the Born modelling operators |$\scr {B}(m_0)J(m_0)$|⁠, the Gauss–Newton operator |$H_{{\rm GN}}^{g}(m_0)=\left(\scr {B}(m_0)J(m_0)\right)^{*}\scr {B}(m_0)J(m_0)$| associated with the modified misfit function g(m).

The right most perturbation introduced in the background model is smaller in size than the other and is not centred with respect to the acquisition system. Therefore, its imprint in the data should be significantly smaller than the imprint of the largest perturbation. It is thus expected that, in the first iterations, the L² norm-based gradient focusses mainly on the first perturbation and neglects the second perturbation. The modification of the misfit function through the Beylkin operator should balance this focusing. The projection of the residuals in the model space should allow to give more emphasis to the data associated with the smaller perturbation. It is thus expected that the gradient of the modified misfit function g(m) provides an update accounting for the two perturbations. As discussed in the previous section, the modification of the misfit function amounts to only modifying the computation of the data residuals. In Fig. 5, the standard L² norm residuals,

\begin{equation} d_{{\rm obs}}(x_{\rm r},x_{\rm s},\omega )-d_{{\rm cal}}(x_{\rm r},x_{\rm s},\omega ), \end{equation}

(64)

are compared with the migrated/demigrated residuals,

\begin{equation} \scr {B}(m_0)^{*}\scr {B}(m_0)\left(d_{{\rm obs}}(x_{\rm r},x_{\rm s},\omega )-d_{{\rm cal}}(x_{\rm r},x_{\rm s},\omega )\right). \end{equation}

(65)

Fig. 5 is organized by frequencies: the 10 panels correspond to the 10 different frequencies from 3 to 12 Hz. Each panel is a presentation of the real part of the residuals in the frequency domain in the receiver/source plane. The top panels [Fig. 5(a)] present the residuals associated with the standard L² norm, while the bottom panels [Fig. 5(b)] present the residuals after migration/demigration. For the L² norm, at low frequency, the residuals seem to be associated only with the first inclusion. The imprint of the second inclusion is present only at higher frequencies, from 9 to 12 Hz. Along all the bandwidth, signals associated with receivers and sources at a larger distance from the targets are also visible. These signals correspond to larger offset data recorded by the acquisition system.

Figure 5.

Residuals in the source/receiver plane, for the 10 different frequencies from 3 to 12 Hz. L2 norm-based standard residuals (a). Migrated/Demigrated residuals (b).

Open in new tab Download slide

Residuals in the source/receiver plane, for the 10 different frequencies from 3 to 12 Hz. L² norm-based standard residuals (a). Migrated/Demigrated residuals (b).

In contrast, the imprint of the two inclusions is clearly visible in the residuals associated with the modified misfit function g(m) from lower frequencies. Already at 4 Hz, the effect of the second inclusion is visible in the residuals. Another difference is that the long-offset residuals are filtered. The migration/demigration operation results in an emphasis on the information associated with near-offset data. The illumination angle filtering resulting from the application of the operator |$\scr {B}(m_0)^{*}\scr {B}(m_0)$| to the data residuals can be related to the mathematical definition of the Beylkin operator and its adjoint, given in Appendix B. From the formulas (B17) and (B18), it can be seen that a multiplication by a factor (cos (θ) + 1)² is applied to each residual components, which implies the observed emphasis of small illumination angles.

The gradients associated with the standard L² norm-based misfit function and the modified misfit function are presented in Fig. 6. For a fair comparison, the same scaling is applied to both of the gradients. As expected, the L² norm-based gradient [Fig. 6(a)] mainly focusses on the first inclusion, which is centred with respect to the acquisition system, and is larger in size. In contrast, the gradient of the modified misfit function provides a more balanced update for the large and small inclusions [Fig. 6(b)]. On the other hand, positive/negative oscillations around the inclusions are introduced, which resembles limited bandwidth effects observed in the reconstruction provided by asymptotic linearized inverse methods [see for instance Thierry et al. (1999a)]. The balance in the inclusion reconstruction and these oscillations are the imprint of the introduction of the Beylkin operator in the misfit function.

Figure 6.

Gradients computed for the two inclusions case study. Standard L2 norm-based gradient (a). Modified misfit function gradient ∇g(m) (b).

Open in new tab Download slide

Gradients computed for the two inclusions case study. Standard L² norm-based gradient (a). Modified misfit function gradient ∇g(m) (b).

4.3 Application to the Marmousi model

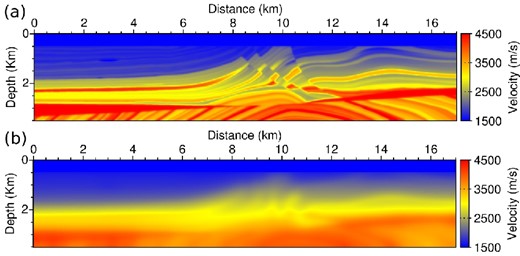
The properties of the modified misfit function are analysed on the acoustic Marmousi2 model (Martin et al.2006). The exact and initial models are presented in Fig. 7. The domain size is 3 km deep and 17 km wide. The initial model is obtained by a Gaussian smoothing of the exact model with a correlation length equal to 375 m. This yields an accurate initial model. A fixed-spread surface acquisition system with 336 sources and receivers located at 50 m depth and spread along the upper water layer from x = 0.15 km to x = 16.9 km each 50 m is used. The frequency bandwidth for the data goes from 3 to 7.5 Hz. The P-wave velocity in the water layer is supposed to be known. It is kept constant, equal to 1500 m s⁻¹, throughout the inversion process. The spatial discretization h for the finite-difference scheme is set to 25 m both in vertical and horizontal directions, which yields a 141 × 681 point discrete model. As mentioned preliminary, the operator |$\scr {B}(m_0)$| is discretized over a coarse grid with a discretization step |$\tilde{h}=100$| m. A fine frequency discretization is used, with a sampling of 0.25 Hz, which yields a data set with 19 discrete frequencies from 3 to 7.5 Hz. Numerical experiments presented in the sequel show that this fine discretization is required for the asymptotic pre-conditioning to be accurate.

Figure 7.

Open in new tab Download slide

Marmousi 2 P-wave exact (a) and initial (b) models.

The standard L² norm residuals are compared with the migrated/demigrated residuals for five frequencies (3, 4, 5, 6 and 7 Hz) in Fig. 8. As in the previous experiment, for each frequency, a panel presents the real part of the residuals in the source/receiver plane. The migration/demigration process operates a strong filtering of the residuals associated with long-offset data and focusses on near-offset data. This is again the impact of the angle illumination filtering associated with the Beylkin operator. This may result in emphasizing reflection data at the expense of diving-wave data.

Figure 8.

Marmousi2 case study. Normalized residuals for the frequencies 3, 4, 5, 6 and 7 Hz. Standard L2 norm-based residuals (a) and migrated/demigrated residuals (b).

Open in new tab Download slide

Marmousi2 case study. Normalized residuals for the frequencies 3, 4, 5, 6 and 7 Hz. Standard L² norm-based residuals (a) and migrated/demigrated residuals (b).

In Fig. 9, the model update provided by the solution of the linearized inversion problem following the Beylkin strategy

\begin{equation} \delta m=\scr {B}(m_0)\left(d_{{\rm cal}}(m_0)-d_{{\rm obs}}\right) \end{equation}

(66)

is compared with the gradient in the initial model of the standard FWI misfit and the modified misfit introduced in this study. Spatial aliasing corrupts the update δm. This is due to the sampling of |$\scr {B}(m_0)$| on the coarse grid. However, it is still visible that δm is a migration result, with clearly delineated interfaces, in shallow and deep parts of the model. The main structure of the exact model appears. The gradient provided by standard FWI only focusses on smooth updates of the shallow part. No modification is provided deeper than 2 km. This gradient is driven by diving-wave data that sample the shallow part of the model and provide long-wavelength updates of the model. In contrast, the gradient associated with the modified misfit function resembles strongly the model update δm. However, the spatial aliasing is removed, and the amplitudes are balanced between shallow and deep parts of the model. In addition, a smooth, low-wavenumber correction is provided in the shallow zone between z = 0.5 km, z = 1.5 km and x = 1, x = 6 km. The gradient of the modified misfit function thus seems to be mainly based on the model update δm but also incorporates information resembling the one provided by standard FWI, through the fact that the calculated data in the residuals are computed with a full two-way wave equation rather than with the linear ray+Born approximation.

Figure 9.

$Model update $\scr {B}(m_0)(d_{{\rm cal}}(m_0)-d_{{\rm obs}})$ which would be provided by the Beylkin method (a), standard FWI gradient in the initial Marmousi 2 model (b) and modified misfit function gradient in the initial Marmousi 2 model ∇g(m0) (c).$

Open in new tab Download slide

Model update |$\scr {B}(m_0)(d_{{\rm cal}}(m_0)-d_{{\rm obs}})$| which would be provided by the Beylkin method (a), standard FWI gradient in the initial Marmousi 2 model (b) and modified misfit function gradient in the initial Marmousi 2 model ∇g(m₀) (c).

The effect of the frequency sampling on the accuracy of the Beylkin operator |$\scr {B}(m_0)$| is presented in Fig. 10. Coarsening the frequency sampling to 0.5 and 1 Hz yields important artefacts on the gradient of the modified misfit function g(m). This effect is consistent with the formulas (42) and (43). The asymptotic convergence of |$\scr {B}(m_0)$| towards a left inverse of J(m₀) requires the domain of integration in frequency to go continuously from 0 towards the infinity. Approximating this integral with a too coarse frequency sampling decreases the accuracy of the approximation.

Figure 10.

Open in new tab Download slide

Marmousi2 case study. Effect of the frequency sampling. Gradient of the modified misfit function g(m) with 1, 0.5 and 0.25 Hz samplings.

The effect of the compression used to compute the Beylkin operator |$\scr {B}(m_0)$| is also presented in Fig. 11. Not surprisingly, if the operator is approximated on a too coarse grid in space, spatial aliasing will not be totally removed in the gradient of the modified misfit function g(m). The coarsening which is used should be actually chosen consistently with the expected resolution. Here, as the frequency content of the data does not exceed 7.5 Hz, a spatial discretization of 100 m is enough for obtaining a smooth P-wave velocity gradient.

Figure 11.

$Marmousi2 case study. Effect of the compression level used for computing the Beylkin operator $\scr {B}(m_0)$. Gradient of the modified misfit function g(m) with 400, 200 and 100 m grids.$

Open in new tab Download slide

Marmousi2 case study. Effect of the compression level used for computing the Beylkin operator |$\scr {B}(m_0)$|⁠. Gradient of the modified misfit function g(m) with 400, 200 and 100 m grids.

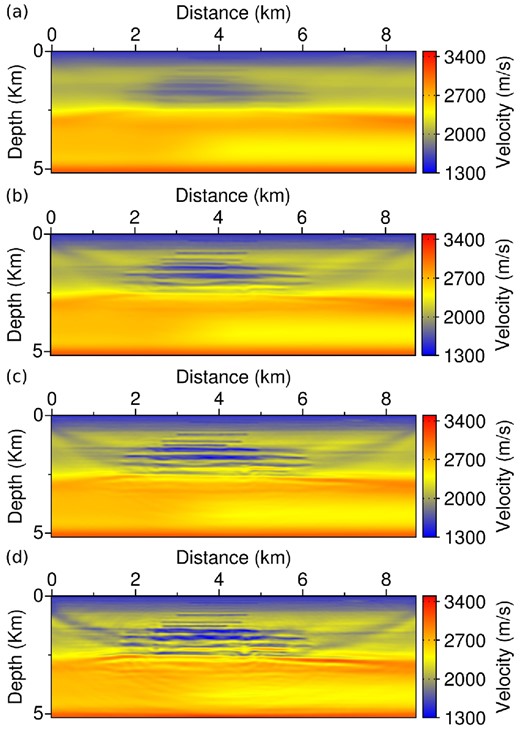
The inversion results obtained with the modified misfit function after 3 and 10 l-BFGS iterations are presented in Fig. 12. These results have to be compared with those obtained using the standard L² norm after 3, 10 and 40 l-BFGS iterations, presented in Fig. 13. A diagonal pre-conditioning based on the pseudo-Hessian operator is included in the l-BFGS algorithm for the standard FWI method (Shin et al.2001). Details on practical implementation of this pre-conditioning strategy can be found in Métivier & Brossier (2015).

Figure 12.

Open in new tab Download slide

Marmousi2 case study. Reconstructed models after 3 (a) and 10 (b) l-BFGS iterations using the modified misfit function g(m).

Figure 13.

Open in new tab Download slide

Marmousi2 case study. Reconstructed models after 3 (a), 10 (b) and 40 (c) l-BFGS iterations using standard FWI with a diagonal pre-conditioner.

While in standard FWI the estimation first focusses on the shallow part and progressively reconstructs the deeper parts of the model, the modification introduced by the Beylkin operator allows to reconstruct deep structures in the very first iterations. This is due to the focusing of the method on smaller illumination angles and reflection data. A high-resolution estimation of the subsurface model is yielded directly in the first iterations. The progress between the third and the tenth iterations indicates a reconstruction of amplitudes rather than the building of interfaces. As a counterpart, the shallow part of the model, sampled both by diving and reflected waves, is less constrained when using the modified misfit function. The estimation in this zone is less accurate than the ones obtained with a standard FWI method. This seems a limitation of the approach, caused by the filter applied to diving waves induced by the asymptotic operator.

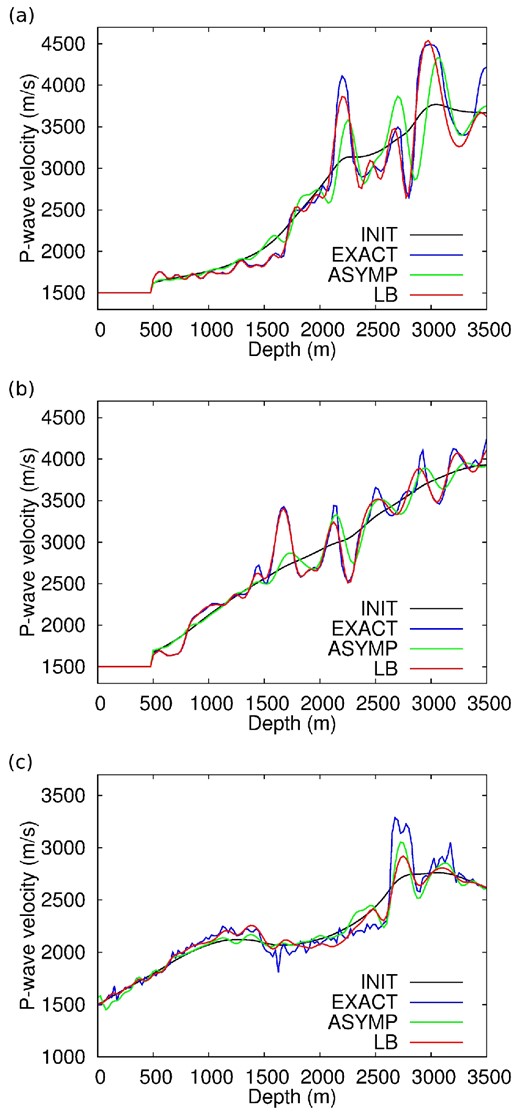
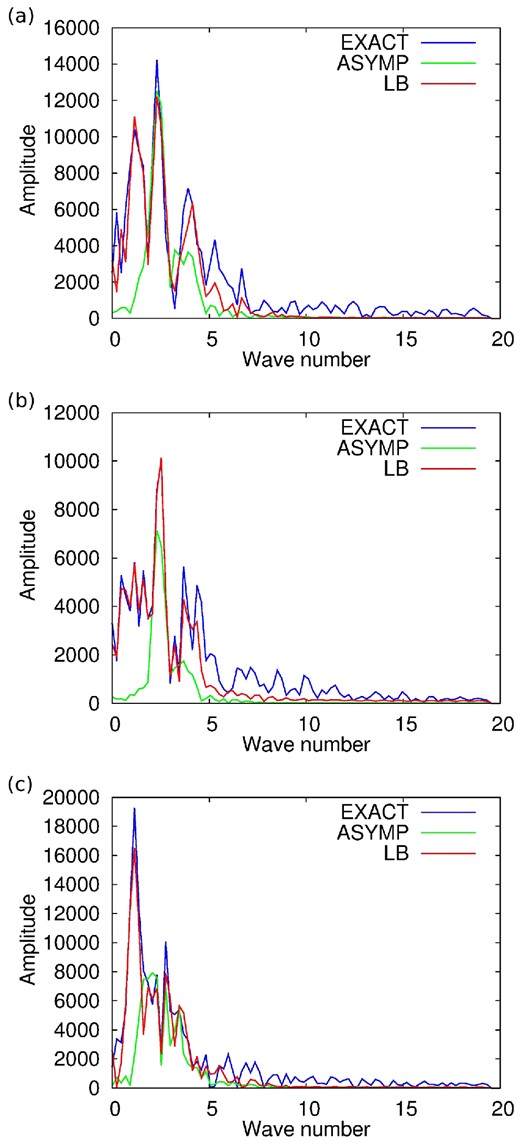
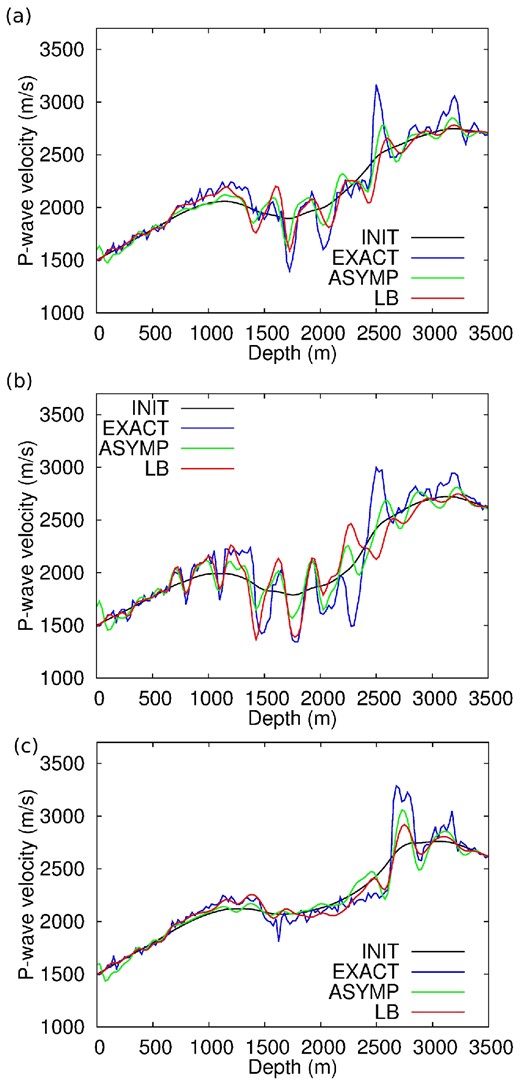
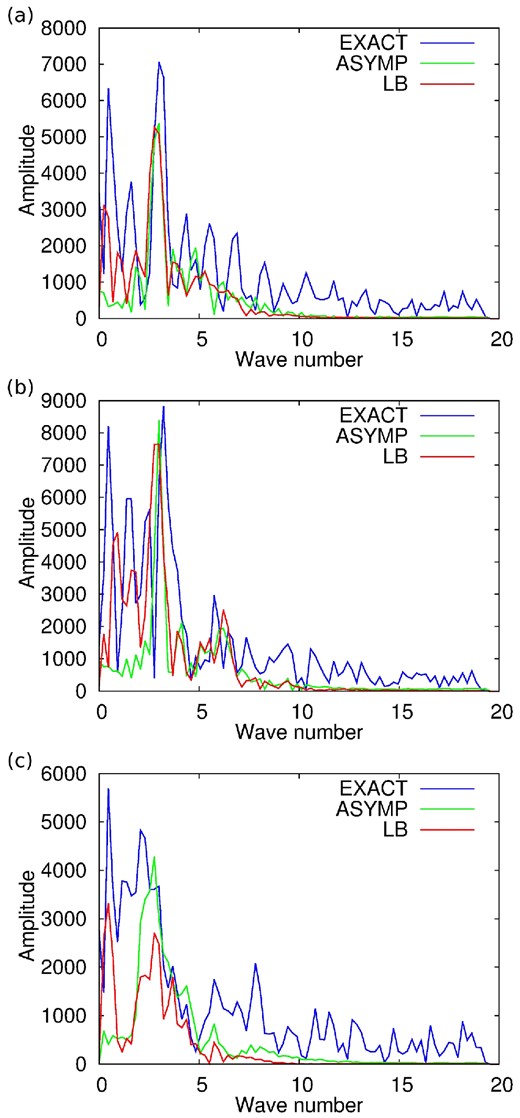
To further investigate this issue, vertical P-wave velocity profiles are presented in Fig. 14. Theses profiles are taken at x = 5 km, x = 9 km and x = 14 km, respectively. The profiles obtained after 40 iterations of pre-conditioned l-BFGS follow almost exactly the exact profiles, excepted in depth, where the true amplitude of the reflectors is not recovered. The results obtained after 10 l-BFGS iterations using the modified misfit function show that the trend is recovered both in shallow and deep parts around the initial model profile. This suggests that the low-frequency part of the model is not updated. The reflectors are thus located at their proper locations, but a lack of low-wavenumber updates is visible. This analysis is confirmed in Fig. 15 where the frequency content of the vertical profiles is presented. The profiles obtained from 40 iterations of pre-conditioned l-BFGS recover the low-frequency part of the exact profiles. The profiles obtained after 10 iterations of l-BFGS using the modified misfit function clearly present a gap in the low-wavenumber part of the spectrum.

Figure 14.

Open in new tab Download slide

Marmousi2 case study. Vertical logs of P-wave velocity models extracted at x = 5 km (a), x = 9 km (b) and x = 14 km (c). Exact model (red), initial model (black), reconstructed model after 10 iterations of modified FWI (green) and reconstructed model after 40 iterations of standard FWI (blue).

Figure 15.

Open in new tab Download slide

Marmousi2 case study. Wavenumber spectrum of the P-wave velocity update along vertical logs extracted at x = 5 km (a), x = 9 km (b) and x = 14 km (c). Exact update (blue), update obtained after 10 iterations of modified FWI (green) and update obtained after 40 iterations of standard FWI (red).

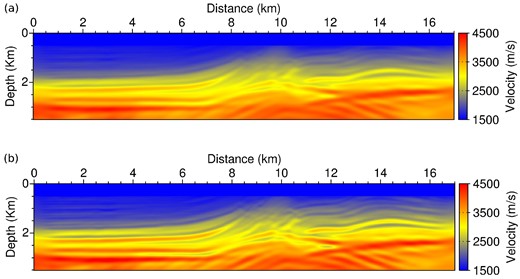
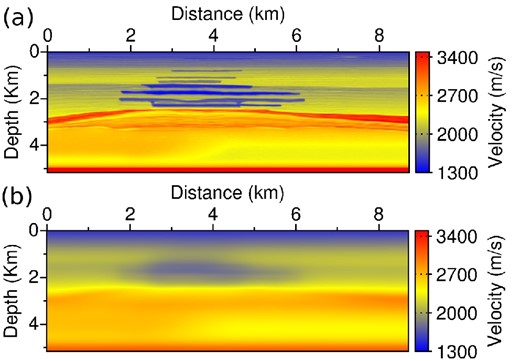
4.4 Application to the synthetic Valhall model

The numerical experiments are completed by an application on the synthetic Valhall model presented in Fig. 16, together with the initial model which is used. The model is deeper than the Marmousi 2 model; its lateral extension is smaller: it is 5 km deep and 8.7 km wide. It presents interesting low-velocity layers associated with the presence of gas and a strong curved reflector located above z = 3 km. As in the Marmousi 2 experiment, a fixed-spread surface acquisition system is used with 173 sources and receivers located at 50 m depth and spread along the horizontal axis from x = 0 km to x = 8.65 km each 50 m. The frequency bandwidth for the data goes from 3 to 7 Hz. The frequency sampling is equal to 0.25 Hz, as in the Marmousi 2 experiment, which yields a data set with 17 discrete frequencies. The spatial discretization h is set to 25 m both in vertical and horizontal directions, which yields a 207 × 349 point discrete model. Compared to the Marmousi2 case study, the reduction of the maximum offset of the acquisition system and the good quality of the initial velocity model emphasize the importance of reflected waves rather than diving waves for recovering the exact P-wave velocity model. It is expected that in this situation, the approach based on the modified misfit function g(m) provides good results.

Figure 16.

Open in new tab Download slide

Exact (a) and initial (b) models for the Valhall case study.

In Fig. 17, the residuals associated with the standard L² norm-based FWI are compared to the residuals after migration and demigration using the Beylkin operator |$\scr {B}(m_0)$| and its adjoint. The same presentation as for the previous case studies is used: the five panels are associated with the frequencies 3, 4, 5, 6 and 7 Hz. Each panel is a presentation of the residuals in the source/receiver plane. The migration/demigration operation focusses again on near-offset data, detrimental to far-offset data.

Figure 17.

Normalized residuals for the frequencies 3, 4, 5, 6 and 7 Hz. Standard L2 norm-based residuals (a) and migrated/demigrated residuals (b).

Open in new tab Download slide

Normalized residuals for the frequencies 3, 4, 5, 6 and 7 Hz. Standard L² norm-based residuals (a) and migrated/demigrated residuals (b).

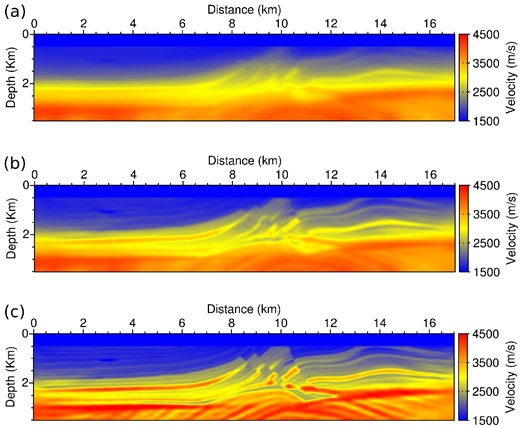
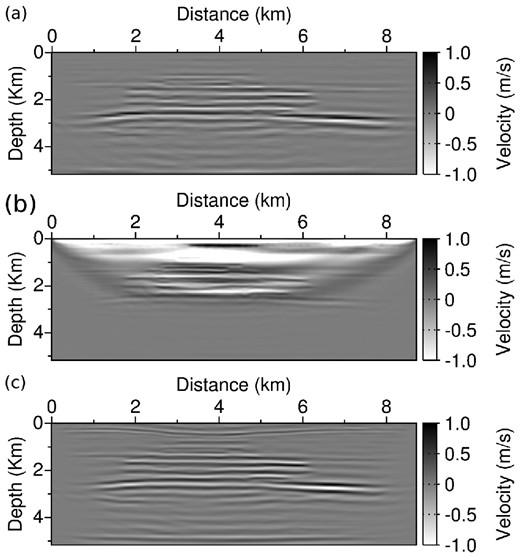
In Fig. 18, the model update δm associated with the Beylkin migration (eq. 66) is compared to the gradient in the initial model associated with the standard FWI misfit function and the modified misfit function. As a migration result, the model update δm [Fig. 18(a)] yields a good reconstruction of the interfaces present in the exact velocity model presented in Fig. 16. Because of the coarse sampling of |$\scr {B}(m_0)$|⁠, the update suffers from spatial aliasing, although this is less visible than in the Marmousi 2 experiment. The FWI gradient [Fig. 18(b)] focusses mainly on the shallow part of the model. A smooth, low-wavenumber update of the zone above the first kilometre is provided, associated with transmitted energy. Two dark wings also appear connecting both lateral extremities of the acquisition to the zone in the centre. These artefacts are due to the incompleteness of the acquisition. The modified misfit gradient [Fig. 18(c)] appears as a smoother version of δm. The spatial aliasing effect is removed. The amplitude of the model update is corrected. A very shallow reflector at z = 0.5 km also appears, which is not visible in δm.

Figure 18.

$Model update $\scr {B}(m_0)(d_{{\rm cal}}(m_0)-d_{{\rm obs}})$ which would be provided by the Beylkin method (a), standard FWI gradient in the initial Valhall model (b) and gradient of the modified misfit function g(m) in the initial Valhall model (c).$

Open in new tab Download slide

Model update |$\scr {B}(m_0)(d_{{\rm cal}}(m_0)-d_{{\rm obs}})$| which would be provided by the Beylkin method (a), standard FWI gradient in the initial Valhall model (b) and gradient of the modified misfit function g(m) in the initial Valhall model (c).

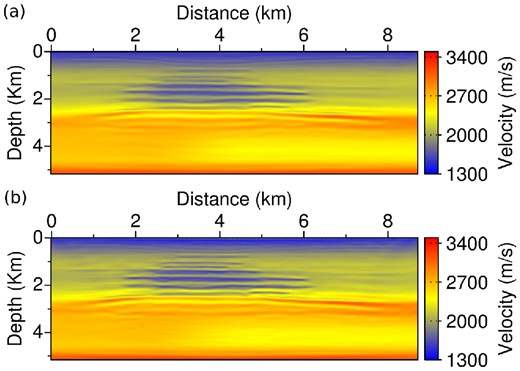
The results obtained after 5 and 10 l-BFGS iterations using the modified misfit function g(m) are presented in Fig. 19. After five iterations, the main interfaces already appear clearly in the estimated model. The gas layers are accurately reconstructed. The main reflector at z = 3 km is well delineated from x = 1 km to x = 7 km. Additional iterations (from 5 to 10) allow to restore more accurately the amplitude and to improve slightly the resolution of the estimation. The results obtained after 5, 10 and 20 l-BFGS iterations using the standard FWI misfit function with a diagonal pre-conditioning strategy are presented in Fig. 20. At least 20 iterations are required for the standard FWI method to be able to reconstruct satisfactorily the gas layers in the middle of the domain [Fig. 20(d)]. However, the deepest part of the model, including the main reflector at z = 3 km, is less precisely estimated in this case. In comparison, this reflector is more accurately estimated when the modified misfit function g(m) is used. Here, the standard FWI method faces an important difficulty as increasing the number of iteration does not seem to improve further the solution. After 40 iterations, the main reflector appears more clearly only between x = 1 km, x = 2 km and x = 5 km, x = 7 km. The reconstruction of the gas layers starts to reveal some instabilities, despite the synthetic data are not corrupted by any noise. Note for instance the high-amplitude artefact appearing in red at z = 2.5 km, x = 5 km [Fig. 20(e)]. This instability is not observed when the modified misfit function g(m) is used.

Figure 19.

Open in new tab Download slide

Reconstructed model after 5 (a) and 10 (b) l-BFGS iterations using the modified misfit function g(m).

Figure 20.

Open in new tab Download slide

Reconstructed model after 5 (a), 10 (b), 20 (c) and 40 (d) l-BFGS iterations using standard FWI with a diagonal pre-conditioner.

To complement this analysis, P-wave velocity vertical profiles of the reconstructed models are presented in Fig. 21. The profiles are extracted at x = 2.1 km, x = 4.4 km and x = 6.5 km. The reconstructed models obtained after 10 l-BFGS iterations using the modified misfit function g(m) and 20 l-BFGS iterations using standard FWI with a diagonal pre-conditioning are compared to the exact and the initial models. For the three logs, the model reconstructed using the modified misfit function is the closest to the exact profile, especially in depth (z > 2 km). This is consistent with the observations made on the 2-D reconstructions. However, as for the Marmousi2 case study, the updates obtained using the modified misfit function seems to lack low-wavenumber content. This observation is supported by the 1-D spectral analysis of these updates presented in Fig. 22.

Figure 21.

Open in new tab Download slide

Valhall case study. Vertical logs of P-wave velocity models extracted at x = 2.1 km (a), x = 4.4 km (b) and x = 6.2 km (c). Exact model (blue), initial model (black), reconstructed model after 10 iterations of modified FWI (green) and reconstructed model after 40 iterations of standard FWI (red).

Figure 22.

Open in new tab Download slide

Valhall case study. Wavenumber spectrum of the P-wave velocity update along vertical logs extracted at x = 2.1 km (a), x = 4.4 km (b) and x = 6.2 km (c). Exact model (red), initial model (black), reconstructed model after 10 iterations of modified FWI (green) and reconstructed model after 40 iterations of standard FWI (blue).

5 DISCUSSION

The results presented in this study provide important information. First, it should be noted that despite working with FWI far from the high-frequency regime, with a seismic data bandwidth comprised between 3 and 7.5 Hz, the asymptotic approximation still brings valuable information on the propagation operators involved in the inversion process. In particular, the left inverse devised by Beylkin from the asymptotic approximation of the Born modelling operator is still a relatively good left pre-conditioner for the ‘true’ Born modelling operator, computed with the full wavefield. This is emphasized in the first case study, where these operators are presented (Fig. 3). This result indicates that the asymptotic approximation is meaningful and could be used to build pre-conditioners even far from the high-frequency regime.

Second, introducing the Beylkin operator within the FWI scheme through the definition of the modified misfit function (56) is not without having some consequences on the inversion process. The filtering applied on the data residuals associated with wide scattering angles should be underlined. The method amounts to significantly focus on the short-offset data rather than long-offset data, as can be seen in the migrated/demigrated residuals in Figs 5, 8 and 17. This makes the method similar to a migration process rather than a full waveform inversion process as long-offset data maybe not accounted for accurately.

Let us recall the expression of the modulus of the reconstructed wavenumber model |k| in the context of diffraction tomography (Devaney 1982),

\begin{equation} |k(x)|=\frac{2 f\cos \left(\theta (x)/2\right)}{c(x)}, \end{equation}

(67)

where θ is the illumination angle, f the dominant frequency of the data and c(x) the local velocity. This equation shows that the loss of sensitivity to long-offset data decreases the capability of the method to retrieve low-wavenumber components of the P-wave velocity model.

From the expression of the Beylkin operator, one could think, however, that this effect is counterbalanced by the frequency weighting strategy embedded in this operator. Indeed, from eq. (B17), one can see that a scaling factor equal to the inverse of the frequency is applied to the data, which gives more weight to low-frequency data rather than higher frequency data in the inversion. This makes possible to enhance the reconstruction of low-wavenumber components of the P-wave velocity model, according to the expression (67). This strategy, named as spectral shaping, is presented in Lazaratos et al. (2011) and Plessix (2013). However, the numerical results presented here tend to indicate that the compensation induced by this frequency weighting is not sufficient: the illumination angle based filtering has a stronger influence on the reconstruction process.

Nevertheless, if the low-wavenumber components of the solution is contained in the initial model, it appears that the modification of the misfit function improves significantly the convergence speed of the minimization process. This suggests that the modified misfit function could be used for instance for accelerating non-linear quantitative migration algorithms, such as in Métivier et al. (2011) and Métivier (2011) for the reconstruction of the acoustic impedance around a well with walkaway data, with a given velocity model. In Zhou et al. (2014a,b), a method is proposed for the coupled reconstruction of the low-wavenumber components of the P-wave velocity model and the high-wavenumber components of the P-impedance. At each iteration of the process, a non-linear minimization has to be performed to compute the reflectivity model with the current velocity model: the method proposed here could also be applied to accelerate this process.

In terms of practical implementation, the computation of the Beylkin operator amounts to the computation of a large-scale dense matrix. This requires a significant computational effort and has a strong impact on its memory requirement. A coarsening strategy has to be applied in accordance with the frequency content of the data which is inverted. Practicing an off-line computation of the operator as a prior stage to the inversion reduces the computational cost as the quantities from the Beylkin operator are computed only once. As a counterpart, this requires the ability of storing the dense matrix on the coarse grid. A trade-off could be found by recomputing some of the matrix entries at each iteration. Another possibility also consists in using compression strategies, such as the ACA method to devise H-matrix approximation of the Beylkin operator (Bebendorf 2008).

Finally, the approach is presented here in the frequency domain for the sake of simplicity. However, the strategy can be extended to time-domain inversion. In the work of Beylkin (1985), the derivation of the migration operator was initially performed in the time domain. In practice, the frequency-domain inversion requires a fine sampling of the frequency integration domain (see Fig. 10). The computational gain associated with frequency-domain approach for FWI relies on the possibility of exploiting data redundancy and invert for few discrete frequencies. Therefore, in this case, it seems that there are no advantages to keep a frequency-domain approach. The method could thus be considered for accelerating the convergence of time-domain least-squares migration algorithms, which are known to be intensively time consuming.

6 CONCLUSION

This study presents a strategy for combining concepts inherited from linearized inversion with non-linear least-squares inversion scheme such as FWI. In particular, the preserved-amplitude migration operator derived by Beylkin (1985) from the adjoint of the asymptotic approximation of the Born modelling operator is used to define a modified misfit function. The gradient associated with this new misfit function shares some similarities with the standard L² norm-based FWI gradient. It is the cross-correlation of the wavefield diffracted by any single localized perturbation of the discrete medium with residuals. The difference with standard FWI is that the residuals on which the method applies are first migrated/demigrated using the Beylkin operator and its adjoint. The Hessian of this modified misfit function is shown to tend asymptotically towards the identity operator. As an inverse problem, the minimization of this misfit function is thus a better posed problem, as the trade-off between parameters is reduced.

It is observed numerically that despite working far from the high-frequency regime, the modified misfit function has indeed a diagonal dominant Hessian operator. However, the modification of the misfit function through the Beylkin operator implies a focussing of the method on small illumination angle data, detrimental to large-offset data. As a consequence, the sensitivity of the misfit function to diving waves is reduced, and the method is efficient only in a migration regime. This indicates that this strategy could be employed for accelerating non-linear quantitative migration algorithms.

The results which have been obtained suggests that the asymptotic approximation should be an appropriate tool to better condition the FWI problem. Future studies will be led to investigate the use of the Beylkin operator for building directly an approximate inverse of the Hessian operator. This pre-conditioner could be used in the framework of a truncated Newton method. This strategy is expected to be efficient especially for the multiparameter case for which trade-offs between different classes of parameters (for instance P-wave velocity and density in the acoustic approximation) make the computation of a decoupled estimation a strongly difficult task.

It is important to emphasize that the asymptotic approximation can be extended to account for anisotropy, attenuation and the propagation of elastic waves. Extension to multi-arrival can also be performed to improve the accuracy and the impact of an asymptotic pre-conditioning. Therefore, the approach which is developed here is not limited to the acoustic case and is hopefully a preliminary step towards the definition of more general pre-conditioners for FWI.

This study was partially funded by the SEISCOPE consortium (http://seiscope2.osug.fr), sponsored by BP, CGG, CHEVRON, EXXON-MOBIL, JGI, PETROBRAS, SAUDI ARAMCO, SCHLUMBERGER, SHELL, SINOPEC, STATOIL, TOTAL and WOODSIDE. This study was granted access to the HPC resources of the Froggy platform of the CIMENT infrastructure (https://ciment.ujf-grenoble.fr), which is supported by the Rhône-Alpes region (GRANT CPER07_13 CIRA), the OSUG@2020 labex (reference ANR10 LABX56) and the Equip@Meso project (reference ANR-10-EQPX-29-01) of the programme Investissements d'Avenir supervised by the Agence Nationale pour la Recherche, and the HPC resources of CINES/IDRIS under the allocation 046091 made by GENCI. The authors thank all the actors of the SEISCOPE consortium research group for their active and constant support, especially Stéphane Operto for helpful and animated discussions.

REFERENCES

Alkhalifah

T.

.

Efficient traveltime compression for 3D prestack kirchhoff migration

,

Geophys. Prospect.

,

2011

, vol.

59

(pg.

1

-

9

)

Alkhalifah

T.

,

Plessix

R.

.

A recipe for practical full-waveform inversion in anisotropic media: an analytical parameter resolution study

,

Geophysics

,

2014

, vol.

79

3

(pg.

R91

-

R101

)

Amestoy

P.

,

Duff

I.S.

,

L'Excellent

J.Y.

.

Multifrontal parallel distributed symmetric and unsymmetric solvers

,

Computer Methods in Applied Mechanics and Engineering

,

2000

, vol.

184

2-4

(pg.

501

-

520

)

Bebendorf

M.

. ,

Hierarchical Matrices: A Means to Efficiently Solve Elliptic Boundary Value Problems (Lecture Notes in Computational Science and Engineering)

,

2008

1st edn

Springer

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Beylkin

G.

.

Imaging of discontinuities in the inverse scattering problem by inversion of a causal generalized Radon transform

,

J. Math. Phys.

,

1985

, vol.

26

(pg.

99

-

108

)

Beylkin

G.

.

Bernabini

M.

,

Carrion

P.

,

Jacovitti

G.

,

Rocca

F.

,

Treitel

S.

,

Worthington

M.

.

Mathematical theory for seismic migration and spatial resolution

,

Deconvolution and Inversion

,

1987

Blackwell Scientific Publications

(pg.

291

-

304

)

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Beylkin

G.

,

Burridge

R.

.

Linearized inverse scattering problems in acoustics and elasticity

,

Wave motion

,

1990

, vol.

12

(pg.

15

-

52

)

Bleistein

N.

.

On the imaging of reflectors in the Earth

,

Geophysics

,

1987

, vol.

52

7

(pg.

931

-

942

)

Bleistein

N.

,

Cohen

J.K.

,

Hagin

F.G.

.

Computational and asymptotic aspects of velocity inversion

,

Geophysics

,

1985

, vol.

50

8

(pg.

1253

-

1265

)

Bonnans

J.F.

,

Gilbert

J.C.

,

Lemaréchal

C.

,

Sagastizábal

C.A.

. ,

Numerical Optimization, Theoretical and Practical Aspects

,

2006

Springer Series, Universitext

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Brossier

R.

,

Operto

S.

,

Virieux

J.

.

Seismic imaging of complex onshore structures by 2D elastic frequency-domain full-waveform inversion

,

Geophysics

,

2009

, vol.

74

6

(pg.

WCC105

-

WCC118

)

Castellanos

C.

,

Métivier

L.

,

Operto

S.

,

Brossier

R.

,

Virieux

J.

.

Fast full waveform inversion with source encoding and second-order optimization methods

,

Geophys. J. Int.

,

2015

, vol.

200

2

(pg.

720

-

744

)

Chavent

G.

.

Goodson

R.

,

Polis

M.

.

Identification of parameter distributed systems

,

Identification of Function Parameters in Partial Differential Equations

,

1974

American Society of Mechanical Engineers

(pg.

31

-

48

)

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Devaney

A.J.

.

A filtered backprojection algorithm for diffraction tomography

,

Ultrasonic Imaging

,

1982

, vol.

4

(pg.

336

-

350

)

Fichtner

A.

,

Kennett

B.L.N.

,

Igel

H.

,

Bunge

H.P.

.

Theoretical background for continental- and global-scale full-waveform inversion in the time-frequency fomain

,

Geophys. J. Int.

,

2008

, vol.

175

(pg.

665

-

685

)

Forgues

E.

.

Inversion linearisée multi-paramètres via la théorie des rais

,

PhD thesis

,

1996

Institut Français du Pétrole - University Paris VII

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Gao

F.

,

Levander

A.R.

,

Pratt

R.G.

,

Zelt

C.A.

,

Fradelizio

G.L.

.

Waveform tomography at a groundwater contamination site: surface reflection data

,

Geophysics

,

2006

, vol.

72

5

(pg.

G45

-

G55

)

Gauthier

O.

,

Virieux

J.

,

Tarantola

A.

.

Two-dimensional nonlinear inversion of seismic waveforms: numerical results

,

Geophysics

,

1986

, vol.

51

7

(pg.

1387

-

1403

)

Hustedt

B.

,

Operto

S.

,

Virieux

J.

.

Mixed-grid and staggered-grid finite difference methods for frequency domain acoustic wave modelling

,

Geophys. J. Int.

,

2004

, vol.

157

(pg.

1269

-

1296

)

Jannane

M.

, et al.

Wavelengths of Earth structures that can be resolved from seismic reflection data

,

Geophysics

,

1989

, vol.

54

7

(pg.

906

-

910

)

Jin

S.

.

Inversion de données de sismique pétrolière : séparation des paramètres élastiques et détermination des vitesse de référence.

,

PhD thesis

,

1992

Université Paris 7

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Lailly

P.

.

The seismic problem as a sequence of before-stack migrations

,

Conference on Inverse Scattering: Theory and Applications

,

1983

Philadelphia

SIAM

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Lambaré

G.

,

Operto

S.

,

Podvin

P.

,

Thierry

P.

,

Noble

M.

.

3-D ray+Born migration/inversion - part 1: theory

,

Geophysics

,

2003

, vol.

68

(pg.

1348

-

1356

)

Lazaratos

S.

,

Chikichev

I.

,

Wang

K.

.

Improving the convergence rate of full wavefield inversion using spectral shaping

,

SEG Technical Program Expanded Abstracts 2011

,

2011

(pg.

2428

-

2432

)

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Martin

G.S.

,

Wiley

R.

,

Marfurt

K.J.

.

Marmousi2: An elastic upgrade for marmousi

,

Leading Edge

,

2006

, vol.

25

2

(pg.

156

-

166

)

Métivier

L.

.

Interlocked optimization and fast gradient algorithm for a seismic inverse problem

,

J. Comput. Phys.

,

2011

, vol.

230

19

(pg.

7502

-

7518

)

Métivier

L.

,

Brossier

R.

.

The seiscope optimization toolbox: a large-scale nonlinear optimization library based on reverse communication

,

Geophysics

,

2015

submitted

Google Scholar

OpenURL Placeholder Text

WorldCat

Métivier

L.

,

Lailly

P.

,

Delprat-Jannaud

F.

,

Halpern

L.

.

A 2D nonlinear inversion of well-seismic data

,

Inverse Problems

,

2011

, vol.

27

5

pg.

055005

doi:10.1088/0266-5611/27/5/055005

Métivier

L.

,

Brossier

R.

,

Virieux

J.

,

Operto

S.

.

Toward Gauss-Newton and exact Newton optimization for full waveform inversion

,

EAGE, 74th Conference and Exhibition

,

2012

Copenhagen

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Métivier

L.

,

Brossier

R.

,

Virieux

J.

,

Operto

S.

.

Full Waveform Inversion and the truncated Newton method

,

SIAM J. Sci. Comput.

,

2013

, vol.

35

2

(pg.

B401

-

B437

)

Métivier

L.

,

Bretaudeau

F.

,

Brossier

R.

,

Operto

S.

,

Virieux

J.

.

Full waveform inversion and the truncated Newton method: quantitative imaging of complex subsurface structures

,

Geophys. Prospect.

,

2014

, vol.

62

(pg.

1353

-

1375

)

Moser

T.J.

.

Review of ray-born forward modeling for migration and diffraction analysis

,

Studia Geophysica et Geodaetica

,

2012

, vol.

56

2

(pg.

411

-

432

)

Nocedal

J.

.

Updating quasi-Newton matrices with limited storage

,

Mathematics of Computation

,

1980

, vol.

35

151

(pg.

773

-

782

)

Nocedal

J.

,

Wright

S.J.

. ,

Numerical Optimization

,

2006

2nd edn

Springer

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Operto

S.

,

Ravaut

C.

,

Improta

L.

,

Virieux

J.

,

Herrero

A.

,

Dell'Aversana

P.

.

Quantitative imaging of complex structures from dense wide-aperture seismic data by multiscale traveltime and waveform inversions: a case study

,

Geophys. Prospect.

,

2004

, vol.

52

(pg.

625

-

651

)

Operto

S.

,

Virieux

J.

,

Dessa

J.X.

,

Pascal

G.

.

Crustal imaging from multi-fold ocean bottom seismometers data by frequency-domain full-waveform tomography: application to the eastern Nankai trough

,

J. geophys. Res.

,

2006

, vol.

111

pg.

B09306

doi:10.1029/2005JB003835

Operto

S.

,

Brossier

R.

,

Gholami

Y.

,

Métivier

L.

,

Prieux

V.

,

Ribodetti

A.

,

Virieux

J.

.

A guided tour of multiparameter full waveform inversion for multicomponent data: from theory to practice

,

Leading Edge

,

2013

(pg.

1040

-

1054

)

Special section Full Waveform Inversion (September)

Google Scholar

OpenURL Placeholder Text

WorldCat

Plessix

R.E.

.

A review of the adjoint-state method for computing the gradient of a functional with geophysical applications

,

Geophys. J. Int.

,

2006

, vol.

167

2

(pg.

495

-

503

)

Plessix

R.E.

.

Waveform acoustic impedance inversion with spectral shaping

,

Geophys. J. Int.

,

2013

doi:10.1093/gji/ggt233

Google Scholar

OpenURL Placeholder Text

WorldCat

Plessix

R.E.

,

Perkins

C.

.

Full waveform inversion of a deep water ocean bottom seismometer dataset

,

First Break

,

2010

, vol.

28

(pg.

71

-

78

)

Plessix

R.-E.

,

Baeten

G.

,

de Maag

J.W.

,

ten Kroode

F.

.

Full waveform inversion and distance separated simultaneous sweeping: a study with a land seismic data set

,

Geophys. Prospect.

,

2012

, vol.

60

(pg.

733

-

747

)

Podvin

P.

,

Lecomte

I.

.

Finite difference computation of traveltimes in very contrasted velocity model: a massively parallel approach and its associated tools

,

Geophys. J. Int.

,

1991

, vol.

105

(pg.

271

-

284

)

Pratt

R.G.

,

Shin

C.

,

Hicks

G.J.

.

Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion

,

Geophys. J. Int.

,

1998

, vol.

133

(pg.

341

-

362

)

Prieux

V.

,

Brossier

R.

,

Gholami

Y.

,

Operto

S.

,

Virieux

J.

,

Barkved

O.

,

Kommedal

J.

.

On the footprint of anisotropy on isotropic full waveform inversion: the Valhall case study

,

Geophys. J. Int.

,

2011

, vol.

187

(pg.

1495

-

1515

)

Prieux

V.

,

Brossier

R.

,

Operto

S.

,

Virieux

J.

.

Multiparameter full waveform inversion of multicomponent OBC data from valhall. Part 1: imaging compressional wavespeed, density and attenuation

,

Geophys. J. Int.

,

2013a

, vol.

194

3

(pg.

1640

-

1664

)

Prieux

V.

,

Brossier

R.

,

Operto

S.

,

Virieux

J.

.

Multiparameter full waveform inversion of multicomponent OBC data from valhall. Part 2: imaging compressional and shear-wave velocities

,

Geophys. J. Int.

,

2013b

, vol.

194

3

(pg.

1665

-

1681

)

Ravaut

C.

,

Operto

S.

,

Improta

L.

,

Virieux

J.

,

Herrero

A.

,

dell'Aversana

P.

.

Multi-scale imaging of complex structures from multi-fold wide-aperture seismic data by frequency-domain full-wavefield inversions: application to a thrust belt

,

Geophys. J. Int.

,

2004

, vol.

159

(pg.

1032

-

1056

)

Sevink

A.G.J.

,

Herman

G.C.

.

Three-dimensional, nonlinear, asymptotic seismic inversion

,

Inverse Problems

,

1996

, vol.

12

5

pg.

757

Shin

C.

,

Jang

S.

,

Min

D.J.

.

Improved amplitude preservation for prestack depth migration by inverse scattering theory

,

Geophys. Prospect.

,

2001

, vol.

49

(pg.

592

-

606

)

Sirgue

L.

,

Etgen

J.T.

,

Albertin

U.

.

3D frequency domain waveform inversion using time domain finite difference methods

,

Proceedings 70th EAGE, Conference and Exhibition

,

2008

Rome, Italy

pg.

F022

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Symes

W.W.

. ,

Mathematics of reflection seismology

,

1995

Rice Inversion Project

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Symes

W.W.

.

Migration velocity analysis and waveform inversion

,

Geophys. Prospect.

,

2008

, vol.

56

(pg.

765

-

790

)

Symes

W.W.

,

Carazzone

J.J.

.

Velocity inversion by differential semblance optimization

,

Geophysics

,

1991

, vol.

56

(pg.

654

-

663

)

Tarantola

A.

.

Inversion of seismic reflection data in the acoustic approximation

,

Geophysics

,

1984

, vol.

49

8

(pg.

1259

-

1266

)

ten Kroode

F.

.

A wave-equation-based kirchhoff operator

,

Inverse Problems

,

2012

, vol.

28

11

pg.

115013

doi:10.1088/0266-5611/28/11/115013

Thierry

P.

,

Lambaré

G.

,

Podvin

P.

,

Noble

M.

.

3-D preserved amplitude prestack depth migration on a workstation

,

Geophysics

,

1999a

, vol.

64

1

(pg.

222

-

229

)

Thierry

P.

,

Operto

S.

,

Lambaré

G.

.

Fast 2D ray-Born inversion/migration in complex media

,

Geophysics

,

1999b

, vol.

64

1

(pg.

162

-

181

)

Vidale

D.

.

Finite-difference calculation of travel time

,

Bull. seism. Soc. Am.

,

1988

, vol.

78

(pg.

2062

-

2076

)

Google Scholar

OpenURL Placeholder Text

WorldCat

Vigh

D.

,

Starr

B.

,

Kapoor

J.

,

Li

H.

.

3d full waveform inversion on a gulf of mexico waz data set

,

SEG Technical Program Expanded Abstracts

,

2010

, vol.

29

1

(pg.

957

-

961

)

Google Scholar

OpenURL Placeholder Text

WorldCat

Virieux

J.

,

Operto

S.

.

An overview of full waveform inversion in exploration geophysics

,

Geophysics

,

2009

, vol.

74

6

(pg.

WCC1

-

WCC26

)

Warner

M.

, et al.

Anisotropic 3D full-waveform inversion

,

Geophysics

,

2013

, vol.

78

2

(pg.

R59

-

R80

)

Zhao

H.

.

A fast sweeping method for eikonal equations

,

Mathematics of Computation

,

2005

, vol.

74

(pg.

603

-

627

)

Zhou

W.

,

Brossier

R.

,

Operto

S.

,

Virieux

J.

.

Acoustic multiparameter full-waveform inversion of diving and reflected waves through a hierarchical scheme

,

Expanded Abstracts, 84th Annual SEG Meeting

,

2014a

Denver

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Zhou

W.

,

Brossier

R.

,

Operto

S.

,

Virieux

J.

.

Combining diving and reflected waves for velocity model building by waveform inversion

,

Expanded Abstracts, 76th Annual EAGE Meeting (Amsterdam)

,

2014b

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

APPENDIX A: AMPLITUDE AND TRAVELTIME COMPUTATION FOLLOWING THE RAY THEORY

The following quantities have to be computed for the asymptotic approximation

the traveltime maps T(x; r), T(x; y);
the amplitude maps A(x; r), A(x; y).

The traveltime maps are computed through the eikonal solver of Podvin & Lecomte (1991), based on a fast-marching method. The computation of the amplitude maps depends on the geometrical spreading j(x; r), j(x; y). In 2D, considering a homogeneous medium around the source, and a proper source calibration, the amplitude satisfies

\begin{equation} A(x;r)=\frac{1}{\sqrt{-i \omega }}\sqrt{\frac{\rho (r)\rho (x)}{8\pi j(x;r)}} \end{equation}

(A1)

[see for instance Forgues (1996)]. The computation of the geometrical spreading can be performed following the paraxial ray theory. The ray coordinates q(τ), p(τ) satisfy the Ordinary Differential Equations (ODE)

\begin{equation} \left\lbrace \begin{array}{l}\displaystyle \frac{{\rm d}q}{{\rm d}\tau }=p, \\ \\ \displaystyle \frac{{\rm d}p}{{\rm d}\tau }=\frac{1}{2}\nabla \left(\frac{1}{v_{P}^2(x)}\right), \\ \\ \displaystyle \Vert p(\tau )\Vert ^2=\frac{1}{v_{P}^2(x)}. \end{array} \right. \end{equation}

(A2)

Considering a perturbation of the ray

\begin{equation} q^{\prime }(\tau )=q(\tau )+\tilde{q}(\tau ), \quad p^{\prime }(\tau )=p(\tau )+\tilde{p}(\tau ), \end{equation}

(A3)

the paraxial ODE satisfied by |$\tilde{q}(\tau ),\tilde{p}(\tau )$| is

\begin{equation} \left\lbrace \begin{array}{l}\displaystyle \frac{{\rm d}\tilde{q}}{{\rm d} \tau }=\tilde{p}, \\ \\ \displaystyle \frac{{\rm d}\tilde{p}}{{\rm d} \tau }=M\tilde{q}, \end{array} \right. \end{equation}

(A4)

where

\begin{equation} M= {\left(\begin{array}{cc}\frac{\partial ^2\,u}{\partial _{x_1^2}} &\quad \frac{\partial ^2\,u}{\partial _{x_1x_2}} \\ \frac{\partial ^2\,u}{\partial _{x_1x_2}} &\quad \frac{\partial ^2\,u}{\partial _{x_2^2}} \end{array}\right)}, \end{equation}

(A5)

and the quantity u(x) is the squared slowness

\begin{equation} u(x)=s^2(x)=\frac{1}{v_{P}^2(x)}. \end{equation}

(A6)

For the computation of the amplitude map A(x; r), point source initial conditions are chosen

\begin{equation} \left\lbrace \begin{array}{l}\tilde{q}_1=0, \quad \tilde{q}_2=0, \\ \tilde{p}_1=p_2(x;r), \quad \tilde{p}_2=-p_1(x;r). \end{array} \right. \end{equation}

(A7)

The geometrical spreading j(x; r) is given by

\begin{equation} j(x;r)=v_{P}(x)\left(p_1\tilde{q}_2-p_2\tilde{q}_1\right). \end{equation}

(A8)

The workflow for computing j(x; r) is thus as follows:

Compute the traveltimes from the receiver r using the eikonal solver.
Perform a back ray tracing from the point x to the receiver r using the gradient of the traveltime ∇T(x; r).
Store the components p₁ and p₂ at x and at the receiver r.
Get the initial condition for the paraxial ray tracing and solve the paraxial equations (A4).
Compute j(x; r) following formula (A8).

APPENDIX B: COMPUTATION OF THE BEYLKIN INTEGRAL OPERATOR |$\scr {B}$| AND ITS ADJOINT |$\scr {B}^{*}$|

The integral operator |$\scr {B}$| is defined through its kernel, which depends on the function h(x_r, x_s, ω) defined in eq. (38). For the sake of simplicity, the explicit formulation of |$\scr {B}$| is given for the 2D mono-parameter case (constant density is assumed).

The computation of h(x_r, x_s, ω) requires to develop the expression of the Jacobian associated with the change of variable f defined in eq. (32). This Jacobian has been denoted by (Df)(|k|, Ψ, θ). The definition of k in eq. (31) implies

\begin{equation} |k|=\omega \sqrt{\left\Vert \nabla T(x,x_{\rm r})+\nabla T(x,x_{\rm s})\right\Vert ^2} =\omega \sqrt{\left\Vert \nabla T(x,x_{\rm r})\right\Vert ^2+\left\Vert \nabla T(x,x_{\rm r})\right\Vert ^2+2\nabla T(x,x_{\rm r})\cdot\nabla T(x,x_{\rm s})}. \end{equation}

(B1)

The definition of the phase vectors T(x, x_r) and T(x, x_s) yields

\begin{equation} \left\Vert \nabla T(x,x_{\rm r})\right\Vert ^2=\left\Vert \nabla T(x,x_{\rm s})\right\Vert ^2=\frac{1}{v_{P}^2(x)}. \end{equation}

(B2)

In addition,

\begin{equation} \nabla T(x,x_{\rm r}).\nabla T(x,x_{\rm s})=\frac{\cos \theta (x_{\rm r},x,x_{\rm s})}{v_{P}^2(x)}. \end{equation}

(B3)

The trigonometric identity

\begin{equation} \cos x = 2 \cos ^2 \left(x/2\right)-1 \end{equation}

(B4)

yields

\begin{equation} |k|=\omega \frac{2|\cos \left(\frac{\theta }{2}\right)|}{v_{P}(x)}. \end{equation}

(B5)

This implies that

\begin{equation} \frac{\partial \omega }{\partial |k|}=\frac{v_{P}(x)}{2|\cos \left(\frac{\theta }{2}\right)|}. \end{equation}

(B6)

Therefore, (Df)(|k|, Ψ, θ) can be simplified into

\begin{equation} (Df)(|k|,\Psi ,\theta )= {\left(\begin{array}{ccc}\frac{v_{P}(x)}{2|\cos \left(\frac{\theta }{2}\right)|}&\quad 0&\quad 0 \\ 0&\quad \frac{\partial x_{\rm r}}{\partial \Psi }&\quad \frac{x_{\rm r}}{\partial \theta } \\ 0&\quad \frac{\partial x_{\rm s}}{\partial \Psi }&\quad \frac{x_{\rm s}}{\partial \theta } \end{array}\right)} \end{equation}

(B7)

and

\begin{equation} \det (Df)(|k|,\Psi ,\theta )= \frac{v_{P}(x)}{2|\cos \left(\frac{\theta }{2}\right)|} \left( \frac{\partial x_{\rm r}}{\partial \Psi }\frac{x_{\rm s}}{\partial \theta } -\frac{\partial x_{\rm s}}{\partial \Psi }\frac{x_{\rm r}}{\partial \theta } \right). \end{equation}

(B8)

The definition of the angles Ψ and θ (eq. 33) implies that

\begin{equation} \frac{\partial x_{\rm r}}{\partial \Psi }=\frac{2\partial x_{\rm r}}{\partial \phi _{\rm r}}, \quad \frac{\partial x_{\rm s}}{\partial \Psi }=\frac{2\partial x_{\rm s}}{\partial \phi _{\rm s}}, \quad \frac{x_{\rm r}}{\partial \theta } =\frac{\partial x_{\rm r}}{\partial \phi _{\rm r}}, \quad \frac{x_{\rm s}}{\partial \theta } =-\frac{\partial x_{\rm s}}{\partial \phi _{\rm s}}. \end{equation}

(B9)

Therefore

\begin{equation} \det (Df)(|k|,\Psi ,\theta )= \frac{-4v_{P}(x)}{|\cos \left(\frac{\theta }{2}\right)|} \frac{\partial x_{\rm r}}{\partial \phi _{\rm r}}\frac{\partial x_{\rm s}}{\partial \phi _{\rm s}}. \end{equation}

(B10)

The quantities |$\frac{\partial x_{\rm s}}{\partial \phi _{\rm s}}$| and |$\frac{\partial x_{\rm r}}{\partial \phi _{\rm r}}$| can be expressed using the geometrical spreading function j(y, x),

\begin{equation} \frac{\partial x_{\rm s}}{\partial \phi _{\rm s}}=\frac{j(x_{\rm s},x)}{\cos \varphi _{\rm s}}, \quad \frac{\partial x_{\rm r}}{\partial \phi _{\rm r}}=\frac{j(x_{\rm r},x)}{\cos \varphi _{\rm r}}, \end{equation}

(B11)

where the angles φ_r and φ_s are the angles made with the vertical by the tangent to the ray connecting x to x_r and x_s, respectively (see Fig. 1). The geometrical spreading function is useful for computing the amplitude terms A(y, x). They can be efficiently estimated using the paraxial ray theory (Appendix A). The determinant |$\det (Df)(|k|,\Psi ,\theta )$| can thus be expressed as

\begin{equation} \det (Df)(|k|,\Psi ,\theta )= \frac{-4v_{P}(x)}{|\cos \left(\frac{\theta }{2}\right)|} \frac{j(x_{\rm s},x)}{\cos \varphi _{\rm s}}\frac{j(x_{\rm r},x)}{\cos \varphi _{\rm r}}. \end{equation}

(B12)

In the mono-parameter context (constant density), the matrices W(θ) and M₀(x) are scalar quantities such that

\begin{equation} W(\theta )=1, \quad M_0(x)^{-1}=\frac{1}{\rho (x)v_{P}^2(x)} \end{equation}

(B13)

Equations (B12), (B5) and (38) thus yield

\begin{equation} h(x,x_{\rm r},x_{\rm s},\omega )= \frac{\omega \cos ^2\left(\frac{\theta }{2}\right) |\cos \varphi _{\rm s}| |\cos \varphi _{\rm r}|}{2\rho (x)v_{P}^4(x)j(x_{\rm s},x)j(x_{\rm r},x)\left(\theta _{{\rm max}}(x)-\theta _{{\rm min}}(x)\right)}. \end{equation}

(B14)

Using again the trigonometric identity (B4) and geometrical spreading function reciprocity equation

\begin{equation} j(x,y)=j(y,x)\frac{v_{P}(x)}{v_{P}(y)}, \end{equation}

(B15)

the weighting function h(x, x_r, x_s, ω) can be written as

\begin{equation} h(x,x_{\rm r},x_{\rm s},\omega )=\frac{\omega \left(\cos \theta +1\right) |\cos \varphi _{\rm s}| |\cos \varphi _{\rm r}|}{4\rho (x)v_{P}^2(x)v_{P}(x_{\rm s})v_{P}(x_{\rm r})j(x,x_{\rm s})j(x,x_{\rm r})\left(\theta _{{\rm max}}(x)-\theta _{{\rm min}}(x)\right)}. \end{equation}

(B16)

Therefore, for all |$d\in \scr {D}$|⁠,

\begin{equation} \begin{array} {ll} \displaystyle \left(\scr {B}d\right)(x)= \int _{\partial \Omega _{\rm r}}\int _{\partial \Omega _{\rm s}}\int _{0}^{\infty } & \displaystyle \frac{\left(\cos \theta +1\right) |\cos \varphi _{\rm s}| |\cos \varphi _{\rm r}|}{4\omega A(x_{\rm r},x,x_{\rm s})v_{P}(x_{\rm s})v_{P}(x_{\rm r})j(x,x_{\rm s})j(x,x_{\rm r})\left(\theta _{{\rm max}}-\theta _{{\rm min}}\right)} e^{-i\omega T(x_{\rm r},x,x_{\rm s})} \\ \\ \displaystyle &{\rm d}(x_{\rm r},x_{\rm s},\omega ) {\rm d}x_{\rm r} \;{\rm d}x_{\rm s} \;{\rm d}\omega {.} \end{array} \end{equation}

(B17)

From (B17), the computation of the adjoint |$\scr {B}^{*}$| is straightforward. For all |$m \in \scr {M}$|⁠, we have

\begin{equation} \begin{array}{ll} \displaystyle \left(\scr {B}^{*}m\right)(x_{\rm r},x_{\rm s},\omega )= \int _{\Omega } & \displaystyle \frac{\left(\cos \theta +1\right) |\cos \varphi _{\rm s}| |\cos \varphi _{\rm r}|}{4\omega A(x_{\rm r},x,x_{\rm s})v_{P}(x_{\rm s})v_{P}(x_{\rm r})j(x,x_{\rm s})j(x,x_{\rm r})\left(\theta _{{\rm max}}-\theta _{{\rm min}}\right)} e^{i\omega T(x_{\rm r},x,x_{\rm s})} m(x){\rm d}x. \end{array} \end{equation}

(B18)

Download all slides

Month:	Total Views:
January 2017	3
February 2017	4
March 2017	3
April 2017	4
May 2017	2
June 2017	8
August 2017	6
October 2017	2
November 2017	1
December 2017	2
January 2018	2
February 2018	14
April 2018	3
May 2018	1
June 2018	12
July 2018	19
August 2018	20
September 2018	9
October 2018	18
November 2018	7
December 2018	9
January 2019	12
February 2019	16
March 2019	20
April 2019	14
May 2019	8
June 2019	6
July 2019	24
August 2019	13
September 2019	23
October 2019	9
November 2019	19
December 2019	10
January 2020	17
February 2020	10
March 2020	6
April 2020	14
May 2020	7
June 2020	8
July 2020	23
August 2020	9
September 2020	2
November 2020	15
December 2020	6
January 2021	8
February 2021	7
March 2021	15
April 2021	8
May 2021	7
June 2021	3
July 2021	21
August 2021	4
September 2021	5
October 2021	8
November 2021	14
December 2021	6
January 2022	19
February 2022	11
March 2022	13
April 2022	20
May 2022	5
June 2022	4
July 2022	12
August 2022	24
September 2022	23
October 2022	21
November 2022	8
December 2022	4
January 2023	11
February 2023	2
March 2023	5
April 2023	4
May 2023	8
June 2023	2
July 2023	6
August 2023	6
September 2023	8
October 2023	9
November 2023	7
December 2023	14
January 2024	2
February 2024	9
March 2024	4
April 2024	7

Article Contents

Combining asymptotic linearized inversion and full waveform inversion

Abstract

1 INTRODUCTION

2 LINEARIZED SEISMIC INVERSE PROBLEM

2.1 Definitions and notations

2.2 Linearized inversion

2.3 First-order Born approximation

2.4 Asymptotic approximation: computation of |$\scr {J}(m_0)$|

2.5 Computation of |$\scr {B}(m_0)$|

3 MODIFICATION OF THE STANDARD FWI MISFIT FUNCTION

3.1 The FWI problem

3.2 Link with the linearized inverse problem

3.3 Introducing the asymptotic inverse within the FWI process

4 NUMERICAL STUDY

4.1 Experimental settings and implementation

4.2 A canonical test case: reconstruction of two inclusions in a smooth background model

4.3 Application to the Marmousi model

4.4 Application to the synthetic Valhall model

5 DISCUSSION

6 CONCLUSION

REFERENCES

APPENDIX A: AMPLITUDE AND TRAVELTIME COMPUTATION FOLLOWING THE RAY THEORY

APPENDIX B: COMPUTATION OF THE BEYLKIN INTEGRAL OPERATOR |$\scr {B}$| AND ITS ADJOINT |$\scr {B}^{*}$|

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Combining asymptotic linearized inversion and full waveform inversion

Abstract

1 INTRODUCTION

2 LINEARIZED SEISMIC INVERSE PROBLEM

2.1 Definitions and notations

2.2 Linearized inversion

2.3 First-order Born approximation

2.4 Asymptotic approximation: computation of |$\scr {J}(m_0)$|

2.5 Computation of |$\scr {B}(m_0)$|

3 MODIFICATION OF THE STANDARD FWI MISFIT FUNCTION

3.1 The FWI problem

3.2 Link with the linearized inverse problem

3.3 Introducing the asymptotic inverse within the FWI process

4 NUMERICAL STUDY

4.1 Experimental settings and implementation

4.2 A canonical test case: reconstruction of two inclusions in a smooth background model

4.3 Application to the Marmousi model

4.4 Application to the synthetic Valhall model

5 DISCUSSION

6 CONCLUSION

REFERENCES

APPENDIX A: AMPLITUDE AND TRAVELTIME COMPUTATION FOLLOWING THE RAY THEORY

APPENDIX B: COMPUTATION OF THE BEYLKIN INTEGRAL OPERATOR |$\scr {B}$| AND ITS ADJOINT |$\scr {B}^{*}$|

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only