Abstract
Inner core translation, with solidification on one hemisphere and melting on the other, provides a promising basis for understanding the hemispherical dichotomy of the inner core, as well as the anomalous stable layer observed at the base of the outer core—the so-called F-layer—which might be sustained by continuous melting of inner core material. In this paper, we study in details the dynamics of inner core thermal convection when dynamically induced melting and freezing of the inner core boundary (ICB) are taken into account.
If the inner core is unstably stratified, linear stability analysis and numerical simulations consistently show that the translation mode dominates only if the viscosity η is large enough, with a critical viscosity value, of order ∼3 × 1018 Pa s, depending on the ability of outer core convection to supply or remove the latent heat of melting or solidification. If η is smaller, the dynamic effect of melting and freezing is small. Convection takes a more classical form, with a one-cell axisymmetric mode at the onset and chaotic plume convection at large Rayleigh number. η being poorly known, either mode seems equally possible. We derive analytical expressions for the rates of translation and melting for the translation mode, and a scaling theory for high Rayleigh number plume convection. Coupling our dynamic models with a model of inner core thermal evolution, we predict the convection mode and melting rate as functions of inner core age, thermal conductivity, and viscosity. If the inner core is indeed in the translation regime, the predicted melting rate is high enough, according to Alboussière et al.'s experiments, to allow the formation of a stratified layer above the ICB. In the plume convection regime, the melting rate, although smaller than in the translation regime, can still be significant if η is not too small.
Thermal convection requires that a superadiabatic temperature profile is maintained in the inner core, which depends on a competition between extraction of the inner core internal heat by conduction and cooling at the ICB. Inner core thermal convection appears very likely with the low thermal conductivity value proposed by Stacey & Loper, but nearly impossible with the much higher thermal conductivity recently put forward by Sha & Cohen, de Koker et al. and Pozzo et al. We argue however that the formation of an iron-rich layer above the ICB may have a positive feedback on inner core convection: it implies that the inner core crystallized from an increasingly iron-rich liquid, resulting in an unstable compositional stratification which could drive inner core convection, perhaps even if the inner core is subadiabatic.
1 INTRODUCTION
In the classical model of convection and dynamo action in Earth's outer core, convection is thought to be driven by a combination of cooling from the core–mantle boundary (CMB) and light elements (O, Si, S, …) and latent heat release at the inner core boundary (ICB). Convection is expected to be vigorous, and the core must therefore be very close to adiabatic, with only minute lateral temperature variations (Stevenson 1987), except in very thin, unstable boundary layers at the ICB and CMB. To a large extent, seismological models are consistent with the bulk of the core being well-mixed and adiabatic, which supports the standard model of outer core convection. Yet seismological observations indicate the existence of significant deviations from adiabaticity in the lowermost ∼200 km of the outer core (Souriau & Poupinet 1991). This layer, sometimes called F-layer for historical reasons, exhibits an anomalously low VP gradient which is most probably indicative of stable compositional stratification (Gubbins et al.2008), implying that the lowermost 200 km of the outer core are depleted in light elements compared to the bulk of the core. This is in stark contrast with the classical model of outer core convection sketched above: in place of the expected thin unstable boundary layer, seismological models argues for a very thick and stable layer. Note also that the thickness of the layer, ∼200 km, is much larger than any diffusion length scales, even on a Gy timescale, which means that if real this layer must have been created, and be sustained, by a mechanism involving advective transport.
Because light elements are partitioned preferentially into the liquid during solidification, iron-rich melt can be produced through a two-stage purification process involving solidification followed by melting (Gubbins et al.2008). Based on this idea, Gubbins et al. (2008) have proposed a model for the formation of the F-layer in which iron-rich crystals nucleate at the top of the layer and melt back as they sink towards the ICB, thus implying a net inward transport of iron which results in a stable stratification. In contrast, Alboussière et al. (2010) proposed that melting occurs directly at the ICB in response to inner core internal dynamics, in spite of the fact that the inner core must be crystallizing on average. Assuming that the inner core is melting in some regions while it is crystallizing in others, the conceptual model proposed by Alboussière et al. (2010) works as follow: melting inner core material produces a dense iron-rich liquid which spreads at the surface of the inner core, while crystallization produces a buoyant liquid which mixes with and carries along part of the dense melt as it rises. The stratified layer results from a dynamic equilibrium between production of iron-rich melt and entrainment and mixing associated with the release of buoyant liquid. Analogue fluid dynamics experiments demonstrate the viability of the mechanism, and show that a stratified layer indeed develops if the buoyancy flux associated with the dense melt is larger (in magnitude) than a critical fraction (≃80 per cent) of the buoyancy flux associated with the light liquid. This number is not definitive because possibly important factors were absent in Alboussière et al. (2010)'s experiments (Coriolis and Lorentz force, entrainment by thermal convection from above, …) but it seems likely that a high rate of melt production will still be required.
A plausible way to melt the inner core is to sustain dynamically a topography that will bring locally the ICB at a potential temperature lower than that of the adjacent liquid core, which allows heat to flow from the outer core to the inner core. The melting rate is then limited by the ability of outer core convection to provide the latent heat absorbed by melting, and only a significant ICB topography can lead to a non-negligible melting rate. More recently, Gubbins et al. (2011) and Sreenivasan & Gubbins (2011) have proposed that localized melting of the inner core might be induced by outer core convection, but the predicted rate of melt production is too small to produce a stratified layer according to Alboussière et al. (2010)'s experiments. Furthermore, it is not clear that the behaviour observed in numerical simulations at slightly supercritical conditions would persist at Earth's core conditions.
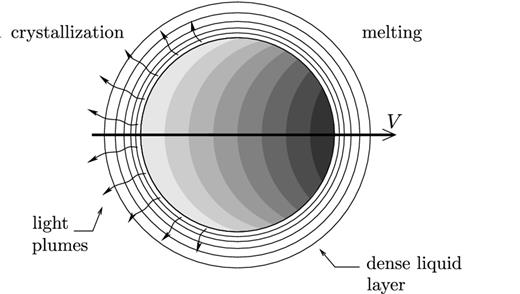
Among the different models of inner core dynamics proposed so far (Jeanloz & Wenk 1988; Yoshida et al.1996; Karato 1999; Buffett & Wenk 2001; Deguen et al.2011), only thermal convection (Jeanloz & Wenk 1988; Weber & Machetel 1992; Buffett 2009; Deguen & Cardin 2011; Cottaar & Buffett 2012) is potentially able to produce a large dynamic topography and associated melting. Thermal convection in the inner core is possible if the growth rate of the inner core is large enough and its thermal conductivity low enough (Sumita et al.1995; Buffett 2009; Deguen & Cardin 2011). One possible mode of inner core thermal convection consists in a global translation with solidification on one hemisphere and melting on the other (Monnereau et al.2010; Alboussière et al.2010; Mizzon & Monnereau 2013). The translation rate can be such that the rate of melt production is high enough to explain the formation of the F-layer (Alboussière et al.2010). In addition, inner core translation provides a promising basis for understanding the hemispherical dichotomy of the inner core observed in its seismological properties (Tanaka & Hamaguchi 1997; Niu & Wen 2001; Irving et al.2009; Tanaka 2012). Textural change of the iron aggregate during the translation (Bergman et al.2010; Monnereau et al.2010; Geballe et al.2013) may explain the hemispherical structure of the inner core. Inner core translation, by imposing a highly asymmetric buoyancy flux at the base of the outer core, is also a promising candidate (Aubert 2013; Davies et al.2013) for explaining the existence of the planetary scale eccentric gyre which has been inferred from quasi-geostrophic core flow inversions (Pais et al.2008; Gillet et al.2009).
However, inner core translation induces horizontal temperature gradients (see Fig. 1), and Alboussière et al. (2010) noted that finite deformation associated with these density gradients is expected to weaken the translation mode if the inner core viscosity is too small. They estimated from an order of magnitude analysis that the threshold would be at η ∼ 1018 Pa s. Below this threshold, thermal convection is expected to take a more classical form, with cold plumes falling down from the ICB and warmer upwellings (Deguen & Cardin 2011). Published estimates of inner core viscosity range from ∼1011 to ∼1022 Pa s (Yoshida et al.1996; Buffett 1997; Van Orman 2004; Koot & Dumberry 2011; Reaman et al.2011, 2012) implying that both convection regime seem possible.
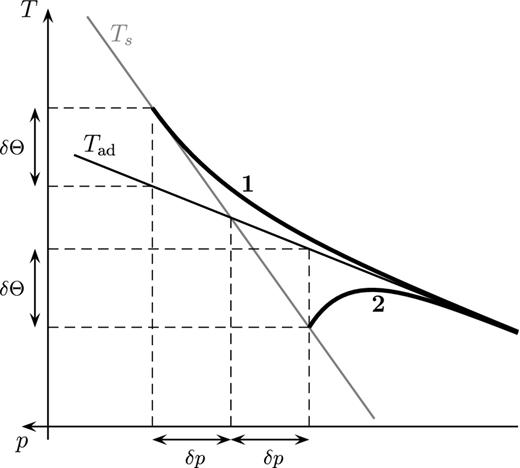
A schematic representation of the translation mode of the inner core, with the grey shading showing the potential temperature distribution (or equivalently the density perturbation) in a cross-section including the translation direction (adapted from Alboussière et al.2010).
The purpose of this paper is twofold: (i) to precise under what conditions the translation mode can be active, and (ii) to estimate the rate of melt production associated with convection, in particular when the effect of finite viscosity becomes important. To this aim, we develop a set of equations for thermal convection in the inner core with phase change associated with a dynamically sustained topography at the inner core boundary (Section 3). The kinetics of phase change is described by a non-dimensional number, noted |$\mathcal {P}$| for ‘phase change number’, which is the ratio of a phase change timescale (introduced in Section 2) to a viscous relaxation timescale. The linear stability analysis of the set of equations (Section 4) demonstrates that the first unstable mode of thermal convection consists in a global translation when |$\mathcal {P}$| is small. When |$\mathcal {P}$| is large, the first unstable mode is the classical one cell convective mode of thermal convection in a sphere with an impermeable boundary (Chandrasekhar 1961). An analytical expression for the rate of translation is derived in Section 5. We then describe numerical simulation of thermal convection, from which we derive scaling laws for the rate of melt production (Section 6). The results of the previous sections are then applied to the inner core, and used to predict the convection regime of the inner core and the rate of melt production as functions of the inner core growth rate and thermophysical parameters (Section 7).
2 PHASE CHANGE AT THE ICB
Temperature profiles (thick black lines) in the vicinity of the inner core boundary. Profile 1 corresponds to a crystallizing region, while profile 2 corresponds to a melting region. The thin black line is the outer core adiabat Tad and the thin grey line is the solidification temperature profile.
Thermophysical parameters used in this study.
| Parameter | Symbol | Value |
|---|---|---|
| Inner core radiusa | ricb | 1221 km |
| Solidification temperatureb | Ticb | 5600 ± 500 K |
| Gruneisen parameterc | γ | 1.4 ± 0.1 |
| Thermal expansionc | α | (1.1 ± 0.1) × 10−5 K−1 |
| Heat capacityd | cp | 800 ± 80 J kg−1 K−1 |
| Latent heat of meltingd, e | L | 600–1200 kJ kg−1 |
| Density jump at the ICBa | Δρ | 600 kg m−3 |
| Density in the inner corea | ρs | 12 800 kg m−3 |
| Density in the outer core at the ICBa | ρl | 12 200 kg m−3 |
| Gravity at the ICBa | gicb | 4.4 m s−2 |
| Radial gravity gradienta | g′ | 3.6 × 10−6 s−2 |
| Thermal conductivityf | k | 36–150 W m−1 K−1 |
| Isentropic bulk modulusa | KS | 1400 GPa |
| Clapeyron/adiabat slopes ratiog | dTs/dTad | 1.65 ± 0.11 |
| Parameter | Symbol | Value |
|---|---|---|
| Inner core radiusa | ricb | 1221 km |
| Solidification temperatureb | Ticb | 5600 ± 500 K |
| Gruneisen parameterc | γ | 1.4 ± 0.1 |
| Thermal expansionc | α | (1.1 ± 0.1) × 10−5 K−1 |
| Heat capacityd | cp | 800 ± 80 J kg−1 K−1 |
| Latent heat of meltingd, e | L | 600–1200 kJ kg−1 |
| Density jump at the ICBa | Δρ | 600 kg m−3 |
| Density in the inner corea | ρs | 12 800 kg m−3 |
| Density in the outer core at the ICBa | ρl | 12 200 kg m−3 |
| Gravity at the ICBa | gicb | 4.4 m s−2 |
| Radial gravity gradienta | g′ | 3.6 × 10−6 s−2 |
| Thermal conductivityf | k | 36–150 W m−1 K−1 |
| Isentropic bulk modulusa | KS | 1400 GPa |
| Clapeyron/adiabat slopes ratiog | dTs/dTad | 1.65 ± 0.11 |
Thermophysical parameters used in this study.
| Parameter | Symbol | Value |
|---|---|---|
| Inner core radiusa | ricb | 1221 km |
| Solidification temperatureb | Ticb | 5600 ± 500 K |
| Gruneisen parameterc | γ | 1.4 ± 0.1 |
| Thermal expansionc | α | (1.1 ± 0.1) × 10−5 K−1 |
| Heat capacityd | cp | 800 ± 80 J kg−1 K−1 |
| Latent heat of meltingd, e | L | 600–1200 kJ kg−1 |
| Density jump at the ICBa | Δρ | 600 kg m−3 |
| Density in the inner corea | ρs | 12 800 kg m−3 |
| Density in the outer core at the ICBa | ρl | 12 200 kg m−3 |
| Gravity at the ICBa | gicb | 4.4 m s−2 |
| Radial gravity gradienta | g′ | 3.6 × 10−6 s−2 |
| Thermal conductivityf | k | 36–150 W m−1 K−1 |
| Isentropic bulk modulusa | KS | 1400 GPa |
| Clapeyron/adiabat slopes ratiog | dTs/dTad | 1.65 ± 0.11 |
| Parameter | Symbol | Value |
|---|---|---|
| Inner core radiusa | ricb | 1221 km |
| Solidification temperatureb | Ticb | 5600 ± 500 K |
| Gruneisen parameterc | γ | 1.4 ± 0.1 |
| Thermal expansionc | α | (1.1 ± 0.1) × 10−5 K−1 |
| Heat capacityd | cp | 800 ± 80 J kg−1 K−1 |
| Latent heat of meltingd, e | L | 600–1200 kJ kg−1 |
| Density jump at the ICBa | Δρ | 600 kg m−3 |
| Density in the inner corea | ρs | 12 800 kg m−3 |
| Density in the outer core at the ICBa | ρl | 12 200 kg m−3 |
| Gravity at the ICBa | gicb | 4.4 m s−2 |
| Radial gravity gradienta | g′ | 3.6 × 10−6 s−2 |
| Thermal conductivityf | k | 36–150 W m−1 K−1 |
| Isentropic bulk modulusa | KS | 1400 GPa |
| Clapeyron/adiabat slopes ratiog | dTs/dTad | 1.65 ± 0.11 |
3 GOVERNING EQUATIONS
3.1 Equations within the inner core
Since Di/γ ≃ 0.05, the vorticity source arising from self-gravitation effects might be up to ∼15 per cent of the total vorticity production if the length scale of convection is similar to the inner core radius, but has a much smaller contribution when λ/ric is small. Although the approximation might not be very good in cases where λ is comparable to ric, we will ignore here the radial variations of |$\bar{\rho }$|, without which the force arising from self-gravitation is potential, and is therefore balanced by the pressure field. The density in the inner core is assumed to be uniform: |$\overline{\rho } = \rho _s$|. To be consistent, |$\overline{g}$| is assumed to be a linear function of radius, |$\overline{g}=g_\mathrm{icb} r/r_\mathrm{ic}$|. Density in the liquid outer core is assumed to be uniform as well: |$\overline{\rho _l} = \rho _l$|. This is not correct for the outer core as a whole, but this is an excellent approximation within the depth range of the expected topography of the inner core boundary, so that ρl is the density of the outer core close to the inner core for our purpose.
3.2 Expression of boundary conditions
Finally, the radial velocity ur at the ICB is related to the topography h and gravitational potential perturbation Ψ′ through the heat balance at the ICB (eq. 7).
3.3 Set of equations
4 LINEAR STABILITY ANALYSIS
We investigate here the linear stability of the system of equations describing thermal convection in the inner core with phase change at the ICB, as derived in Section 3. The calculation given here is a generalization of the linear stability analysis of thermal convection in an internally heated sphere given by Chandrasekhar (1961). The case considered by Chandrasekhar (1961), where a non-deformable, impermeable outer boundary is assumed, corresponds to the limit |$\mathcal {P}\rightarrow \infty$| of the problem considered here.
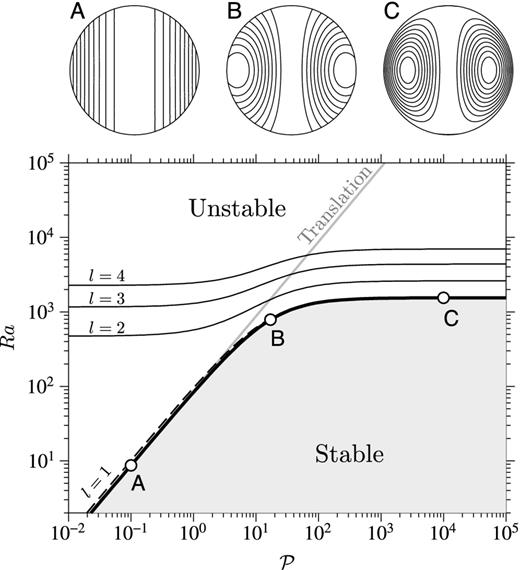
Stability diagram for convection in a sphere with phase change at its outer boundary. The neutral stability curve (l = 1) obtained by solving eq. (84) with σ1 = 0 is shown by the thick black line. The dashed line shows the approximate stability curve given by eq. (86). The neutral stability curves of higher modes (l = 2, 3, 4) obtained by solving eq. (83) with σl = 0 are shown by the annotated thin black lines. The neutral stability curves for l ≥ 5 are not shown to avoid overcrowding the figure. The thick grey curve annotated ‘Translation’ is the neutral stability curve of the translation mode, given by eq. (94). Streamlines of the first unstable mode at points A (|$\mathcal {P} = 0.1$|), B (|$\mathcal {P} = 17$|) and C (|$\mathcal {P} = 10^4$|) are shown in the upper figure.
At high |$\mathcal {P}$|, the term in |$1/\mathcal {P}$| in eq. (90) becomes negligible, and the first unstable mode is identical to the classical single cell degree one mode of thermal convection with shear-free boundary and no phase change (Chandrasekhar 1961), as illustrated in Fig. 3 (point C, |$\mathcal {P}=10^4$|). There is no melting or solidification associated with this mode, which is apparent from the fact that the streamlines of the flow are closed. At intermediate values of |$\mathcal {P}$|, the first unstable mode is a linear combination of the high-|$\mathcal {P}$| convection mode and of the small-|$\mathcal {P}$| translation mode.
Finally, it can be seen in Fig. 3 that the critical Rayleigh number |$Ra_c^l$| for higher order modes (l > 1) is also lowered when |$\mathcal {P}\lesssim 17$|. However, the decrease in |$Ra_c^l$| is not as drastic as it is for the l = 1 mode because, whatever the value of |$\mathcal {P}$|, viscous dissipation always limits the growth of these modes. The effect of |$\mathcal {P}$| on |$Ra_c^l$| becomes increasingly small as l increases. This suggests that allowing for phase change at the ICB would generally enhance large scale motions at the expense of smaller scale motions.
5 ANALYTICAL SOLUTIONS FOR SMALL |$\mathcal {P}$|
We now search for a finite amplitude solution of inner core convection at small |$\mathcal {P}$|. In the limit of infinite viscosity (|$\mathcal {P}\rightarrow 0$|), the only possible motions of the inner core are rotation, which we do not consider here, and translation. Guided by the results of the linear stability analysis, we search for a solution in the form of a translation. Alboussière et al. (2010) found a solution for the velocity of inner core translation from a global force balance on the inner core, under the assumption that the inner core is rigid. One of the goal of this section is to verify that the system of equations developed in Section 3 indeed leads to the same solution when |$\mathcal {P}\rightarrow 0$|.
If the viscosity is taken as infinite and |$\mathcal {P}$| is formally put to zero, searching for a pure translation solution and ignoring any deformation in the inner core leads to an undetermined system. Translation is an exact solution of the momentum equation, but the translation rate is left undetermined, because all the terms in the boundary conditions (55), (56) and (57) (zero tangential stress and continuity of the normal stress) vanish. This of course does not mean that the stress magnitude vanishes, but rather that the rheological relationship between stress and strain via the viscosity becomes meaningless if the viscosity is assumed to be infinite. The ICB topography associated with the translation is sustained by the non-hydrostatic stress field which, even if η → ∞, must remain finite. One way to calculate the stress field is to evaluate the flow induced by the lateral temperature variations associated with the translation, for small but non-zero |$\mathcal {P}$|, and then take the limit |$\mathcal {P}\rightarrow 0$|. If only the ‘rigid inner core’ limit is wanted, it suffices to calculate the flow at |$\mathcal {O}(\mathcal {P})$|. The effect of finite viscosity on the translation mode can be estimated by calculating the velocity field at a higher order in |$\mathcal {P}$|.
5.1 Translation velocity at zeroth order in |$\mathcal {P}$|
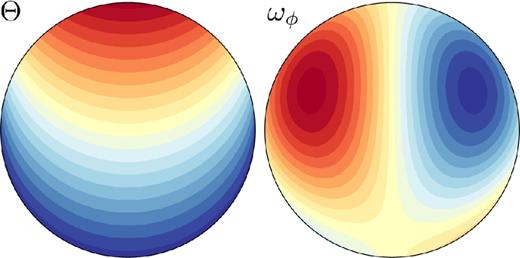
Temperature field (left, red = hot, blue = cold) and vorticity field at |$\mathcal {O}(\cal {P})$| (right, blue = negative, red = positive) in a meridional cross-section (the direction of translation is arbitrary).
5.2 Translation velocity at |$\mathcal {O}(\mathcal {P})$|
The temperature field and the ϕ-component of the vorticity field at |$\mathcal {O}(\mathcal {P})$|, as calculated in Appendix B, are shown in figure (4).
5.3 The effect of the boundary layer
5.4 Melt production
6 NUMERICAL RESULTS AND SCALING LAWS
6.1 Method
The code is an extension of the one used in Deguen & Cardin (2011), with the boundary condition derived in Section 3 now implemented. The system of equations derived in Section 3 is solved in 3-D, using a spherical harmonic expansion for the horizontal dependence and a finite difference scheme in the radial direction. The radial grid can be refined below the ICB if needed. The non-linear part of the advection term in the temperature equation is evaluated in the physical space at each time step. A semi-implicit Crank- Nickolson scheme is implemented for the time evolution of the linear terms and an Adams–Bashforth procedure is used for the non-linear advection term in the heat equation. The temperature field is initialized with a random noise covering the full spectrum. We use up to 256 radial points and 128 spherical harmonics degree. Care has been taken that the ICB thermal boundary layer, which can be very thin in the translation mode, is always well resolved.
The code has the ability to take into account the growth of the inner core and the evolution of the internal heating rate S(t), which is calculated from the thermal evolution of the outer core (Deguen & Cardin 2011). In this section, we will first focus on simulations with a constant inner core radius and steady thermal forcing (internal heating rate S constant). Simulations with an evolving inner core will be presented in Section 7.
Each numerical simulation was run for at least 10 overturn times ric/Urms, where Urms is the rms velocity in the inner core.
6.2 Overview
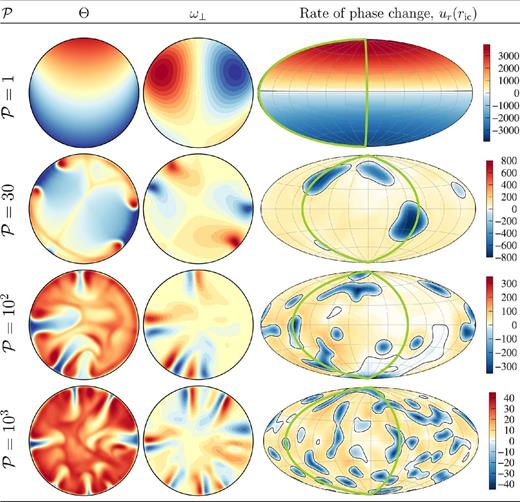
As already suggested by the linear stability analysis (Section 4) and the small |$\mathcal {P}$| analytical model (Section 5), the translation mode is expected to be dominant when |$\mathcal {P}$| is small. This is confirmed by our numerical simulations. As an example, Fig. 5 shows outputs of simulations with the same Rayleigh number value of Ra = 107 and |$\mathcal {P}=1$|, 30, 102 and 103. Snapshots of cross-sections of the potential temperature field and vorticity (its component perpendicular to the cross-section plane) are shown in the first and second columns, and maps of radial velocity ur(ric) at the ICB are shown in the third column. ur(ric) is equal to the local phase change rate, with positive values corresponding to melting and negative values corresponding to solidification.
Snapshots from numerical simulations with Ra = 107 and |$\mathcal {P}=1$|, 30, 100 and 103, showing potential temperature Θ (first column), azimuthal vorticity ω⊥ (second column) and radial velocity ur(ric) at the outer boundary (third column).
At the lowest |$\mathcal {P}$| (|$\mathcal {P}=1$|), the translation mode is clearly dominant, with the pattern of temperature and vorticity similar to the predictions of the analytical models of Section 5 shown in Fig. 4. In contrast, the convection regime at the largest |$\mathcal {P}$| (|$\mathcal {P}=10^3$|) appears to be qualitatively similar to the regime observed with impermeable boundary conditions (Weber & Machetel 1992; Deguen & Cardin 2011), which corresponds to the limit |$\mathcal {P}\rightarrow \infty$|. At the Rayleigh number considered here, convection is chaotic and takes the form of cold plumes originating from a thin thermal boundary layer below the ICB, with a passive upward return flow. At intermediate values of |$\mathcal {P}$| (|$\mathcal {P}=30$| and 102), phase change has still a significant effect on the pattern of the flow, with large scale components of the flow enhanced by phase change at the ICB, in qualitative agreement with the prediction of the linear stability analysis. Note that at |$\mathcal {P}=10^2$|, there is still a clear hemispherical pattern, with plumes originating preferentially from one hemisphere.
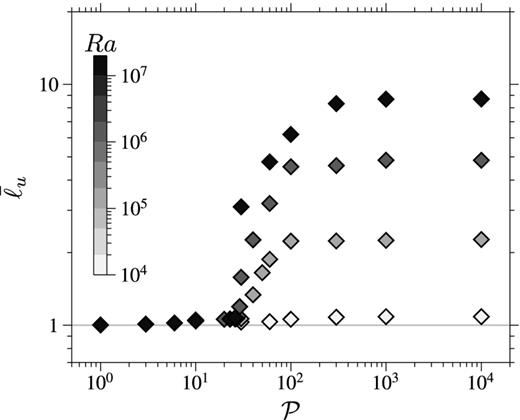
Fig. 6 shows the calculated value of |${\skew4 \bar{\ell }}$| for Ra = 104, 105, 106 and 107 as a function of |$\mathcal {P}$|. |${\skew4 \bar{\ell }}$| remains very close to 1 as long as |$\mathcal {P}$| is smaller than a transitional value |$\mathcal {P}_t\simeq 29$|. There is a rapid increase of |${\skew4 \bar{\ell }}_u$| above |$\mathcal {P}_t$|, showing the emergence of smaller scale convective modes at the transition between the translation mode and the high-|$\mathcal {P}$| regime. We interpret this sharp transition as being due to the negative feedback that the secondary flow and smaller scale convection have on the translation mode: advection of the potential temperature field by the secondary flow decreases the strength of its degree one component and therefore weakens the translation mode, which in turn give more time for smaller scale convection to develop, weakening further the degree one heterogeneity. The value of |$\mathcal {P}_t$| does not seem to depend on Ra in the range explored here. Fig. 6 further shows that ICB phase change has a strong influence on the flow up to |$\mathcal {P}\simeq 300$|, which is confirmed by direct visualization of the flow structure.
Mean degree |${\skew4 \bar{\ell }}_u$| of the kinetic energy (as defined in eq. 119), as a function of |$\mathcal {P}$|, for simulations with Ra = 104, 105, 106 and 107. The grey scale of the markers give the Rayleigh number of the simulation. |${\skew4 \bar{\ell }}_u$| is close to 1 for |$\mathcal {P}\lesssim 29$| for all Ra, although the departure from 1 increases with Ra when |$\mathcal {P}$| approaches 29 from below.
Fig. 7a shows the translation rate V (circles) and time averaged rms velocity (triangles) as a function of |$\mathcal {P}$| for various values of Ra. Here both V and Urms are multiplied by Ra−1/2. The grey dashed line shows the analytical prediction for the translation rate in the rigid inner core limit. Below |$\mathcal {P}_t$|, there is a good quantitative agreement between the numerical results and the analytical model. The fact that Urms ≃ V for |$\mathcal {P}<\mathcal {P}_t$| indicates that there is, as expected, negligible deformation in this regime. V and Urms diverge for |$\mathcal {P}>\mathcal {P}_t$|, the translation rate becoming rapidly much smaller than the rms velocity. As already suggested by the evolution of |${\skew4 \bar{\ell }}$|, phase change at the ICB has still an effect on the convection for |$\mathcal {P}$| up to ∼300. Phase change at the ICB has a positive feedback on the vigor of the convection: melting occurs preferentially above upwelling, where the dynamic topography is positive, which enhances upward motion. Conversely, solidification occurs preferentially above downwellings, thus enhancing downward motions. This effect becomes increasingly small as |$\mathcal {P}$| is increased, and the rms velocity reaches a plateau when |$\mathcal {P}\gtrsim 10^3$|, at which the effect of phase change at the ICB on the internal dynamics becomes negligible.
![(a) Rms velocity (triangles) and translation velocity (circles) as a function of $\mathcal {P}$, for Rayleigh numbers between 3 × 103 and 107 (grey scale). The inner core translation rate is found by first calculating the net translation rate Vi = x, y, z of the inner core in the directions x, y, z of a cartesian frame, given by the average over the volume of the inner core of the velocity component ui = x, y, z [which can be written as functions of the degree 1 components of the poloidal scalar at the ICB, see eq. (B42) in Appendix B]. We then write the global translation velocity as $V=\sqrt{V_x^2+V_y^2+V_z^2}$. The grey dashed line shows the prediction of the rigid inner core model. (b) ${\skew4 \dot{M}}\times Ra^{-1/2}$ as a function of $\mathcal {P}$, the grey scale of the markers giving the value of Ra. The grey dashed line shows the prediction of the rigid inner core model, showing excellent agreement between the theory and the numerical calculations for $\mathcal {P}$ small.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/gji/194/3/10.1093/gji/ggt202/3/m_ggt202fig7.jpeg?Expires=1716405506&Signature=B-S~6Beu4pe-IGBvhYlENVurjeEiHGwsJVfLeq1TTxpN6I2EQBCeu3J1CvXYJxQjjqQ~YYVgPK2dpo5KN27WUsr4cX7~U-KG8yJWrocbpDrPXKTdyEMJqcI5wWSKNfd81aQkgVRbfm1ZI~33zceXl1M4WUpZ42AdA6WGVCafkjstCP7d6-ItbyLTJI4yp9aHhIA0UW52OEaAVCVkBmWooWfCfGWLYTKd0Ouxzn6rzAoPv246lBzz9LF55gOAKvbY-w75IYVroopl8l1bpaXwB47GDmxlVLKGZhaztFVRnvlWMU-EMDeGoHceDLx~mkTu7INjEUR1ikSRSe5L6X713Q__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
(a) Rms velocity (triangles) and translation velocity (circles) as a function of |$\mathcal {P}$|, for Rayleigh numbers between 3 × 103 and 107 (grey scale). The inner core translation rate is found by first calculating the net translation rate Vi = x, y, z of the inner core in the directions x, y, z of a cartesian frame, given by the average over the volume of the inner core of the velocity component ui = x, y, z [which can be written as functions of the degree 1 components of the poloidal scalar at the ICB, see eq. (B42) in Appendix B]. We then write the global translation velocity as |$V=\sqrt{V_x^2+V_y^2+V_z^2}$|. The grey dashed line shows the prediction of the rigid inner core model. (b) |${\skew4 \dot{M}}\times Ra^{-1/2}$| as a function of |$\mathcal {P}$|, the grey scale of the markers giving the value of Ra. The grey dashed line shows the prediction of the rigid inner core model, showing excellent agreement between the theory and the numerical calculations for |$\mathcal {P}$| small.
Fig. 7(b) shows the rate of melt production (defined in eq. 117), multiplied by Ra−1/2, as a function of |$\mathcal {P}$| for various values of Ra. Again, the prediction of the rigid inner core model (eq. 116, grey dashed line in Fig. 7 b) is in very good agreement with the numerical results as long as |$\mathcal {P}<\mathcal {P}_t$|. For |$\mathcal {P}>\mathcal {P}_t$|, the rate of melt production appears to be inversally proportional to |$\mathcal {P}$|.
6.3 Scaling of translation rate, convective velocity and melt production
We now turn to a more quantitative description of the small-|$\mathcal {P}$| and large-|$\mathcal {P}$| regimes. We first compare the results of numerical simulations at |$\mathcal {P}<\mathcal {P}_t$| with the analytical models developed in Section 5. We then focus on the large-|$\mathcal {P}$| regime, and develop a scaling theory for inner core thermal convection in this regime, including a scaling law for the rate of melt production.
6.3.1 Translation mode
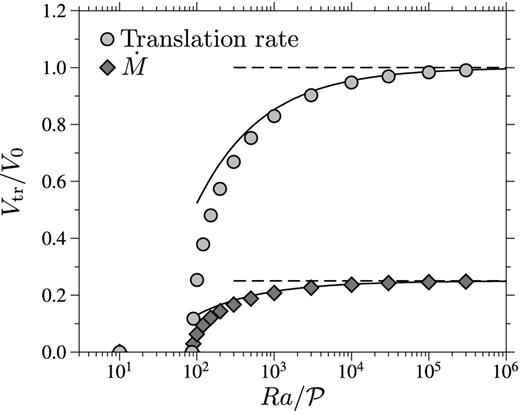
Fig. 8 shows the translation rate (circles) and the rate of melt production |${\skew4 \dot{M}}$| (diamonds), normalized by the rigid inner core estimate given by eq. (107), as a function of |$Ra/\mathcal {P}$|, for |$\mathcal {P}=10^{-2}$|. The translation rate increases from zero when |$Ra/\mathcal {P}$| is higher than a critical value |$(Ra/\mathcal {P})_c$| which is found to be in excellent agreement with the prediction of the linear stability analysis. Increasing |$Ra/\mathcal {P}$| above |$(Ra/\mathcal {P})_c$|, the translation rate increases before asymptoting towards the prediction of the rigid inner core model (dashed line). The prediction of our model including a boundary layer correction (eq. 115, black line in Fig. 8) is in good agreement with the numerical results for |$Ra/\mathcal {P}\gtrsim 10^3$|, demonstrating that our analytical model captures fairly well the effect of the thermal boundary layer. As expected (see Section 5.4), the rate of melt production is equal to 1/4 of the translation rate.
Translation rate and melt production, normalized by the low |$\mathcal {P}$| limit estimate given by eq. (107), as a function of |$Ra/\mathcal {P}$|, for |$\mathcal {P}=10^{-2}$|.
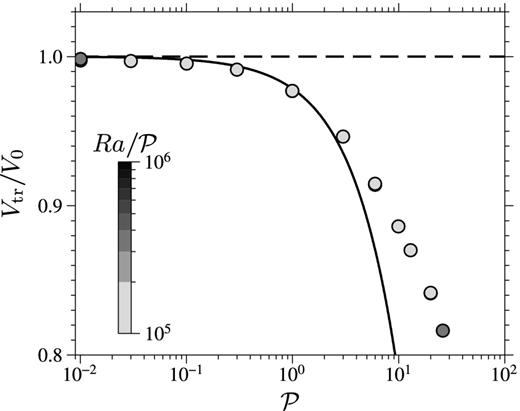
Fig. 9 shows the effect of increasing |$\mathcal {P}$| on the translation rate. In this figure, we have kept only simulations with |$Ra/\mathcal {P}$| larger than 105 to minimize the effect of the boundary layer, and further corrected the translation velocity with the boundary layer correction (eq. 115) found in Section 5.3, in order to isolate as much as possible the effect of |$\cal {P}$| on the translation mode. The |$\mathcal {O}(\mathcal {P})$| model developed in Section 5.2 (eq. 110, black line) agrees with the numerical simulations within 1 per cent for |$\mathcal {P}$| up to ∼3, but fails to explain the outputs of the numerical simulations when |$\mathcal {P}$| is larger, which indicates that higher order terms in |$\mathcal {P}$| become important.
Overall, our analytical results (stability analysis and finite amplitude models) are in very good agreement with our numerical simulations when |$\mathcal {P}$| is small, which gives support to both our theory and to the validity of the numerical code.
6.3.2 Plume convection
If |$\mathcal {P}$| is large, the translation rate of the inner core becomes vanishingly small, but, as long as |$\mathcal {P}$| is finite, there is still a finite rate of melt production associated with the smaller scale topography arising from plume convection. A scaling for the melt production in the limit of large |$\mathcal {P}$| and large Ra can be derived from scaling relationship for infinite Prandtl number convection with impermeable boundaries. Parmentier & Sotin (2000) derived a set of scaling laws for high Rayleigh number internally heated thermal convection in a cartesian box, in the limit of infinite Prandtl number, but we found significant deviations from their model in our numerical simulations, which we ascribe to geometrical effects due to the spherical geometry. We therefore propose a set of new scaling laws for convection in a full sphere with internal heating.
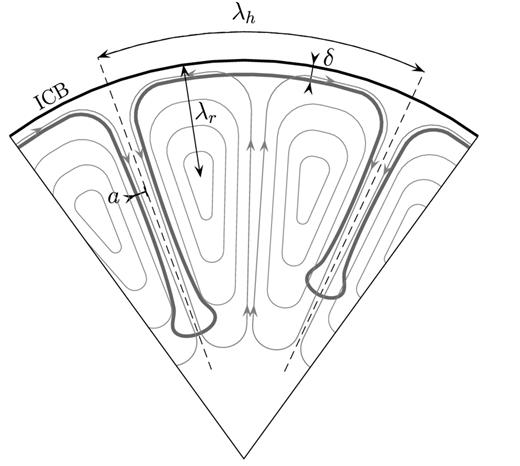
Quantities of interest are the horizontal and vertical velocities u and w, the mean inner core potential temperature 〈Θ〉, the thermal boundary layer thickness δ, the thermal radius of the plumes a, the average plume spacing λh, and a length scale for radial variations of the velocity, which we note λr (see Fig. 10). The horizontal length scale λh is related to the number N of plumes per unit area by |$N\sim 1/\lambda _h^2$|.
A schematic of inner core plume convection, and definition of the length scales used in the scaling analysis. Streamlines of the flow are shown with thin arrowed grey lines.
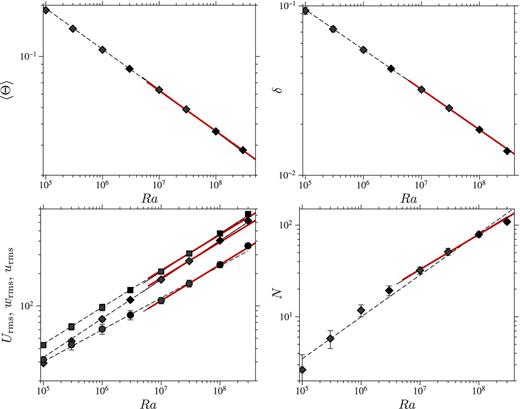
Outputs of numerical simulations (〈Θ〉, δ, rms velocity Urms, rms radial velocity wrms, rms horizontal velocity urms, N) are shown in Figs 11(a)–(d) for Ra between 105 and 3 × 108. The boundary layer thickness δ is estimated as the ratio of the mean potential temperature in the inner core, 〈Θ〉, over the time and space averaged potential temperature gradient at the ICB: δ = −〈Θ〉/〈∂Θ/∂r〉icb. The time-averaged number N of plume per unit area is estimated by counting plumes on horizontal surfaces on typically 50 different snapshots. Both 〈Θ〉 and δ follow well-defined power law behaviours over this range of Ra. In contrast, the rms velocities and plume density N seem to indicate a change of behaviour at Ra close to 107. For Ra < 107, the vertical velocity increases faster than the horizontal velocity, while at larger Ra horizontal and vertical velocities increase with Ra at roughly the same rate.
(a) Mean potential temperature 〈Θ〉 as a function of Ra for |$\mathcal {P}$| larger than 103. (b) Boundary layer thickness δ. (c) RMS velocity Urms (squares), rms vertical velocity wrms (diamonds), and rms horizontal velocity urms (circles). (d) Number of plumes N per unit surface. In figures (a) to (d), the thick red lines show the predictions of the scaling theory developed in Section 6.3.2 with β = −0.238. The dashed lines show the result of the individual least square inversion for each quantity for Ra ≥ 105.
The best fit of the numerical results (Figs 11a and b) gives 〈Θ〉 ∼ Ra−0.240 ± 0.005 and δ ∼ Ra−0.236 ± 0.003, in fair agreement with the predicted scaling. In Cartesian geometry, Parmentier & Sotin (2000) found β = −0.2448. Deschamps et al. (2012) found β = −0.238 for thermal convection in internally heated spherical shells.
This gives four eqs (122)–(125) for five unknowns (u, w, a, λh, λr). The system can be solved if additional assumptions are made on the scaling of λr. For high Pr, low Re convection, a natural choice would be to assume that radial variations of w occur at the scale of the radius of the inner core. This implies λr ∼ 1, and solving the system of eqs (122)–(125) with β = −0.24 gives a ∼ Ra−0.14, u ∼ Ra0.82, w ∼ Ra0.72 and N ∼ Ra−0.2, which agrees very poorly with the numerical results.
Assuming a scaling of the form given by eqs (126)–(128), it is possible to inverse simultaneously all variables for β, the result of the inversion being β = −0.238 ± 0.003 (±1σ). The prediction of eqs (126)–(128) with this value of β are shown with red lines in Fig. 11a–d for Ra ≥ 107. They agree with the numerical outputs almost as well as individual inversions, which demonstrates the self-consistency of our scaling theory.
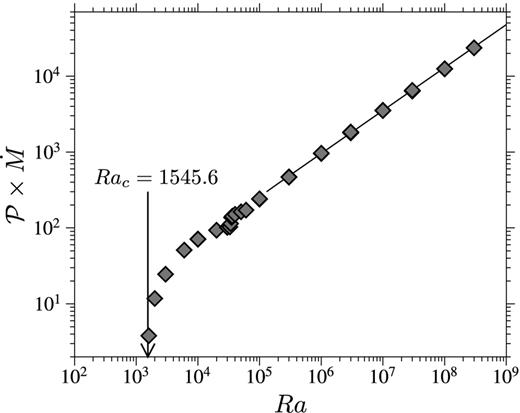
Fig. 12(b) shows |$\mathcal {P} {\skew4 \dot{M}}$| as a function of Ra, for |$\mathcal {P}\ge 10^3$| corresponding to the plume convection regime. There is an almost perfect collapse of the data points, which supports the fact that |${\skew4 \dot{M}} \propto \mathcal {P}$| in this regime. The kink in the curve at Ra ≃ 3 × 104 corresponds to the transition from steady convection to unsteady convection. Above this transition, the data points are well fitted by a power law of the form |${\skew4 \dot{M}} =a \mathcal {P}^{-1} Ra^{b}$|. Least-square regression for Ra ≥ 3 × 105 gives a = 0.46 ± 0.04 and b = 0.554 ± 0.006, in reasonable agreement with the value found above. In dimensional terms, |${\skew4 \dot{M}} \simeq a ({\kappa }/{r_\mathrm{ic}}) \mathcal {P}^{-1}Ra^{b}$| and the mass flux of molten material is |$\rho _\mathrm{ic} {\skew4 \dot{M}} \simeq a {k}/({c_p r_\mathrm{ic}}) \mathcal {P}^{-1}Ra^{b}$|.
Rate of melt production (multiplied by |$\mathcal {P}$|) as a function of Ra, for numerical simulations with |$\mathcal {P} \ge 10^3$|. The value of the critical Rayleigh number as predicted by the linear stability analysis in the limit of infinite |$\mathcal {P}$| (eq. 89, Rac = 1545.6) is indicated by the arrow.
7 APPLICATION
7.1 Evolutive models
The analytical model for the translation mode and the scaling laws for large-|$\mathcal {P}$| convection derived in the previous sections strictly apply only to convection with ric and S constant. We therefore first check that our models correctly describe inner core convection when ric and S are time-dependent, by comparing their predictions with the outcome of numerical simulations with inner core growth and thermal history determined from the core energy balance.
Correspondence between τic and |$\mathcal {T}_\mathrm{ic}$| for three values of inner core thermal conductivity, assuming dTs/dTad = 1.65 ± 0.11 (Deguen & Cardin 2011).
| k (W m−1 K−1) | ||||
|---|---|---|---|---|
| 36 | 79 | 150 | ||
| 0.8 | 1.18 ± 0.23 Gy | 0.54 ± 0.11 Gy | 0.28 ± 0.06 Gy | |
| |${\mathcal {T}_\mathrm{ic}}=$| | 1.0 | 1.48 ± 0.29 Gy | 0.68 ± 0.13 Gy | 0.36 ± 0.07 Gy |
| 1.2 | 1.77 ± 0.35 Gy | 0.81 ± 0.16 Gy | 0.43 ± 0.08 Gy |
| k (W m−1 K−1) | ||||
|---|---|---|---|---|
| 36 | 79 | 150 | ||
| 0.8 | 1.18 ± 0.23 Gy | 0.54 ± 0.11 Gy | 0.28 ± 0.06 Gy | |
| |${\mathcal {T}_\mathrm{ic}}=$| | 1.0 | 1.48 ± 0.29 Gy | 0.68 ± 0.13 Gy | 0.36 ± 0.07 Gy |
| 1.2 | 1.77 ± 0.35 Gy | 0.81 ± 0.16 Gy | 0.43 ± 0.08 Gy |
Correspondence between τic and |$\mathcal {T}_\mathrm{ic}$| for three values of inner core thermal conductivity, assuming dTs/dTad = 1.65 ± 0.11 (Deguen & Cardin 2011).
| k (W m−1 K−1) | ||||
|---|---|---|---|---|
| 36 | 79 | 150 | ||
| 0.8 | 1.18 ± 0.23 Gy | 0.54 ± 0.11 Gy | 0.28 ± 0.06 Gy | |
| |${\mathcal {T}_\mathrm{ic}}=$| | 1.0 | 1.48 ± 0.29 Gy | 0.68 ± 0.13 Gy | 0.36 ± 0.07 Gy |
| 1.2 | 1.77 ± 0.35 Gy | 0.81 ± 0.16 Gy | 0.43 ± 0.08 Gy |
| k (W m−1 K−1) | ||||
|---|---|---|---|---|
| 36 | 79 | 150 | ||
| 0.8 | 1.18 ± 0.23 Gy | 0.54 ± 0.11 Gy | 0.28 ± 0.06 Gy | |
| |${\mathcal {T}_\mathrm{ic}}=$| | 1.0 | 1.48 ± 0.29 Gy | 0.68 ± 0.13 Gy | 0.36 ± 0.07 Gy |
| 1.2 | 1.77 ± 0.35 Gy | 0.81 ± 0.16 Gy | 0.43 ± 0.08 Gy |
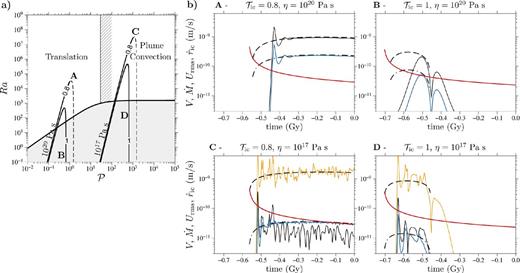
Fig. 13(a) shows the trajectories of the inner core state in a |$Ra-\mathcal {P}$| space for four different scenarios, superimposed on a regime diagram for inner core thermal convection. According to eq. (6), the ICB phase change timescale scales as |$\tau _\phi \propto r_\mathrm{ic}^{-1}$|, and therefore |$\mathcal {P}\propto r_\mathrm{ic}$| always increases during inner core history. In contrast, the evolution of Ra(t) is non monotonic, with the effect of the increasing inner core radius and gravity opposing the decrease with time of the effective heating rate S(t). Because S eventually becomes negative at some time in inner core history, Ra reaches a maximum before decreasing and eventually becoming negative, resulting in a bell shaped trajectory of the inner core in the |$Ra-\mathcal {P}$| space. The maximum in Ra may or may not have been reached yet, depending on the value of |$\mathcal {T}_\mathrm{ic}$|.
(a) Trajectories of the inner core state in a |$Ra-\mathcal {P}$| space, for the four cases A, B, C and D discussed in the text. The line annotations give the value of |$\mathcal {T}_\mathrm{ic}$| for each case. The dashed lines shows the future trajectory of the inner core. (b) Time evolution of V, |${\skew4 \dot{M}}$|, Urms and |$\dot{r}_\mathrm{ic}$| for cases A to D. Red line: inner core growth rate |$\dot{r}_\mathrm{ic}$|. Black line: translation rate V. Orange line-: rms velocity Urms. Blue line: dimensional melting rate |$(\kappa /r_\mathrm{ic}){\skew4 \dot{M}}$|. Predictions for the rms velocity (or translation velocity in the translation regime) and melting rate |${\skew4 \dot{M}}$| are shown with thick dashed and dash-dotted lines, respectively. In the η = 1020 Pa s cases, the translation model (eq. 115) is used to predict V and |${\skew4 \dot{M}}$|. In the η = 1017 Pa s case, the high-|$\mathcal {P}$| scaling is used for Urms and |${\skew4 \dot{M}}$|. In the η = 1020 Pa s, |$\mathcal {T}_\mathrm{ic}=0.8$| and |$\mathcal {T}_\mathrm{ic}=1$| cases, the translation rate and the rms velocity are equal. For these simulations, the Rayleigh number was calculated assuming a thermal conductivity k = 79 W m−1 K−1 and a phase change timescale τϕ = 1000 yr. Values of other physical parameters used for these runs are summarized in Table 1.
The scenarios A--D shown in Fig. 13a have been chosen to illustrate four different possible dynamic histories of the inner core. In cases A and C, which have |$\mathcal {T}_\mathrm{ic}=0.8$|, Ra remains positive and supercritical up to today, thus always permitting thermal convection. In cases B and D, which have |$\mathcal {T}_\mathrm{ic}=1$|, Ra has reached a maximum early in inner core history, before decreasing below supercriticality, at which point convection is expected to stop. In these two cases, only an early convective episode is expected (Buffett 2009; Deguen & Cardin 2011). In cases A and B, which have η = 1020 Pa s, |$\mathcal {P}(t)$| is always smaller than the transitional |$\mathcal {P}_t$| and thermal convection therefore should be in the translation regime; Cases C and D, which have η = 1017 Pa s, have |$\mathcal {P}(t)>10^2>\mathcal {P}_t$| and thermal convection should be in the plume regime.
Fig. 13(b) shows outputs from numerical simulations corresponding to the inner core histories shown in Fig. 13(a). The numerical results are compared to the predictions for the rms velocity Urms (equal to the translation rate Vtr in the translation regime) and melting rate |${\skew4 \dot{M}}$| from the analytical translation model (eq. 116) and the large-|$\mathcal {P}$| scaling laws (eq. 133). The agreement is good in both the translation and plume convection regimes, except at the times of initiation and cessation of convection.
In cases B and D, the flow occurring after t ≃ −0.46 Gy, at a time where the models predict no motion (because S < 0), corresponds to a slow relaxation of the thermal heterogeneities left behind by the convective episode.
Apart during the initiation and cessation periods of convection, the models developed for steady internal heating and constant inner core radius agree very well with the full numerical calculations, and can therefore be used to predict the dynamic state of the inner core and key quantities including rms velocity and melt production rate.
7.2 Melt production
Experiments by Alboussière et al. (2010) have shown that the development of a stably stratified layer above the ICB by inner core melting is controlled by the ratio ΦB of the buoyancy fluxes arising from the melting and freezing regions of the ICB. By using the analytical translation model and the scaling laws for plume convection developed in the last two sections, we can now estimate today's value of ΦB as a function of the state and physical properties of the inner core, and assess the likelihood of the origin of the F-layer by inner core melting.
7.3 Today's inner core regime and rate of melt production
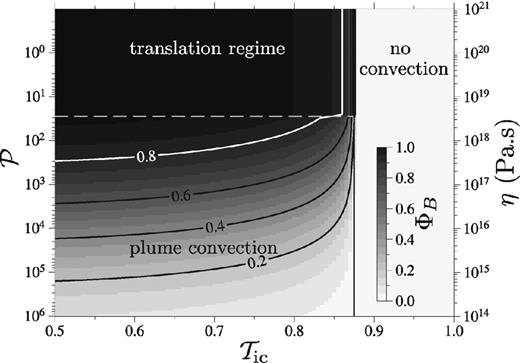
Inner core regime diagram and map of the buoyancy ratio ΦB, as functions of |$\mathcal {P}$| and |$\mathcal {T}_\mathrm{ic}$|. The corresponding values of η assuming τϕ = 1000 yr are given on the right hand size vertical axis. According to Alboussière et al. (2010)'s experiments, inner core melting can produce a stably stratified layer at the base of the outer core if ΦB > 0.8 (white contour).
The inner core has currently an unstable thermal profile only if |$\mathcal {T}_\mathrm{ic}$| is smaller than ≃0.87. The mode of thermal convection then depends on |$\mathcal {P}$|, with the translation regime (small |$\mathcal {P}$|) being the most efficient at producing melt. Plume convection generates less melt, but the rate of melt production still remains significant as long as |$\mathcal {P}$| is not too large (η not too small). The critical value of ΦB = 0.8 (white contour in Fig. 14) suggested by the experiments of Alboussière et al. (2010) is almost always reached in the translation regime, but only in a small part of the parameter space in the plume convection regime.
8 COMPOSITIONAL EFFECTS
We have so far left aside the possible effects of the compositional evolution of the outer and inner core on the inner core dynamics. We will argue here that the development of an iron rich layer above the inner core can have a possibly important positive feedback on inner core convection: irrespectively of the exact mechanism at the origin of the F-layer (Gubbins et al.2008, 2011; Alboussière et al.2010), its interpretation as an iron rich layer implies a decrease with time of light elements concentration in the liquid just above the ICB. This in turn implies that the newly crystallized solid is increasingly depleted in light elements, and intrinsically denser, which may drive compositional convection in the inner core. The reciprocal coupling between the inner core and the F-layer may create a positive feedback loop which can make the system (inner core + F-layer) unstable. The mechanism releases more gravitational energy than purely radial inner core growth with no melting, and should therefore be energetically favored.
There is an additional feedback, this time negative, which comes from the effect of composition on the solidification temperature, which increases with decreasing light element concentration. The decreasing light element concentration at the base of the F-layer implies that the ICB temperature decreases with time at a slower rate than if the composition is fixed, which results in a smaller effective heating rate S (eq. 30). For a fixed inner core growth rate, this decreases the ICB cooling rate by an amount equal to |$-m_c \, \dot{c}_\mathrm{icb}^l$|, where mc = ∂Ts/∂c ∼ −104 K (Alfè et al.2002) is the liquidus slope at the inner core boundary pressure and composition. This adds a term |$-\alpha \, m_c \, \dot{c}_\mathrm{icb}^l$| in eq. (146). If only one light element is considered, the ratio of the stabilizing term |$\alpha \, m_c \, \dot{c}_\mathrm{icb}^l$| over the destabilizing term |$-\alpha _c\, k\, \dot{c}_\mathrm{icb}^l$| is ∼α mc/(αc k) ∼ −0.1/k. The two terms are of the same order of magnitude if k ∼ 0.1, but the negative feedback dominates if k is smaller.
The above estimates are clearly uncertain, and a dynamic model of the F-layer will be required for assessing in a self-consistent way the effect of the development of the F-layer on inner core convection. There are several feedbacks of the formation of an F-layer on inner core convection, either positive or negative, and it is not clear yet whether the net effect would be stabilizing or destabilizing. Still, it does suggest that the effect could be important, and worth considering in more details.
9 SUMMARY AND CONCLUSIONS
Inner core translation can potentially explain a significant part of the inner core structure, but its existence depends critically on the value of a number of poorly constrained parameters. In this paper, we have studied in details the conditions for and dynamics of inner core thermal convection when melting and solidification at the ICB are allowed. We summarize here the main results and implications of our work:
If the inner core is convectively unstable, linear stability analysis (Section 4), asymptotic calculations (Section 5), and direct numerical simulations (Section 6) consistently show that the convection regime depends mostly on a non-dimensional number, the ‘phase change number’ |$\mathcal {P}$|, characterizing the resistance to phase change (eq. 58). The convective translation mode dominates only if |$\mathcal {P}<29$|, which requires that the inner core viscosity is larger than a critical value estimated to be ∼3 × 1018 Pa s. If |$\mathcal {P}$| is larger (smaller viscosity), melting and solidification at the ICB have only a small dynamic effect, and convection takes the usual form of low Prandtl number internally heated convection, with a one-cell axisymmetric mode at the onset, and chaotic plume convection if the Rayleigh number is large.
With published estimates of the inner core viscosity ranging from 1011 to 1022 Pa s (Yoshida et al.1996; Buffett 1997; Van Orman 2004; Mound & Buffett 2006; Koot & Dumberry 2011; Reaman et al.2011, 2012), the question of which mode would be preferred is open (although we note that the latest estimate from mineral physics, 1020–1022 Pa s (Reaman et al.2012), would put the inner core, if unstably stratified, well within the translation regime).
The two convection regimes have been characterized in details in Sections 4–7; a summary of theoretical results and scaling laws for useful dynamic quantities (rms velocity, rate of melt production, mean potential temperature, number of plumes per unit area, and strain rate) is given in Table 3. If the inner core is unstably stratified, the rate of melt production predicted by our models is always large enough to produce an iron-rich layer at the base of the outer, according to Alboussière et al. (2010)'s experiments, if the inner core is in the translation regime (Fig. 14). In the plume convection regime, the rate of melt production can still be significant if |$\mathcal {P}$| is not too large (η not too small).
Being driven by buoyancy, a prerequisite for the existence of convective translation is that an unstable density profile is maintained within the inner core. Thermal convection requires that a superadiabatic temperature profile is maintained with the inner core, which is highly dependent on the core thermal history and inner core thermal conductivity. With k = 36 W m−1 K−1 as proposed by Stacey & Davis (2008), this would be very likely (Buffett 2009; Deguen & Cardin 2011). However, several independent groups (Sha & Cohen 2011; de Koker et al.2012; Pozzo et al.2012) have recently argued for a much higher core thermal conductivity, around 150 W m−1 K−1 or higher. This would make thermal convection in the inner core, whether in the translation mode or in the plume convection mode, impossible unless the inner core is very young (≃300 Myr or less, which would require a probably excessively high CMB heat flux).
Compositional convection might be a viable alternative to thermal convection, either because the temperature dependency of the light elements partitioning behaviour can produce an unstable compositional profile (Gubbins et al.2013), or because of a possibly positive feedback of the development of the F-layer on inner core convection. As proposed in Section 8, the formation of an iron-rich layer at the base of the outer core over the history of the inner core implies that the inner core crystallizes from a source which is increasingly depleted in light elements. This in turn implies that the newly crystallized solid is increasingly depleted in light element, which results in an unstable density profile. Whether this positive feedback is strong enough to overcome the stabilizing effect of a possibly subadiabatic temperature profile depends on the dynamics of the F-layer, and further work is needed to test this idea.
Summary of theoretical results and scaling laws for the translation (|$\mathcal {P} \lesssim 29$|) and plume convection (|$\mathcal {P} \gg 29$|) regimes. In the plume convection regime, the value of β obtained by fitting the numerical outputs to our scaling theory is β = −0.238 ± 0.003.
| Translation regime | Plume convection regime | |
|---|---|---|
| |$\mathcal {P} \lesssim 29$| | |$\mathcal {P} \gg 29$| | |
| Onset | |$(\frac{Ra}{\mathcal {P}})_{c} = \frac{175}{2}$| | Rac = 1545.6 |
| Velocity scaling , V or Urms | |$\frac{\kappa }{r_\mathrm{ic}} \sqrt{\frac{6}{5}\frac{Ra}{\mathcal {P}}}$| | |$0.96 \frac{\kappa }{r_\mathrm{ic}} Ra^{2+7\beta }$| |
| Rate of melt production, |${\skew4 \dot{M}}$| | |$\frac{1}{4}\frac{\kappa }{r_\mathrm{ic}} \sqrt{\frac{6}{5}\frac{Ra}{\mathcal {P}}}$| | |$0.46\frac{\kappa }{r_\mathrm{ic}} Ra^{1+2\beta } \mathcal {P}^{-1}$| |
| 〈Θ〉 | |$\frac{S r_\mathrm{ic}^2}{\kappa } (\frac{10}{3}\frac{\mathcal {P}}{Ra})^{1/2}$| | |$2.9 \frac{S r_\mathrm{ic}^2}{\kappa } Ra^\beta$| |
| Number of plumes per unit area, N | – | |$\frac{0.07}{r_\mathrm{ic}^2} Ra^{-2-10\beta }$| |
| Strain rate |$\dot{\epsilon }\sim \frac{U_\mathrm{rms}}{\lambda } \sim \sqrt{N} U_\mathrm{rms}$| | – | |$0.25 \frac{\kappa }{r_\mathrm{ic}^2} Ra^{1+2\beta }$| |
| Translation regime | Plume convection regime | |
|---|---|---|
| |$\mathcal {P} \lesssim 29$| | |$\mathcal {P} \gg 29$| | |
| Onset | |$(\frac{Ra}{\mathcal {P}})_{c} = \frac{175}{2}$| | Rac = 1545.6 |
| Velocity scaling , V or Urms | |$\frac{\kappa }{r_\mathrm{ic}} \sqrt{\frac{6}{5}\frac{Ra}{\mathcal {P}}}$| | |$0.96 \frac{\kappa }{r_\mathrm{ic}} Ra^{2+7\beta }$| |
| Rate of melt production, |${\skew4 \dot{M}}$| | |$\frac{1}{4}\frac{\kappa }{r_\mathrm{ic}} \sqrt{\frac{6}{5}\frac{Ra}{\mathcal {P}}}$| | |$0.46\frac{\kappa }{r_\mathrm{ic}} Ra^{1+2\beta } \mathcal {P}^{-1}$| |
| 〈Θ〉 | |$\frac{S r_\mathrm{ic}^2}{\kappa } (\frac{10}{3}\frac{\mathcal {P}}{Ra})^{1/2}$| | |$2.9 \frac{S r_\mathrm{ic}^2}{\kappa } Ra^\beta$| |
| Number of plumes per unit area, N | – | |$\frac{0.07}{r_\mathrm{ic}^2} Ra^{-2-10\beta }$| |
| Strain rate |$\dot{\epsilon }\sim \frac{U_\mathrm{rms}}{\lambda } \sim \sqrt{N} U_\mathrm{rms}$| | – | |$0.25 \frac{\kappa }{r_\mathrm{ic}^2} Ra^{1+2\beta }$| |
|$Ra = \frac{\alpha \rho _s g_\mathrm{icb} S r_\mathrm{ic}^5 }{6 \kappa ^2 \eta }$|, |${\cal {P}} = \frac{\Delta \rho \, g_\mathrm{icb} \, r_\mathrm{ic} \, \tau _\phi }{\eta }$|.
Summary of theoretical results and scaling laws for the translation (|$\mathcal {P} \lesssim 29$|) and plume convection (|$\mathcal {P} \gg 29$|) regimes. In the plume convection regime, the value of β obtained by fitting the numerical outputs to our scaling theory is β = −0.238 ± 0.003.
| Translation regime | Plume convection regime | |
|---|---|---|
| |$\mathcal {P} \lesssim 29$| | |$\mathcal {P} \gg 29$| | |
| Onset | |$(\frac{Ra}{\mathcal {P}})_{c} = \frac{175}{2}$| | Rac = 1545.6 |
| Velocity scaling , V or Urms | |$\frac{\kappa }{r_\mathrm{ic}} \sqrt{\frac{6}{5}\frac{Ra}{\mathcal {P}}}$| | |$0.96 \frac{\kappa }{r_\mathrm{ic}} Ra^{2+7\beta }$| |
| Rate of melt production, |${\skew4 \dot{M}}$| | |$\frac{1}{4}\frac{\kappa }{r_\mathrm{ic}} \sqrt{\frac{6}{5}\frac{Ra}{\mathcal {P}}}$| | |$0.46\frac{\kappa }{r_\mathrm{ic}} Ra^{1+2\beta } \mathcal {P}^{-1}$| |
| 〈Θ〉 | |$\frac{S r_\mathrm{ic}^2}{\kappa } (\frac{10}{3}\frac{\mathcal {P}}{Ra})^{1/2}$| | |$2.9 \frac{S r_\mathrm{ic}^2}{\kappa } Ra^\beta$| |
| Number of plumes per unit area, N | – | |$\frac{0.07}{r_\mathrm{ic}^2} Ra^{-2-10\beta }$| |
| Strain rate |$\dot{\epsilon }\sim \frac{U_\mathrm{rms}}{\lambda } \sim \sqrt{N} U_\mathrm{rms}$| | – | |$0.25 \frac{\kappa }{r_\mathrm{ic}^2} Ra^{1+2\beta }$| |
| Translation regime | Plume convection regime | |
|---|---|---|
| |$\mathcal {P} \lesssim 29$| | |$\mathcal {P} \gg 29$| | |
| Onset | |$(\frac{Ra}{\mathcal {P}})_{c} = \frac{175}{2}$| | Rac = 1545.6 |
| Velocity scaling , V or Urms | |$\frac{\kappa }{r_\mathrm{ic}} \sqrt{\frac{6}{5}\frac{Ra}{\mathcal {P}}}$| | |$0.96 \frac{\kappa }{r_\mathrm{ic}} Ra^{2+7\beta }$| |
| Rate of melt production, |${\skew4 \dot{M}}$| | |$\frac{1}{4}\frac{\kappa }{r_\mathrm{ic}} \sqrt{\frac{6}{5}\frac{Ra}{\mathcal {P}}}$| | |$0.46\frac{\kappa }{r_\mathrm{ic}} Ra^{1+2\beta } \mathcal {P}^{-1}$| |
| 〈Θ〉 | |$\frac{S r_\mathrm{ic}^2}{\kappa } (\frac{10}{3}\frac{\mathcal {P}}{Ra})^{1/2}$| | |$2.9 \frac{S r_\mathrm{ic}^2}{\kappa } Ra^\beta$| |
| Number of plumes per unit area, N | – | |$\frac{0.07}{r_\mathrm{ic}^2} Ra^{-2-10\beta }$| |
| Strain rate |$\dot{\epsilon }\sim \frac{U_\mathrm{rms}}{\lambda } \sim \sqrt{N} U_\mathrm{rms}$| | – | |$0.25 \frac{\kappa }{r_\mathrm{ic}^2} Ra^{1+2\beta }$| |
|$Ra = \frac{\alpha \rho _s g_\mathrm{icb} S r_\mathrm{ic}^5 }{6 \kappa ^2 \eta }$|, |${\cal {P}} = \frac{\Delta \rho \, g_\mathrm{icb} \, r_\mathrm{ic} \, \tau _\phi }{\eta }$|.
We would like to thank the two anonymous referees for many helpful comments and suggestions. All the computations presented in this paper were performed at the Service Commun de Calcul Intensif de l’Observatoire de Grenoble (SCCI). RD was supported by grant EAR-0909622 and Frontiers in Earth System Dynamics grant EAR-1135382 from the National Science Foundation. TA was supported by the ANR (Agence National de la Recherche) within the CrysCore project ANR-08-BLAN-0234-01, and by the program PNP of INSU/CNRS. PC was supported by the program PNP of INSU/CNRS.
REFERENCES
APPENDIX A: LINEAR STABILITY ANALYSIS
We investigate here the linear stability of the system of equations describing thermal convection in the inner core with phase change at the ICB, as derived in Section 3. The calculation given here is a generalization of the linear stability analysis of thermal convection in an internally heated sphere given by Chandrasekhar (1961).
APPENDIX B: TRANSLATION RATE AT |$\mathcal {O}(\mathcal {P})$|
In order to estimate the translation velocity at |$\mathcal {O}(\mathcal {P})$|, we need to determine the parameter A in the |$\mathcal {O}(\mathcal {P})$| expansion of p1 (eq. 101), which was left undetermined. To do so, we need to consider the thermal field at |$\mathcal {O}(\mathcal {P})$| and the velocity field at |$\mathcal {O}(\mathcal {P}^2)$|. This is more challenging because, owing to the non-linearity of the heat equation, coupling of higher order components of the temperature and velocity fields contribute to the l = 1 component of the temperature field at |$\mathcal {O}(\mathcal {P})$|, and to the l = 1 component of the velocity field at |$\mathcal {O}(\mathcal {P}^2)$|.
B1 l = 2 components of the thermal field and velocity field
We now calculate the l = 2 component of the temperature field at zeroth order in |$\mathcal {P}$|, which will then be used to find the l = 2 component of the velocity field at |$\mathcal {O}(\mathcal {P})$|.
