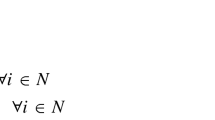Need to Meet Investment Goals? Track Synthetic Indexes with the SDDP Method

Abstract

This work presents a novel application of the Stochastic Dual Dynamic Problem (SDDP) to large-scale asset allocation. We construct a model that delivers allocation policies based on how the portfolio performs with respect to user-defined (synthetic) indexes, and implement it in a SDDP open-source package. Based on US economic cycles and ETF data, we generate Markovian regime-dependent returns to solve an instance of multiple assets and 28 time periods. Results show our solution outperforms its benchmark, in both profitability and tracking error.

1 Objectives and Contributions

Multistage stochastic programming (MSP) is a well-known framework for modeling large-scale problems under uncertainty, and has been widely used in several fields, including asset allocation problems.¹ MSP solutions have the quality of enabling planning not only for today’s positions, but also for future portfolio rebalancing, depending on the evolution of market events and prices. That advantage avoids increases in turnover (which leads to higher transaction costs) and augment the probability of meeting objectives by measuring them under possible future outcomes.

One of the main complexities of solving MSP is known as the “curse of dimensionality”, which happens when working with a high-dimensional state space. In this case, it becomes intractable to find the optimal solution by computing the Bellman function in each state. The number of possible allocations and scenarios to consider for future asset prices increases exponentially with the time horizon, or more specifically, to the number of rebalancing periods. Thus, high dimensionality is present in both, long-term asset and liability management (ALM) problems and short-term problems with frequent rebalancing.

Pereira and Pinto (1991) propose a method for handling large-scale MSP, called the Stochastic Dual Dynamic Problem (SDDP). The SDDP approximates the Bellman function of the dynamic programming model with linear cuts, instead of computing its exact value in every state. This method has mainly been used in electricity generation planning and the extraction of natural resources. However, its use in financial applications is recent and incipient.

In this paper, we show how the SDDP can be applied to a particular asset allocation problem. We implement a model that allows the inclusion of transaction costs, short-selling and time-dependent returns in the Julia SDDP.jl package created by Dowson and Kapelevich (2017). In this way, we illustrate how one might work with the SDDP without needing to build the method from scratch, as happened before the irruption of open-source programming languages. We also solve an instance involving 28 rebalancing periods, which to the best of our knowledge, no other research has done before with the SDDP method.

The objective of our model is to generate dynamic allocation policies that aim to achieve user-defined goals, rather than maximizing profits or the expected utilities of investors’ wealth as previous studies do. This approach might be suitable for pension fund managers that must meet future pension commitments, or insurance companies that must cover insurance claims. Wealthy investors or non-profit institutions with big endowments (e.g. universities) might prefer stable returns over time, even if this comes with lower expected profits in the long term.

We also propose a novel multistage stochastic dynamic programming model using the idea of index tracking as a way to achieve managers’ goals. For this reason, the allocation strategy aims to track user-defined indexes, rather than a real index, as previous studies do. Our allocation policies are not intended to reduce the error experienced with common tracking measures. Instead, we follow the idea of previous research solving the Enhanced Index Tracking Problem (EITP), so as to outperform the index. In our study, we do this by tracking the negative deviations of the cumulative returns of the replicating portfolio. Figure 1 illustrates how tracking cumulative returns differs from following one-period returns. Suppose the goal is to replicate an index with a fixed return of r at each time period. If the cumulative returns are below those of the index (case A), then the portfolio needs to achieve a return that is higher than r in the following periods, in order to track the cumulative returns of the index. The opposite happens when the cumulative returns are above those of the index (case B). In this case, the portfolio can afford to achieve returns that are lower than r, as long as the cumulative returns remain higher than those of the index.

The paper is structured as follows. In the next section, we provide a brief literature review related to applications of the SDDP method and the index tracking problem. In Sect. 3, we explain the SDDP method and the proposed model for tracking predefined returns. Then, in Sect. 4, we test and analyze the performance of the model based on market data involving 6 assets and 28 rebalancing periods (7 years with quarterly rebalancing). Finally, we discuss the main conclusion and possible improvements that can be made in future research.

Fig. 1

Tracking an index with constant one-period return r. A and B represent cases where the cumulative returns of the portfolio are below and above those of the index respectively. Our tracking measure only considers negative deviations from the cumulative returns of the index (case A)

2 Literature Review

As stated previously, the SDDP method has mostly been used in electricity generation planning. For example, Pereira and Pinto (1991), Guigues (2014) and Soares et al. (2017) plan the generation of hydro-thermal plants under climate (water resource) uncertainty. It has also been applied in electricity distribution and energy storage, such as in Bhattacharya et al. (2016), where uncertainty comes from consumption and generation. The SDDP is also implemented in supply chain problems (e.g. Fhoula et al. (2013)), where acquisition, storage and routing decisions must be planned ahead given possible disruption throughout the chain. In the mining industry, Reus et al. (2019) provide a dynamic policy for storing and selling ore under production and price uncertainty.

Kozmík and Morton (2015) is one of the first studies to employ the SDDP in asset allocation problems. Its main contribution is to implement the algorithm for this financial application, rather than focusing on the sophistication of the asset price (return) model or portfolio rules. This implementation includes risk measures within the objective function. Dupačová and Kozmík (2017) improve the efficiency of the algorithm by reducing the number of scenarios needed for asset returns. However, it does not include transaction costs or stage-dependent uncertainty. One of the most complete models using the SDDP is the one proposed in Valladão et al. (2019), which can handle the selection of many assets including trading costs. It also includes risk constraints and Markovian time-dependent returns based on a factor model and regimes. Our work differs from previous studies in the objective driving the allocation decisions. We propose a model that aims tracking an index to obtain steady returns, instead of maximizing the compromise between profits and risk. As we will see in Sect. 3.2, this change in goal necessitates building a different model, with different variables and constraints. Our work can also solve a model with more stages, as compared for instance to Valladão et al. (2019), which solve problems with up to 12 time periods.

In terms of the EITP, Canakgoz and Beasley (2009), Guastaroba et al. (2016) and Gnägi and Strub (2020) propose mixed integer programming models which can handle asset selection over a pool of assets and allocation simultaneously. They have the flexibility to include many types of investor requirements and objective functions, including transaction costs and liquidity constraints, among others. The drawback of these models is that they use a one-stage framework and no stochastic behavior in the investment opportunity set.

With respect to continuous-time models, such as those in Koijen et al. (2009), Munk and Sorensen (2010), and Bick et al. (2013), the portfolio is chosen simultaneously with income and consumption decisions, and they aim maximizing the expected utility of investors’ wealth. Browne (2013) and Agarwal and Sircar (2018) are two of the few works focusing on index tracking. One drawback of the continuous-time approach is that they can be solved analytically only under certain assumptions and conditions, like in the case of Browne (2013). Problems with reality-based portfolio rules have to be solved with numerical methods, and thus their resolution also depends on the dimensionality of the state space, just like in a discrete setting.

3 Methodology

3.1 SDDP Method

The SDDP is a numerical method that solves multistage stochastic dynamic programming problems. Decisions in this type of problems are planned for each time period, depending on the realization of uncertainty over time. The dynamic programming structure decomposes the model into time-dependent subproblems, and thus facilitates the search for the optimal solution. For illustrative purposes, let $x_t$ denote the decisions at each time period t, and let $\xi _t$ be the stochastic process, which is exogenous to the decision maker. Each subproblem can be written recursively, as in Philpott and De Matos (2012).

For $t=1:$

$$\begin{aligned} \begin{aligned} z =\min _{x_1 \ge \ \ell _1}\ \ c_1 x_1 + {\mathbb {E}}[Q_{2}(x_{1},\xi _{2})] \\ \text {subject to:} \quad A_1 x_1 = b_1 - B_1 x_{0} \\ \end{aligned} \end{aligned}$$

(1)

For $t=2,\ldots ,T$:

$$\begin{aligned} \begin{aligned} Q_t(x_{t-1},\xi _{t}) =\min _{x_t\ge \ \ell _t}\ \ c_t x_t +{\mathbb {E}}[Q_{t+1}(x_{t},\xi _{t+1})] \\ \text {subject to:} \quad A_t x_t = b_t - B_t x_{t-1} \\ \end{aligned} \end{aligned}$$

(2)

Matrix $B_t$ and vector $b_t$ are affected by $\xi _t$, while $A_t$ and $c_t$ are not. This formulation includes the known “non-anticipativity constraints”, that is, the $x_t$ are obtained without knowing the values of $\xi _l \ \forall l>t$. In the last time period, we assume that ${\mathbb {E}}[Q_{T+1}(x_{T},\xi _{T+1})]=0$ or a convex function defining the expected costs after horizon T.

As we have discussed, the complexity lies in the size of the state space, which is mainly defined by the possible values of $\xi _t$. To find the optimal value, $Q_t$ must be evaluated in each possible state within the state space. For problems with many stages, such as long-term asset allocation, this becomes untractable and thus numerical techniques must be implemented to find near-optimal solutions.

At each iteration, the SDDP is applied and approximates problem (1–2), with the following linear programming (LP) model:

For $t=1$:

$$\begin{aligned} z =&\min _{\theta _2,x_1\ge \ \ell _1}\ \ c_1 x_1 + \theta _2 \end{aligned}$$

(3a)

$$\begin{aligned} \text {s.t.}&\quad A_1x_1\ =\ b_1 - B_1 x_{0} \quad \quad (\pi _1) \end{aligned}$$

(3b)

$$\begin{aligned} \theta _2&\ge g_1^{k,s} + {G_1^{k,s}}x_1,\ k=1,\ldots ,K,s=1,\ldots ,N \end{aligned}$$

(3c)

For $t=2,\ldots ,T$:

$$ \begin{gathered} Q_{t} (x_{{t - 1}} ,\xi _{t} ) = \min _{{\theta _{{t + 1}} ,x_{t} \ge \;\ell _{t} }} \;\;c_{t} x_{t} + \theta _{{t + 1}} \hfill \\ {\text{s}}{\text{.t}}{\text{.}}\;A_{t} x_{t} \; = \;b_{t} - B_{t} x_{{t - 1}} \quad \quad (\pi _{t} ) \hfill \\ \end{gathered} $$

(4a)

$$\begin{aligned} \theta _{t+1}&\ge g_{t}^{k,s} + G_{t}^{k,s}x_t,\ k=1,\ldots ,K, s=1,\ldots ,N \end{aligned}$$

(4b)

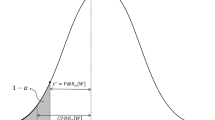
The idea is to evaluate ${\mathbb {E}}[Q_{t+1}(x_{t},\xi _{t+1})]$ with linear approximations (cuts), and thus avoid computing this term in every possible state. These cuts are added into Eqs. (3c–4c), which produces outer approximations of the function, as illustrated in Fig. 2. Coefficients $g_{t}^{k,s}$ and $G_{t}^{k,s}$ are obtained by solving the dual problem. The dual variables are denoted by $\pi _t$ and also depend on $\xi _{t}$.

Fig. 2

Linear approximations (dashed lines) of the exact value of function Q

Based on Philpott and De Matos (2012), a pseudocode is presented below. At each iteration k, we start with the forward pass. In this step, N scenarios are sampled and problems (3–4) are solved sequentially at each period t. Solution ${\bar{x}}_{t-1}^{k,s}$ and function value ${\bar{Q}}_t({\bar{x}}^{k,s}_{t-1},\xi _{t})$ are saved for each scenario s, which is used to solve the problem in the next period. With the forward pass, we can estimate a lower bound $z_l$, which equals the value ${\bar{z}}^k$ obtained in the forward pass process, and an upper bound $z_u$, which is the sample average of the costs, defined by the cuts when applied to the N sampled scenarios. With both bounds, we are able to determine whether we are close to optimality. The pseudo-code shows the standard convergence test, where the gap between the bounds assumes a normal uncertainty in the estimation of $z_u$. The stopping criterion is met if $z_l$ is within the $\alpha$-confidence interval of $z_u$.

The last step is to generate new cuts with the backward pass. For each period t and scenario s, problem (4) is solved for each possible value of $\xi _{t}$, using the stored decisions in the forward pass step from previous period $\bar{x}^{k,s}_{t-1}$. The dual variable $\pi _t$ of equation 4b) is used to define gradient ${\bar{\pi }}_t=E[\pi _t]$, and to generate $N$ new cuts (for each scenario s in period $t{-}1$) by defining $G_{t}^{k,s}=-{\bar{\pi }}_t^{\top } B_t$ and $g_{t}^{k,s}={\bar{Q}}_t({\bar{x}}^{k,s}_{t-1},\xi _{t})$. This procedure is done moving backwards in time.

The curse of dimensionality is not only avoided by approximating the value of ${\mathbb {E}}[Q_{t+1}(x_{t},\xi _{t+1})]$, but also by sampling instead of generating every possible value of the stochastic process. With respect to the efficiency of the SDDP, Shapiro (2011) concludes that, even though convergence is not guaranteed within a reasonable time, the method generally gives high-quality solutions.

The SDDP, as designed initially by Pereira and Pinto (1991), can be applied to value functions Q that are convex for each variable (for minimization problems). Thus, models maximizing the mean utility function, which is concave with respect to asset positions, could be solved using the SDDP method. Furthermore, Downward et al. (2020) develop an extension of SDDP to cope with cases where the value function is concave (for minimization problems) with respect to some variables. This could be the case for economic problems maximizing revenues; stochastic prices are multiplied by quantity variables, making the value function convex in the quantities but concave in the prices. For this type of problems, Downward et al. (2020) implement an idea developed in Baucke et al. (2017) to bound non-convex value functions, which is incorporated into the sddp.jl package.

Based on research such as Philpott et al. (2013) and Shapiro et al. (2013), we can now add risk measures when finding the optimal solution, without needing to use a utility function to handle risk aversion. This consists of replacing the expected value at every stage in (2) by

$$\begin{aligned} \rho [X] = \beta {\mathbb {E}}[X] + (1{-}\beta )\text {RM}[X], \end{aligned}$$

(5)

where $\beta \in [0,1]$, which is a convex combination of the expected value and the risk measure (RM). An example of a risk measure is the Conditional Value-at-Risk (CVaR). CVaR was originally proposed in Rockafellar and Uryasev (2000), and has been extended to a multistage context in several recent publications, e.g. Reus et al. (2019). The $\alpha$-CVaR represents the average of the losses beyond the $\alpha$-quantile, and it controls the tail of the loss distribution. This feature is available in sddp.jl and could be handy for asset allocation problems.

3.2 Asset Allocation Model

The sets to consider are the periods (times) at which the portfolio can be rebalanced, $t {\in } \{1\ldots T\}$, and the available assets with which the portfolio can be constructed, $k {\in } \{1\ldots N\}$. The decision variables are the amount ($) $buy_{k,t}$ ($sell_{k,t}$) of asset k to be bought (sold) in period t. The stochastic process corresponds to

• $\xi _{k,t}$: Price increase (decrease) (%) of asset k in period t

• $\pi _{t}$: Regime (state of the economy) in period t

For details about the distribution of the previous variables, see Sect. 3.4. There are also state (endogenous) variables, which depend on the trades made ($buy_{k,t}$ and $sell_{k,t}$), and the changes in the prices and regimes. These are

• $X_{k,t}$: Position invested ($) in asset k at the end of period t

• $CASH_{t}$: Cash available ($) at the end of period t; corresponds to what is not invested in the assets, and is assumed to be reinvested at a risk-free rate

• $P_{k,t}$: Price of asset k at the end of period t

• $E_{t}$: State of the economy (regime) at the end of period t

The parameters needed are

• $X_{k,0}$ and $CASH_{0,t}$: Initial positions in assets and cash holdings

• $r^{I}_{t}$: Rate of return (goals) defined by the investor in period t. With this return series, we can define the cumulative returns of the index I in period t, which equal $R^{I}_t=R^{I}_0\prod _{k=1}^t (1+r^{I}_{k})$. Note that $R^{I}_t$ is deterministic and that $R^{I}_0$ equals the initial value of the total assets, i.e. $R^{I}_0=\sum _{k=1}^N X_{k,0}+CASH_0$

• $r^f$: Risk-free rate of return

• $c_{k}$: Rebalancing transaction costs, which are a percentage of the amount traded and approximately equal to the bid-ask spread of each asset k

One additional variable, denoted by $dev^{I}_{t} \ge 0$, is introduced to measure the negative deviation between the cumulative returns of the replicating portfolio (including cash holdings) and the synthetic index I.² The cumulative returns are equal to the value of the portfolio including cash holdings, which equals $\sum _{k=1}^N X_{k,t}+CASH_t$

The deviation should take the following values

$$\begin{aligned} dev^{I}_{t}= {\left\{ \begin{array}{ll} 1-\frac{\sum _{k=1}^N X_{k,t} + CASH_t}{R^{I}_t}, &\quad \text {if} \quad \sum _{k=1}^N X_{k,t} + CASH_t \le R^{I}_t \\ 0, &\quad \text {otherwise} \end{array}\right. } \end{aligned}$$

(6)

Defining $\vec {x}_t=[x_{1,t},x_{2,t}\ldots x_{N,t}]$ for any vector depending on the N risky assets, the model can be written as follows

$$\begin{aligned} Q_{t}(\vec {X_{t-1}},CASH_{t-1},\vec {P}_{t-1},E_{t-1},\vec {\xi }_{t},\pi _{t})&=\min \, dev^{I}_{t} \nonumber \\&+ {\mathbb {E}}[Q_{t+1}(\vec {X_{t}},CASH_{t},\vec {P}_{t},E_{t},\vec {\xi }_{t+1},\pi _{t+1})] \end{aligned}$$

(7a)

$$\begin{aligned} \text {subject to:} \quad \quad R^{I}_tdev^{I}_{t}&\ge R^{I}_t -(\sum _{k=1}^N X_{k,t} + CASH_t) \quad \forall t \ge 1 \end{aligned}$$

(7b)

$$\begin{aligned} X_{k,t}&= X_{k,t-1}\xi _{k,t}+buy_{k,t}-sell_{k,t} \quad \forall k, t \ge 1 \end{aligned}$$

(7c)

$$\begin{aligned} CASH_{t} = CASH_{t-1}(1+r^f)-&\sum _{k=1}^N (1+c_{k})buy_{k,t} \nonumber \\&+ \sum _{k=1}^N (1-c_{k})sell_{k,t} \quad \forall k, t \ge 1 \end{aligned}$$

(7d)

$$\begin{aligned} P_{k,t}&= P_{k,t-1}\xi _{k,t} \quad \forall k, t \ge 1 \end{aligned}$$

(7e)

$$\begin{aligned} E_{t}&=\pi _{t} \quad \forall t \ge 1 \end{aligned}$$

(7f)

$$ \overrightarrow {{buy}} _{t} \ge 0,\;\;\overrightarrow {{sell}} _{t} \ge 0,\;\;dev_{t}^{I} {\text{ }} \ge 0,\;\;\vec{X}_{t} \ge 0,\;\;CASH_{t} \ge 0 $$

(7g)

Constraints (7b) define the deviation variable in terms of Eq. (6), whereas the constraints in (7e) and (7f) update the asset prices and regimes according to their respective stochastic processes. We need to track the regime stochastic process with a state variable, because the distributions of the stochastic variables $\vec {\xi }_{t}$ and $\pi _{t}$ depend on the current regime $E_{t-1}$, as seen in Sect. 3.4. Equations (7c and 7d) update the asset and cash holdings based on the realized returns and trades, including transaction costs.

The final value function is 0, that is, $Q_{T+1}(\cdot )=0$. We include the constraint $\vec {X}_t\ge 0$ to ensure there is no short-selling. However, the model could allow short positions within margin constraints if we added $\vec {X}_t\ge -\vec {L}$.

3.3 Auxiliary Indexes

It is possible to add auxiliary indexes with other predefined returns, for better control of the deviations of the portfolio. To illustrate the latter, consider the example in Fig. 3, which shows a 7.5% constant return index and two auxiliary indexes, one with a 10% constant return and another with a 5% constant return. We can measure the deficit in the portfolio value with respect to each index. That is, we can measure $dev^{i}_{t}$ for each index i. In a scenario where cumulative returns are above 10% (Zone A), the chances of going below the 7.5% return index might be low. Thus, in the absence of the 10% return auxiliary index, a risky allocation would be optimal, because there would be nothing to lose. With the auxiliary index, the new goal could be to stay above the 10% return. Thus, the optimal allocation would change to a more conservative one. Analogously, in a scenario with no auxiliary indexes, and where cumulative returns were below 5% (Zone D), the optimal allocation would be a risky one, because that would be the only way to catch the 7.5% return index. However, with the 5% return auxiliary index, the new goal could be to cross the 5% threshold first. Thus, the optimal allocation could be a more conservative one. The allocation differences produced by adding/removing the auxiliary indexes increase when approaching the horizon, because there becomes less time to get things back on track.

Fig. 3

Auxiliary indexes of constant 5% and 10% returns, when cumulative returns are compared to the constant 7.5% return index. Controlling for the performance of the replicating portfolio with respect to the three indexes (Zones A-D) helps to adapt the allocation decisions

Including an auxiliary index in the original model is straightforward. To illustrate how we would add both indexes from the previous example, we denote the auxiliary indexes by $I_{+}$ and $I_{-}$. The objective function (7a) can be written as

$$\begin{aligned} Q_{t}(\cdot ) =\min \ \ \lambda ^{I_{-}}dev^{I_{-}}_t+ \lambda ^I dev^{I}_t + \lambda ^{I_{+}} dev^{I_{+}}_t+ {\mathbb {E}}[Q_{t+1}(\cdot )] \end{aligned}$$

(8)

where $dev^{i}_t$ correspond to the negative deviations with respect to index i. The parameter $\lambda ^{i}$ allows different degrees of penalties to be set for each index. We can denote the user-defined returns of the two auxiliary indexes by $r^{I_{+}}_{t}$ and $r^{I_{-}}_{t}$ and the cumulative returns by $R^{I_{+}}_t$ and $R^{I_{-}}_t$ respectively. Equation (7b) must be added to each index, as follows:

$$\begin{aligned} R^{I_{+}}_tdev^{I_{+}}_t&\ge R^{I_{+}}_t- (\sum _{k=1}^N X_{k,t} + CASH_t)\\ R^{I_{-}}_tdev^{I_{-}}_t&\ge R^{I_{-}}_t- (\sum _{k=1}^N X_{k,t} + CASH_t) \end{aligned}$$

As we will see in the results, we can adjust $\lambda ^{i}$ in Eq. (8) to increase the performance (reduce negative deviation) in worst case scenarios, just as risk measures do.

3.4 Price Model

Not every price model can be represented in the SDDP. The algorithm was first designed to work with random variables that are stage-wise independent, which is not a suitable model for asset allocation problems. Afterwards, new research emerged to include time-dependent processes, such as Infanger and Morton (1996). Shapiro et al. (2013) show how to include autoregressive processes in the SDDP, and Philpott and De Matos (2012) explain how to work with discrete Markov chains. In a recent publication, Löhndorf and Shapiro (2019) show that the optimality gap closes faster with Markov processes than with autoregressive time series. The SDDP Julia package allows both types of process to be employed. However, we cannot handle random processes for which the noise depends on the state of the process. This means, for example, that we cannot include mean-reverting behaviors in asset returns.

In our work, prices follow the structure of a discrete lattice of Ekvall (1996), which applies for multi-asset problems. There are other models that generate lattices for a multi-asset framework, e.g. Boyle et al. (2015) and Moon et al. (2008). However, depending on the data, these methods can produce scenarios with negative probabilities.

Prices satisfy the multi-asset version of a geometric Brownian motion

$$\begin{aligned} dP_{k,t} =\mu _kP_{k,t}dt + \sigma _kP_{k,t}dW_{k,t}, \quad \quad cov(dW_{k,t},dW_{j,t})=\rho _{k,j}dt \end{aligned}$$

with k, j : 1..N. Defining $\Omega$ as the covariance matrix with correlations $\rho$ and volatilities $\sigma$, L as the Cholesky decomposition of $\Omega$ ($\Omega =LL^T$), and $\upsilon =L^{-1}(\mu -\frac{\sigma ^2}{2})$, there are two possible outcomes for each asset k: to move up or down by a factor of $\exp \{\upsilon _k\Delta t{+}\sqrt{\Delta t}\}$ or $\exp \{\upsilon _k\Delta t{-}\sqrt{\Delta t}\}$ respectively. Thus, the price of asset k in the next period can be written as

$$\begin{aligned} P_{k,t+\Delta t} =P_{k,t}\exp \{\upsilon _k\Delta t\pm \sqrt{\Delta t}\} \end{aligned}$$

with jump probabilities that equal $q_s{=}\frac{1}{2^N}$. Figure 4 illustrates how the structure of a lattice substantially reduces the amount of possible states for future prices, compared to a general scenario tree structure. In general, if we have S stages (time periods in our context), the binomial lattice structure produces $\sum _{k=1}^{S} k^N{\le }S^{N+1}$ states from stages 1 to S. This is substantially lower than the amount of states produced in a general scenario tree, which equals to $\sum _{k=0}^{S{-}1} 2^{Nk}{=}\frac{2^{NS}{-}1}{2^N{-}1}$ (and approximately $2^{(S{-}1)N}$ for higher values of N). Note that the dimension of the lattice still growths exponentially with the amount of assets.

We assume that the states of the economy (e) follow a discrete Markov process, where $M_{e,e'}$ is the transition of going from regime (economy) e to regime $e'$. Recall that $\pi _t$ denotes the random variable of the economy at period t, which depends on current state $E_{t-1}$. The relationship is the following: if $E_{t-1}=e$, then $P(\pi _t=e')=M_{e,e'}$.

For each state, we calibrate parameter $(\upsilon ^e)$ and compute the two possible outcomes with $\exp \{\upsilon ^{e}_k\Delta t\pm \sqrt{\Delta t}\}$. The transition probability $q_{(s,e)}^{(s',e')}$ of going from scenario s in regime e to scenario $s'$ in regime $e'$ equals $q_{(s,e)}^{(s',e')}=M_{e,e'}\frac{1}{2^N}$.

Fig. 4

Scenario structure for price movements when $N{=}1$ and $S{=}5$. (Left): General scenario tree. The number of states (nodes) is equal to $\frac{2^5{-}1}{2{-}1}{=}31$. (Right): Lattice. The number of states (nodes) is equal to $\sum _{k=1}^{5} k{=}15$

3.5 Benchmark and Performance Measures

The results of our model are compared to those of a strategy based on the mean-variance solution (Markowitz). There will be one portfolio for each state of the economy. Each portfolio is derived by solving the mean-variance problem with the data from that particular regime, and including the transition probabilities of going to other regimes. The benchmark consists of holding the corresponding portfolio of the current regime. Thus, the benchmark is rebalanced only when there is a change in the state of the economy.

To be more precise, suppose that we have the data of the expected returns $\mu _{i}$ and covariance matrix $\Sigma _{i}$ at each regime i. We want to compute the expected returns ${\hat{\mu }}_e$ and covariance matrix ${\hat{\Sigma }}_e$ of current regime e for the next period, that is, considering the transition probabilities. With ${\hat{\mu }}_e$ and ${\hat{\Sigma }}_e$, we are able to build the portfolio with the mean-variance solution. Denoting E as the number of states in the economy, it is not hard to see that

$$\begin{aligned} \hat{\mu}_e =\sum_{i=1} ^E \mu_i M_{e,i}, \quad \quad \hat{\Sigma}_e = \sum_{i=1}^E (\Sigma_i+\mu_i\mu_i^T) M_{e,i} -\hat{\mu} _e\hat{\mu}_e^T \end{aligned}$$

It can be argued that a benchmark based on the mean-variance approach is too naive. As seen in Best and Grauer (1991), or more recently Bessler et al. (2017), the mean-variance solution suffers from being sensitive to parameter estimation. Thus, it can lead to poor performance when the out-of-sample distribution of assets’ prices differs from the in-sample distribution. In our experiments, however, this will not be the case since simulations to measure the performance of both strategies (SDDP and the benchmark) will be generated with the same distribution as the one used in the allocation process.³ The parameters used to generate future prices will not change within the evaluation period either. In other words, realized returns from time 0 to the current period will not change the distribution of the pricing model in either regime. Thus, if there is no change in regime in the current period, there will be no need to rebalance the benchmark portfolio, because it will remain optimal in terms of mean-variance compromise. Hence the mean-variance is a competitive solution under this setting.

The reason we simulate in this way is not for simplification purposes, but rather to make a fair comparison when evaluating the performance of the SDDP and the benchmark solutions. Under this setting, any potential difference in performance can only be caused by allocation decisions and cannot be attributed to sample or estimation bias.

The performance of each solution is measured by the following metrics.

• 1. Returns (R), defined as $(1{+}R)^T=\frac{\sum _{k=1}^N X_{k,T} {+} CASH_T}{\sum _{k=1}^N X_{k,0} {+} CASH_0}$

• 2. Semi-tracking error (STE): Tracks the negative deviations of the cumulative returns of the replicating portfolio with respect to the index, and is equal to

  $$\begin{aligned} STE=\sqrt{\frac{1}{T}\sum _{t=1}^T \max \{0,\frac{R^{I}_t}{\sum _{k=1}^N X_{k,t} {+} CASH_t}{-}1\}^2} \end{aligned}$$

The evaluation of a solution consists of estimating the previous measures in each simulation. Thus, the comparison between the SDDP and the benchmark is based on six statistics derived from those simulations: mean, standard deviation, Value-at-Risk (VaR), CVaR, skewness and kurtosis. For the returns R, VaR and CVaR are measured at the $10^{th}$ percentile, because we want to control the returns in the worst-case scenarios (left tail). On the contrary, the VaR and CVaR of the STE are measured at the $90^{th}$ percentile, because the worst-case scenarios are in the right tail for them.

4 Results

4.1 Data

We test the proposed methodology in a seven-year and quarterly rebalancing problem, which, in terms of dimensionality, equates to a 28-year problem with annual rebalancing. The reason for choosing the first setting is that we want transaction costs to come into play. With annual rebalancing, these costs are not relevant, even with high turnover rates.

We want to illustrate how the model performs when dealing with strategic allocation to different asset classes. For that purpose, we choose a pool of $N{=}6$ different exchange traded funds (ETFs), each one tracking an index of one asset class, and thus representing that asset class. The model does not aim to track the ETF or the underlying index of the ETF, but rather uses the ETFs as assets to track the synthetic index. Note that approximately 2180 million ($2^{31}$) states are produced by the lattice structure when dealing with 6 assets and 28 time periods (see Sect. 3.4).

Table 1 shows the annualized average returns, volatilities and correlations of the ETF monthly returns, in two sets of data. The first set corresponds to the behavior of the ETF in a normal state of the economy, according to data taken from the Federal Reserve Economic Data (FRED).⁴ The other set of results is based on data for a recession period. Data are taken from Jan-2006 to Oct-2020. Thus, we include the recessions caused by the subprime crisis (Q1-2008 to Q2-2009) and covid-19 (Q1-2020 to Q3-2020).

In the healthy state of the economy, equity ETFs such as SPY and IJR exhibit the best return-volatility ratio, while bonds (IEF, LQD) offer low-profit and low-risk performance. In the recession periods, gold (GLD), bonds (IEF, TLT, LQD) are the ones showing increases in value. As expected, equity ETFs have low correlation with gold and bond ETFs in both regimes, which produces potential diversification gains. In general terms, funds offer higher correlation among them in the recession period, which is also expected. By looking at the skewness and kurtosis of the ETFs, we can see that the returns are distributed similarly to a normal distribution in most cases. Tests show that we cannot reject normality at 5% for any ETF, except TLT (only in a normal economy) and LQD (only in a recession).⁵ These results are aligned with the GBM model chosen in Sect. 3.4, which implies normally distributed returns.

As a remark, other ETFs representing different asset classes were considered prior to the final selection. Specifically, developed market equities (EFA), emerging market equities (EEM), US real estate (VNQ), inflation-protected securities (TIP), commodities index (GSCI), and private equities (PSP). However, all of these assets under-performed some of the chosen ETFs at every regime. Exploratory results confirmed no allocations were assigned to these discarded assets.

We set $r^f=0.6\%$, which is the average rate seen for the 3-Month US Treasury Bill during the periods Q1-2008 to Q3-2020. Finally, Table 2 shows the dynamics of the states of the economy. Estimations are based on the NBER recession indicators available in FRED, from Q1-1900 to Q3-2020 and on a quarterly basis. The results show the persistence of both states, especially of the healthy economy. Thus, it is expected that we would see a healthy economy in most quarters within the 28 quarters evaluation period, combined with some consecutive quarters of recession.

Table 1 Statistics and correlations of 6 ETFs’ monthly returns. US equities (SPY), US small-cap (IJR), high-grade corporate bonds (LQD), long-term treasury bonds (TLT), medium-term treasury bonds (IEF), gold (GLD)

Table 2 Transition matrix of states of the economy (normal and recession) in in each quarter, and the probability of being in each state

The values for the rest of the parameters are

• Initial values: $CASH_0{=}\$ 100$,    $X_{k,0}{=}0$ $\forall \, k$,    $P_{k,0}{=}\$ 1$ $\forall \, k$

• Trading costs of 25 basis points ($c_{k}{=}0.25\%$).

• Five auxiliary indexes, named $I_{++},I_{+},I,I_{-},I_{--}$ respectively, having constant returns of $r^{I_{++}}_t{=}13\%, r^{I_{+}}_t{=}11\%, r^{I}_t{=}9\%, r^{I_{-}}_t{=}7\%, r^{I_{--}}_t{=}5\%$, respectively.

• Under a normal economy, the benchmark expected return is set to 10% and in recession years, the expected return is set to 6%. Given the probabilities of being in each state, this implies an expected return of 9%, which equals the predefined return of the synthetic index $r^{I}_t$.

The model is implemented using the sddp.jl package in Julia (see Dowson and Kapelevich (2017) for details). The package allows us to program the model without needing to deal with the implementation of the SDDP algorithm. The solution of the model can be obtained through an in-built sampling procedure that can be used to derive the allocation policy. After some calibration, it was found that 10,000 scenarios were enough to achieve a representative sample of future prices. The LP solver used within the SDDP procedure is Gurobi and the experiments were done in a MacBook Pro with a 2 GHz Quad-Core Intel Core i5 processor and a 16 GB ram memory. The CPU time taken to reach a solution (like the ones seen on Tables 3 and 4) was less than two hours.

4.2 Performance

The results in Table 3 show that, on average, the solution of the SDDP achieves the predefined 9% target. It outperforms the benchmark solution in terms of average returns (9.1% vs. 8.9%) and volatility (3.6% vs. 4.4%). The CVaR, which measures the mean of the worst 1,000 scenarios, is equal to 1.4% in both solutions. However, the VaR obtained by the SDDP is significantly better (4.0% vs. 3.3%).⁶

As expected, the SDDP presents a better tracking performance. It reduces the average STE of the benchmark by approximately 13% (18.2% to 15.8%) and also reduces the tracking error in the worst-case scenarios. Although the CVaR is similar in both solutions, the VaR with the SDDP is reduced by 9% (44.8% to 40.7%). The skewness and kurtosis of the positive variable STE is higher in the SDDP solution. This means that the number of scenarios with no (or low) negative deviations, relative to the number of cases with huge negative deviations, is greater in the SDDP solution than in the benchmark solution.

Figure 5 also shows the performance differences seen in Table 3. It illustrates the influence of the indexes in the SDDP solution. The portfolio generated by the SDDP solution aims to track the cumulative returns of the nearest index. In contrast, the cumulative returns of the benchmark solution have more of a random-walk pattern. In fact, the returns of the benchmark are closer to being normally distributed, which is aligned with the absence of skewness and excess kurtosis seen in Table 3.

Table 3 Model and benchmark performance

Fig. 5

Cumulative returns of a random sample of 500 scenarios: Model (Left), Benchmark (Right). Showing only a set of paths serves better for illustration purposes. The analysis also holds for other samples of scenarios

Table 4 shows the performance of the SDDP solution under changes in $\beta$ of Eq. (5) or the deviation penalties $\lambda ^{i}$. Each column denotes the results obtained for a particular configuration, with the solutions labeled M0 and B of Table 3. The benefit of using auxiliary variables can be seen when comparing the performance of M2 with M4, which has no auxiliary indexes. Solutions M1 and M2 exemplify how we can derive solutions with different return-risk profiles by changing the weight $\beta$ assigned to the risk measure in the objective function. In the case of solution M1 (M2), the risk aversion is higher(lower) than M0, and thus we get better(worse) performance on average, but worse(better) results in worst case scenarios. The effect produced by a reduction in $\beta$ like in M1 can also be achieved by adding more weight to the auxiliary indexes with lower targets returns, as seen in M3. M3 has better performance than M1, but M3 needed a change in five parameters, instead of M1 that needed a change in only one parameter.

Table 4 Performance with different settings. (M1): $\beta {=}0.8$ and same weights for $\lambda ^{i}$. (M2): $\beta {=}1.0$ and same weights for $\lambda ^{i}$. (M3): $\beta {=}1.0$ and $\lambda ^{I_{++}}{=}1$, $\lambda ^{I_{+}}{=}7.5$, $\lambda ^{I}{=}15$, $\lambda ^{I_{-}}{=}25$, $\lambda ^{I_{--}}{=}50$. (M4): $\beta {=}1.0$ and no auxiliary indexes. (*): VaR and CVaR are measured at the $10^{th}$ percentile for R and at $90^{th}$ percentile for STE

4.3 Allocations

The benchmark portfolio is displayed in Fig. 6. In a normal economy, the benchmark chooses to invest heavily in equity (SPY and IJR) and gold (GLD). In recession periods, the benchmark chooses to leave 33% in cash, and distribute among more conservative assets like medium-term treasury bonds (IEF) and gold. Only a small amount is allocated in high-grade corporate bonds (LQD).

Fig. 6

Benchmark solution for normal and recession states of the economy. Expected returns are set to 10% in normal periods and 6% in recession periods

The dynamic allocation of the SDDP model is shown in Fig. 7. The composition of the portfolio changes depending on the current cumulative return and the proximity to the horizon. Given the high probability of staying in the current regime, the composition also changes in each state of the economy. In a normal economy, for example, positions in equity could be even higher than in the benchmark solution, especially when the replicating portfolio is way below the original target (e.g. the below 5% case). In those cases, the SDDP increases the allocations in the small-cap IJR. When the results are better with respect to the 9% target, the policy diversifies into more conservative and low-correlated assets, such as long-term sovereign bonds (which is not used by the benchmark) and gold. Moreover, it uses cash as a refuge when the results are way above the goal (e.g. the over 13% case). This transition accentuates as we approach the horizon, as there becomes less time available for possible recoveries. In recession periods, the SDDP policy invests heavily in gold. This is especially the case when the results are below the goal, because GLD is the asset with the highest returns in this state. When cumulative returns are higher, the SDDP policy gradually diversifies into all types of bonds (TLT, IEF and LQD) and into cash.

Note that the assets used by the SDDP are almost the same as the ones employed by the benchmark solution, in both states of the economy. The difference comes in the composition. On average, the SDDP allocates more to GLD and TLT. Both assets perform well in both states. Thus, it is sensible to consider both in the case that there is a change in regime and also for reducing turnover.

A good feature of the SDDP solution is its stability. That is, changes in portfolio composition are small when maintaining the same performance as in previous periods. The allocation does not change drastically between two portfolios with a small performance difference in a specific time period. Thus, it reduces the complexity of defining and implementing allocation policies.

Fig. 7

Dynamic allocation policy derived from the SDDP solution, depending on cumulative returns. For example, the plot titled “Above 13%” corresponds to scenarios where the replicating portfolio is above the 13% auxiliary index. (Upper half): Policy under normal economy, (Lower half): Policy under recession. Note that decisions shown at quarter t are based on the deviations found by the end of previous quarter $t{-}1$. Allocation at $t{=}1$ is not shown because there are no realizations before that allocation

5 Conclusion

We have presented a new application of the SDDP to an asset allocation problem, with the particular goal of achieving predefined returns over time. To do this, we model an index-tracking problem, where the index includes the investor’s goals in terms of profits. Since the SDDP handles large-scale multistage stochastic problems, it enables us to find dynamic allocation policies for either long-term applications, as in the case of pension funds, or short-term applications with more intensive portfolio rebalancing.

Using ETF market data, our numerical experiments show how the methodology delivers allocations with better performance, in terms of both returns and tracking measures, when compared with the mean-variance allocation. The SDDP provides sensible allocations that change depending on how the replicating portfolio performs with respect to the index, the state of the economy, and also with the proximity to the investment horizon.

Note that experiments were conducted to illustrate how this quantitative tool could provide smart and intuitive allocations, rather than to solve a real case study. The reason for implementing this tool is not based on finding possible optimal, but counter-intuitive allocations. It consists of defining an intuitive and strategic allocation policy, based on a quantitative and systematic procedure, which determines the right amount of over(under)weighting of each asset under different scenarios. Moreover, the methodology can serve to help us understand the settings under which a dynamic policy is needed for better performance and when it is not.

One possible extension to this work would be to include a more sophisticated price model. For example, one could include a dynamic volatility and drifts to generate future prices, that could change the distribution of returns over time. In such a way, the tool would be more robust for use in real-world applications. Another possibility would be to explore the use of a dynamic index, that is, an index that endogenously changes its user-defined return depending on the portfolio performance over time. This could eventually replace the use of auxiliary variables. However, in that case, constraint (7b) would be non-linear, because the cumulative return on the index would also be endogenous, and thus the problem would be more complex to solve.