Introduction

The recent experimental realization of two-dimensional (2D) magnetic crystals like CrI31,2,3, CrGeTe34, and VSe25, has sparked great interest for possible applications like spintronics6,7, valleytronics8, and skyrmion9-based magnetic memories10,11. However, magnetic order in 2D magnetic crystals is hampered because of low magnetic anisotropy and weak exchange interaction strength12, resulting in low Curie temperatures (e.g., 45 K for CrI3 and 42 K for CrGeTe3), which limits their use in commercial applications.

Semiconducting 2D materials doped with impurity atoms, e.g., doped graphene13 and metal-doped transition-metal dichalcogenides (TMDs)14,15,16,17,18, have emerged as promising candidates for high-temperature 2D magnetic order. Semiconductors doped with transition metal impurities couple the properties of semiconductors and magnets and are called dilute magnetic semiconductors (DMS). The ability to control magnetic order through charge transfer in a DMS19,20,21 opens up the possibility for realizing magnetic devices because their magnetic state can be controlled using an external electric field22.

Among semiconducting 2D materials, which can be used as a base material for 2D DMSs, TMDs are of special interest. The heavy atomic mass of TMDs can lead to larger magnetic anisotropy, which is necessary for the existence of magnetic order in 2D23. The interest in TMDs is further fueled by recent experimental results that have demonstrated the existence of stable magnetic order in TMDs doped with a transition metal impurity24,25,26.

For the technological application of magnetically doped TMDs, it is necessary to find the optimal combination of a TMD and a dopant. However, the number of possible TMDs and dopant combinations is too large for a comprehensive experimental investigation, and theoretical guidance is desired. There have been previous theoretical attempts at modeling doped TMDs and calculating their critical temperature14,15,16,27. However, previous theoretical predictions of the Curie temperature of doped TMDs have predicted unrealistically high Curie temperatures in excess of 1000 K at low doping concentrations (≈5%)14,15,16,27, whereas experimental observations to date suggest a Curie temperature below 350 K at such doping levels24,25,28,29.

The reason for the discrepancy between the experimental and the theoretical work is that previous theoretical works have ignored the effect of magnetic anisotropy30 and have used the collinear magnetic approximation31. Most of the previous theoretical works have either calculated the Curie temperature using the Ising model15, or the mean-field approximation14. Unfortunately, both methods (Ising and mean-field) result in an overestimation of the actual Curie temperature32. Moreover, previous theoretical works have taken into account only a few combinations of dopants and TMDs, and a comprehensive study for a vast set of TMDs doped with period four transition metals is still missing.

In this work, we calculate the critical temperature (Curie temperature or Kosterlitz-Thouless (K–T) transition temperature) for a set of 2H TMDs: MoS2, MoSe2, WSe2, WS2, and MoTe2, substitutionally doped with all the period four transition metals starting from Ti to Ni (Ti, V, Cr, Mn, Fe, Co, Ni). To model the magnetic structure of doped TMDs, we use our method, developed in ref. 12. We model the magnetic exchange interaction (J) using a parametrized functional form (J(r)) and fit its parameters to first-principles calculations. Finally, we calculate the concentration-dependent critical temperature using the Monte-Carlo method. First, we apply our method to one of the TMDs, MoSe2, doped with all period four transition metals, and show all the possible magnetic ordered states originating from different dopants. Next, we present the magnetically ordered states and the critical temperature for all the TMDs doped with period four transition metals. We find that out of the thirty-five material combinations investigated, ten are non-magnetic (NM), nine are anti-ferromagnetic (AFM), and sixteen are ferromagnetic (FM). Out of the 16 FMs, 6 are FMs with an in-plane magnetic easy-axis, and the other 10 have an out-of-plane easy-axis. We find that the most promising FMs can be realized by doping MoSe2 and WSe2 with V along with doping MoS2 with Mn, which have a Curie temperature of approximately 200 K at an atomic substitution of 15%.

Results

Computational model

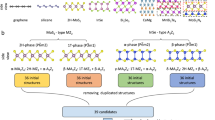
 Figure 1 illustrates our computational model, which has two parts: DFT and Spin-Model. To reduce the computational cost and weed out the candidate ferromagnets, in the first part (DFT), we determine the magnetic ground state of the doped TMD by substituting the transition metal with two dopants in a supercell of size 3 × 3 × 1. If out of all possible magnetic configurations, the ferromagnetic state has the lowest energy, we make bigger supercells (4 × 4 × 1, 5 × 5 × 1, and 7 × 7 × 1) of the corresponding TMD and dopant. We substitute two transition-metal atoms (W/Mo) in the TMD supercells with dopant atoms separated at distances ranging from the nearest neighbor to the fifth neighbor. We calculate the total energy for both the FM and the AFM magnetic orders with both the in-plane and the out-of-plane magnetic easy axis for the bigger supercells of TMDs12.

Fig. 1: Computational model for calculating the critical temperature.
figure 1

Different blocks show the different steps for calculating the critical temperature in substitutionally doped TMDs, combining DFT and the spin-model.

Full size image

In the second part (Spin-model), we model the magnetic structure of doped TMDs using a classical Heisenberg Hamiltonian, which features parameterized exchange tensor Ji,j, and onsite anisotropy D determined from DFT12. Specifically, we approximate the elements of Ji,j tensor as a continuous function of distance J(ri − rj) (see Eq. (2) in the Methodology section). We go beyond the nearest-neighbor interaction because long-range interaction plays a decisive role in determining the magnetically ordered state of doped materials33,34. We take into account the exchange interactions up to the 5th neighbor (N = 5), beyond the 5th nearest neighbor the exchange interaction (J(r)) is numerically truncated.

To obtain the parameters for J(r), we fit the parameterized Heisenberg Hamiltonian to the total energy obtained in the DFT step. The details of our fitting procedure are outlined in ref. 12. We study the phase change of the parameterized Heisenberg Hamiltonian for large (40 × 40) supercells with an atomic substitution ranging from 6% to 18%, using the Monte-Carlo (MC) algorithm. We obtain the median critical temperature (Curie/K–T) from the peak of the average susceptibility for each percent atomic substitution, obtained from the MC simulations. For each percent substitution, we average over 20 different substitutional configurations to account for configurational entropy. We provide further computational details and parameters at the end of this article.

Magnetic order in MoSe2

We first apply our computational method to MoSe2 doped with all period four transition metals. We present all possible magnetically ordered states in doped MoSe2: the non-magnetic state (NM), the ferromagnetic state with out-of-plane spin polarization (Z FM), the out-of-plane polarized clustered FMs (clustered Z FM), the in-plane polarized FMs (X–Y FM), and the anti-ferromagnetic state (AFM). We then apply our method to all the TMDs doped with period four transition metals and calculate their critical temperature and uncover their magnetically ordered phase at the atomic substitution of 15%.

We perform DFT calculations on a 3 × 3 × 1 cell of MoSe2 doped with two dopant atoms (Ti, V, Mn, Cr, Fe, Co, Ni), which amounts to 22.22% atomic substitution. We define the atomic substitution using, \(\frac{{N}_{{\rm{dopant}}}}{{N}_{{\rm{transition-metal}}}}\), where Ndopant is the number of dopant atoms and Ntransition-metal is the total number of transition metal atoms in the TMD supercell. We find that Ni and Ti as dopants result in a negligible magnetic moment of 0.09 μB per dopant. Hence, Ni and Ti as dopants result in a weakly-magnetic/non-magnetic (NM) state in MoSe2. On the other hand, V, Cr, Mn, Fe, and Co have a magnetic moment of 1.7 μB, 3.0 μB, 3.7 μB, 3.1 μB, and 1.6 μB per dopant, respectively. We find that the magnetic easy-axis is in-plane for Fe and Mn, whereas it is out-of-plane for V and Co-doped MoSe2.

 Figure 2a shows the concentration-dependent critical temperature (Curie temperature for out-of-plane FM and Kosterlitz-Thouless transition temperature for in-plane FM) of MoSe2 doped with V, Mn, Fe, and Co. We observe that V-doped MoSe2 exhibits room-temperature out-of-plane FM at an atomic substitution of about 16.5%, and Fe-doped MoSe2 exhibits room-temperature in-plane FM at an atomic substitution of 16%. We also observe that the variance in the obtained critical temperatures is very low across different substitutional configurations (<30 K) except for Co doping. Low variance implies that the critical temperature is robust to the random position of dopants in V, Fe, and Mn-doped MoSe2.

Fig. 2: Critical temperature and magnetization of doped MoSe2.
figure 2

a Critical temperature (Curie temperature for V and Co and K-T transition temperature for Fe and Mn) of V, Mn, Fe, and Co-doped MoSe2 as a function of atomic substitution. The solid lines show the median critical temperature obtained from the MC simulations, and the shading shows the variance between the 25th and the 75th percentile. b The average magnetization of V, Mn, Fe, and Co-doped MoSe2 as a function of atomic substitution. The solid lines show the median magnetization obtained from the MC simulations, and the shading shows the variance between the 25th and the 75th percentile. The dotted lines show the starting saturation magnetization for each dopant, obtained from DFT.

Full size image

 Figure 2b shows the saturation magnetization (M = √(Sx2 + Sy2 + Sz2)) per dopant atom in V, Mn, Fe, and Co-doped MoSe2, obtained from the MC simulations at an atomic substitution ranging from 6% to 18%. The dotted lines show the starting magnetization of each magnetic dopant at the start of the MC simulation (also shown in Table 1). We observe that the saturation magnetization in V-doped MoSe2 remains almost flat, and decreases slightly at a percent substitution below 7%. For Fe, the saturation magnetization increases with increasing atomic substitution and saturates to its maximum magnetization at around 18% atomic substitution. However, for both Mn and Co-doped MoSe2, the saturation magnetization remains far below their respective maximum magnetization.

Table 1 Starting magnetic moments.
Full size table

 Figure 3a shows the magnetically ordered state in a sample of V, Cr, and Co-doped MoSe2 at an atomic substitution of 15%, at a temperature of 5 K. We plot the magnetization in the out-of-plane direction \(({\hat{S}}_{{\rm{z}}}={S}_{{\rm{z}}}/| S| )\). The magnetically ordered state in V and Co-doped MoSe2 is FM with an out-of-plane easy axis, whereas, for Cr substitution, the magnetically ordered state is AFM. We observe that the magnetically ordered state of V-doped MoSe2 saturates to a perfect FM state with an out-of-plane easy-axis. For Co dopants, we find that there are clusters of FM-oriented Co ions, but the long-range order is missing. In the case of Cr, we observe that the magnetically ordered state has a randomized magnetic order with spins orienting randomly. The reason for such a randomized magnetically ordered state is that the AFM order leads to a magnetic frustration for some clusters, which leads to a randomized orientation for the magnetic moments.

Fig. 3: Possible magnetically ordered states in doped MoSe2.
figure 3

a The magnetically ordered state of a V, Cr, and Co-doped sample of MoSe2 at an atomic substitution of 15%, at a temperature of 5 K. b The magnetically ordered state of an Mn, Fe-doped sample of MoSe2 at an atomic substitution of 15%, at a temperature of 5 K. ϕ is the in-plane angle of the magnetic moment. Their magnetization as a function of temperature is shown in the supplementary document (Supplementary Fig. 2).

Full size image

 Figure 3b shows the magnetically ordered state in a sample of Fe and Mn-doped MoSe2 at an atomic substitution of 15% at a temperature of 5 K. Because the magnetic easy-axis is in-plane, we plot the in-plane angle (ϕ) of each dopant atom: \(\phi ={\cos }^{-1}({S}_{{\rm{x}}}/| {S}_{\parallel }| )\), where, S∥ is the in-plane magnetization. We observe that for both Mn and Fe, the orientation of the magnetic moment remains randomized with some short-range (<8 Å) order. For both Fe and Mn, we observe two effects. First, we observe domain formation with FM clusters. Second, the FM clusters are not perfectly ferromagnetic because their magnetic order breaks at slightly longer distances. We will discuss domain formation separately later in this section. The slight breaking of magnetic order at a longer distance appears due to the Kosterlitz-Thouless transition behavior35, where, even at temperatures below the K-T transition temperature, long-range magnetic order does not exist.

Interestingly, we see some level of quasi vortex formation both for Fe and Mn-doped MoSe2. The observation is in line with the K–T physics for magnets with in-plane anisotropy35. However, due to broken translational symmetry because of the random placement of defects, as well as finite in-plane anisotropy, vortex formation is imperfect. Nevertheless, observation of quasi vortices in doped MoSe2 implies that the topological vortices in the K–T transition are quite robust to lattice imperfections. However, an in-depth analysis of this phenomenon is beyond the scope of this article.

 Figure 4 shows the exchange function J(r) for doped MoSe2. The solid line shows the average between the exchange between electrons with moments along the x and z-direction (J(r) = (Jx(r) + Jz(r))/2), and the dots show the calculated discrete J parameters obtained from the DFT calculations using the J1 − J2 model31. We define a distance >7 Å as long-range, and <7 Å as short-range (up to the third-nearest neighbor).

Fig. 4: The J(r) for V, Cr, Mn, Fe, and Co-doped MoSe2.
figure 4

Here, J(r) = (Jxx(r) + Jzz(r))/2. The dots show the discrete J parameters calculated using the J1 − J2 model31 and are only meant to illustrate the distances at which the dopants were added for the DFT calculations, and were not used to model the magnetic phase transitions. We zoom the X-axis between 8 Å to 18 Å to show the long-range interaction in the inset.

Full size image

We observe that J(r) is the strongest for V, Fe, and Co-doped MoSe2 in the short range. For Mn, J(r) is weaker in the short range. Whereas, for Cr, J(r < 7 Å) is negative, signifying an AFM interaction. Looking at the long-range interaction beyond 8 Å (inset of Fig. 4), we find that the long-range interaction is strongest in V-doped MoSe2 and significantly weaker in Co and Mn-doped MoSe2. In Fe-doped MoSe2, the long-range interaction is the second highest.

Analyzing the ordered magnetic states for each dopant shown in Fig. 3a and b, their saturation magnetization in Fig. 2b, and their J(r), we find that a strong short-range interaction results in FM cluster formation, e.g., in Co, Fe, and Mn-doped MoSe2, and the clusters then orient randomly due to weak long-range inter-cluster interaction. At higher percent atomic substitution in Fe-doped MoSe2, we find that bigger clusters start forming as seen by the increase in saturation magnetization for Fe-doped MoSe2 at higher atomic substitution, as shown in Fig. 2b. However, the X–Y nature of magnetism prohibits the long-range order in Fe-doped MoSe2. It should also be noted that the appearance of a saturation magnetization at these concentrations in the X–Y magnets is due to the finite size of the lattice, the random position of the magnetic ions, and the long-range behavior of J(r).

To summarize this section, we find that five magnetically ordered states are possible, depending on the J(r) in a doped TMD including,

  1. 1.

    The non-magnetic state (Ti and Ni-doped MoSe2).

  2. 2.

    The frustrated AFM ordered state (Cr-doped MoSe2).

  3. 3.

    The Z FM ordered state with strong long-range interactions, where we observe full FM orientation with their magnetic easy-axis in the out-of-plane direction (V-doped MoSe2).

  4. 4.

    The clustered Z FM ordered state with strong short-range and weak long-range interactions, where we observe weakly interacting clusters of FMs (Co-doped MoSe2).

  5. 5.

    The X–Y ordered state, where we observe weakly aligned in-plane FM clusters, but the long-range order remains significantly randomized at any finite temperature (Mn and Fe-doped MoSe2).

Critical temperature of MoS2, WS2, MoSe2, WSe2, and MoTe2

 Figure 5 shows the magnetically ordered state, as well as the critical temperature at an atomic substitution of 15% for the selected combination of the TMD and the dopant. Material combinations indicated with "Z" are ferromagnetic (FM) with their magnetic easy-axis in the out-of-plane direction, while "X–Y" indicates the X–Y magnets, with an in-plane easy axis. The TMD dopant combinations, which are shaded, are clustered Z FM. Materials indicated as AFM have an anti-ferromagnetic (AFM) ordered state, while (NM) represents a non-magnetic (paramagnetic) state. As discussed above, FMs with an out-of-plane magnetic easy axis have a Curie temperature, while, FMs with an in-plane magnetic axis have a Kosterlitz-Thouless phase transition, which results in a quasi-ordered magnetic state, but the long-range order remains randomized. We provide the full atomic substitution-dependent (6% to 18%) critical temperature for all the Z and the X–Y ferromagnets in the supplementary documentation (Supplementary Table. 2).

Fig. 5: Critical temperature (green for Curie and yellow for K–T) of TMDs at an atomic substitution of 15%.
figure 5

Shaded blocks show out-of-plane FMs with weak long-range interaction leading to clustered FM configurations.

Full size image

Some general trends can be extracted from Fig. 5. We observe that Cr dopants result in an AFM-ordered state for all the TMDs. Ti and Ni as dopants result in a non-magnetic state. Interestingly, V, Fe, and Mn always result in an FM ordered state for all the TMDs except for MoTe2, for which only Fe and Co result in an FM state. Co dopants result in an AFM ordered state for disulfides (MoS2, WS2), but they result in an FM ordered state for diselenides (MoSe2, WSe2), and MoTe2. V dopants always yield an out-of-plane FM. Whereas, Mn and Fe substitution result in an X–Y magnetic order for WS2, MoSe2, and WSe2.

The main highlights of Fig. 5 are the material combinations that result in an out-of-plane FM with strong long-range interaction. We find five combinations with V as a dopant for all the TMDs except MoTe2 and Mn-doped MoS2. Mn substitution in MoS2 results in an FM-ordered state, with high median Curie temperature of 190 K at 15% atomic substitution. Also, V as a dopant in MoSe2 and WSe2 results in an out-of-plane FM with a high Curie temperature measuring ≈200 K.

Finally, we would like to mention that the electronic origin of magnetism in doped TMDs is a result of the super-exchange interaction in the short-range14,16 and carrier-mediated interaction in the long range. For example, the electronic origin of magnetism and the doping stability in MoSe2 are briefly discussed in the supplementary document (Supplementary Fig. 4).

Discussion

We have presented the magnetic order in TMDs doped with period four transition metals. We have determined the nature of the magnetically ordered states, as well as their critical temperature as a function of percent atomic substitution. We showed that there are five possible magnetically ordered states for doped TMDs, depending on the nature of their exchange interaction J(r), the magnetic anisotropy, and the atomic substitution. The possible magnetically ordered states are non-magnetic (NM), perfectly ferromagnetic (FM Z), clustered ferromagnetic (clustered FM Z), X–Y ferromagnetic (X–Y FM), and randomized anti-ferromagnetic (AFM).

We have shown that Ti and Ni dopants always result in a non-magnetic state. Moreover, Cr dopants result in an AFM configuration for all the TMDs. Both Mn and Fe dopants result in an X–Y magnet for MoSe2, WS2, and WSe2. From this study, we conclude that the best chance of realizing a 2D DMS using TMDs with room-temperature Curie temperature is found in Mn-doped MoS2 and V-doped MoSe2 and WSe2 at an atomic substitution in excess of 16.5%.

We have provided a generalized method of modeling the magnetic interaction in doped 2D materials. For further usability of our method, the parameters of the functional form for all the TMD and dopant combinations are provided in a supplementary document (Supplementary Table 1).

There have been recent experimental reports regarding magnetic order in TMDs24,25,26, and FM clusters have been detected in V-doped WSe2, using magnetic scanning tunnel microscopy (MTM)26. The magnetically ordered states presented in this work for transition-metal doped TMDs, and their critical temperature can be verified experimentally using a similar procedure as used in26. Moreover, recent experimental reports have shown that the transition-metal substitution is often accompanied by vacancies36,37, and a possible future extension of our work will be to include the impact of structural defects on the magnetic order of TMDs.

Methods

Magnetic structure and the exchange interactions

We model the magnetic structure of doped TMDs using a parameterized Heisenberg Hamiltonian assuming a localized nature of the magnetic interaction38,

$$H=-\mathop{\sum }\limits_{i,j}{{\bf{S}}}_{i}{J}_{i,j}{{\bf{S}}}_{j}+D\mathop{\sum }\limits_{i}{({{S}}_{i}^{z})}^{2}.$$
(1)

The first term is the exchange term between the ith and the jth magnetic atom (dopant) with S = Sxx + Syy + Szz, as the magnetic moment vector. Ji,j is the strength of the exchange interaction between the ith and the jth magnetic atoms and is a tensor as described in ref. 12. Because anisotropy plays an important role in determining the magnetic ground state of doped magnetic systems39, we take into account the Ji,j tensor instead of an effective isotropic exchange. The second term is the onsite-anisotropy with strength D. We only use the diagonal elements of Ji,j which are, Jxx, Jyy, and Jzz for the magnetic axis in the x, y, and z direction, respectively. Because of the in-plane isotropy in TMDs, we modify the Ji,j tensor by choosing, Jxx = Jyy = J∥ and Jzz = J⊥, with J∥ being the in-plane exchange interaction, and J⊥ being the out-of-plane exchange interaction.

We approximate Ji,j as a function of distance J(r) because we go beyond the nearest-neighbor interaction. The functional form is,

$${J}^{\perp /\parallel }(r)={A}^{\perp /\parallel }\mathop{\sum }\limits_{i = 0}^{3}{c}_{i}{B}_{i}(r)\ h({r}_{{\rm{c}}}-r)+{c}^{\perp /\parallel }\ \exp (-r/\lambda )\ h(r-{r}_{{\rm{c}}}).$$
(2)

Here, h(r) is the Heaviside step function. rc is the cut-off radius within which we approximate the J parameters using B-splines Bi(r)40 with order 3, and outside rc we approximate them using an exponential decay \({c}^{\perp /\parallel }\ \exp (-r/\lambda )\)33,34. Parameters A⊥/∥ and ci are the free parameters. We choose rc to be within the third nearest-neighbor range, which is 7 Å for all the TMDs. Because of the continuity at the boundary r = rc, the parameter c⊥/∥ and λ have an analytical form in terms of the spline functions,

$${c}^{\perp /\parallel }={A}^{\perp /\parallel }\mathop{\sum }\limits_{i = 0}^{3}{c}_{i}{B}_{i}({r}_{c})\exp ({r}_{{\rm{c}}}/\lambda ),$$
(3)
$$\lambda =\frac{\mathop{\sum }\nolimits_{i = 0}^{3}{c}_{i}{B}_{i}({r}_{c})}{\mathop{\sum }\nolimits_{i = 0}^{3}{c}_{i}{B}_{i}^{\prime}({r}_{c})}.$$
(4)

Note that, traditionally, going beyond the nearest-neighbor interaction increases the number of parameters as 2N, where N is the interaction range. For example, for next-neighbor interaction, N = 2, and the total number of Ji,j parameters required to model the magnetic structure is 4. However, in our method, we take into account the exchange interactions up to the 5th neighbor (N = 5). Thanks to the functional form (J(r)) we use, the number of free parameters remains fixed to five. The parameters of the functional form for all the TMDs and the dopant combinations are provided in a separate supplementary document (Supplementary Table 1).

It should be noted that the generalized functional form of the Eq. (2) is useful for materials with in-plane rotational invariance. Materials with broken rotational symmetry require an additional parameter to account for the angular dependence of J(r).

The magnitude of the magnetic moment for the Monte-Carlo simulations are obtained from DFT using

$$| S| =\frac{1}{{N}_{{\rm{c}}}}\mathop{\sum }\limits_{l}\frac{1}{N}\mathop{\sum }\limits_{j}{M}_{{\rm{DFT}}}^{l,j}$$
(5)

Here, \({M}_{{\rm{DFT}}}^{l,j}\) is the average of the magnetic moment of the jth magnetic atom of lth magnetic configuration obtained from DFT. Nc and N are the total number of the magnetic configurations simulated and the magnetic atoms, respectively12.

DFT calculations

All the ab-initio DFT calculations reported in this work were performed using the Vienna ab-initio simulation package (VASP)41,42. The ground state self-consistent field (SCF) calculations were performed using a projector-augmented wave (PAW) potential41 with a generalized-gradient approximation as proposed by Perdew-Burke-Ernzerhof (PBE)43. We have used a kinetic energy cut-off of 450 eV for our DFT calculations. The Brillouin zones were sampled using a Γ-centered k-point mesh of size 5 × 5 × 1 points for 4 × 4 × 1 supercells, and 3 × 3 × 1 points for 5 × 5 × 1 and 7 × 7 × 1 supercells. The TMD supercells doped with transition metals were relaxed until the force on each of the ions was below 10 meV/Å. The energy convergence criterion for the subsequent SCF calculations was set to 10−4 eV.

We have used the Hubbard U model within DFT + U44 to take into account the electron-electron interaction in the d orbital of the magnetic transition-metal atoms. We use the linear response method45 to determine the Hubbard U parameter for the d orbitals of the dopant atoms. The U values we obtain from the linear response calculation are in the range 4 − 6 eV for Ti, V, Cr, Mn, Fe, Co, and Ni-doped TMDs. For the transition-metal and the chalcogen atoms of the TMDs, we use a U = 0 for all their orbitals. We have verified our results by applying a U on the d-orbital of the base transition metal atoms for the TMDs, and our result does not change qualitatively and quantitative changes were small. For example, for Cr-doped MoS2 the near-neighbor anti-ferromagnetic interaction increased by a mere 4% when we applied a U = 4 eV on the Mo atoms.

To obtain Eq. (2) parameters, we place two dopant atoms in a supercell of the base TMD at various positions (near, next, and next-next neighbor) and calculate the total energy of various magnetic configurations. We use supercells of sizes 4 × 4 × 1, 5 × 5 × 1, and 7 × 7 × 1 to calculate the total energies of various magnetic configurations.

Monte-Carlo simulations

We simulate the phase change of the Heisenberg Hamiltonian using Monte-Carlo (MC) simulations. We obtain the critical temperature from the peak of the susceptibility obtained from the MC simulations. The critical temperature was calculated only for the samples with Msat ≥ 0.33 × Mstart, where Msat is the saturation magnetization per dopant atom obtained from MC, and Mstart is the starting magnetization per dopant atom obtained from DFT. To ensure that we capture the effect of configurational entropy, we run 20 separate MC calculations for each material combination and percent atomic substitution, each starting from randomly doped configurations of a 40 × 40 supercell of a TMD. We use a pseudorandom number generator to generate random positions in a pristine TMD lattice, and place the dopant atoms at those positions. We investigate TMDs with an atomic substitution ranging from 6% to 18%. For each randomly doped configuration, we use 1000 equilibration steps, and 1000 MC steps for averaging observables, at each temperature step. For each equilibration and MC step, we perform Natom spin-flip steps, where Natom is the number of dopant atoms in the unit cell.