Abstract
The pioneering paper 'Optical rogue waves' by Solli et al (2007 Nature 450 1054) started the new subfield in optics. This work launched a great deal of activity on this novel subject. As a result, the initial concept has expanded and has been enriched by new ideas. Various approaches have been suggested since then. A fresh look at the older results and new discoveries has been undertaken, stimulated by the concept of 'optical rogue waves'. Presently, there may not by a unique view on how this new scientific term should be used and developed. There is nothing surprising when the opinion of the experts diverge in any new field of research. After all, rogue waves may appear for a multiplicity of reasons and not necessarily only in optical fibers and not only in the process of supercontinuum generation. We know by now that rogue waves may be generated by lasers, appear in wide aperture cavities, in plasmas and in a variety of other optical systems. Theorists, in turn, have suggested many other situations when rogue waves may be observed. The strict definition of a rogue wave is still an open question. For example, it has been suggested that it is defined as 'an optical pulse whose amplitude or intensity is much higher than that of the surrounding pulses'. This definition (as suggested by a peer reviewer) is clear at the intuitive level and can be easily extended to the case of spatial beams although additional clarifications are still needed. An extended definition has been presented earlier by N Akhmediev and E Pelinovsky (2010 Eur. Phys. J. Spec. Top. 185 1–4). Discussions along these lines are always useful and all new approaches stimulate research and encourage discoveries of new phenomena. Despite the potentially existing disagreements, the scientific terms 'optical rogue waves' and 'extreme events' do exist. Therefore coordination of our efforts in either unifying the concept or in introducing alternative definitions must be continued. From this point of view, a number of the scientists who work in this area of research have come together to present their research in a single review article that will greatly benefit all interested parties of this research direction. Whether the authors of this 'roadmap' have similar views or different from the original concept, the potential reader of the review will enrich their knowledge by encountering most of the existing views on the subject. Previously, a special issue on optical rogue waves (2013 J. Opt. 15 060201) was successful in achieving this goal but over two years have passed and more material has been published in this quickly emerging subject. Thus, it is time for a roadmap that may stimulate and encourage further research.
Export citation and abstract BibTeX RIS
1. Foreword
Nail Akhmediev
The Australian National University
This 'Roadmap on optical rogue waves and extreme events' brings together scientists who work in this area of research who would greatly benefit if their efforts are presented in a single review article written by the parties who were able to take part in this adventure. Since the pioneering paper 'Optical rogue waves' by Solli et al [1] started the new field in optics, a great deal of activity on this novel subject has been launched (see, for example [2]), thus, it is time for a roadmap that may stimulate and encourage further research.
Principally the new approach in this roadmap is that the authors of each contribution are allowed to write only two pages on a particular topic. This approach allows us to express succinctly our views on the subject without actually entering unnecessary lengthy details. Another advantage is that it allows the experts to save time in writing their valuable contribution and readers to pick up quickly the new ideas.
While the view of publishing a 'roadmap' was kindly suggested by the Publisher of Journal of Optics, I found the idea exciting and agreed to be the editor. I sincerely hope that this publication will serve as another milestone in developing the concept. The fact that this roadmap will be published in celebration of the International Year of Light 2015 adds to the excitement of this collective endeavor.
We received 14 sections for this article, all written by top experts. Contributions in the roadmap are structured exclusively in the order of their arrival. There is no preference in their arrangement within the article itself. They have been open to each participant of this project in order to review the content. All comments both, open and anonymous, have been taken into account by the authors. This way, the quality of the presentation is kept at the same high level as usual peer reviewed manuscripts submitted to the journal.
I enjoyed reading every single one of them. I hope, the reader will also find it very useful to have many new ideas presented in one place. This innovative way of creating an exciting collective review may become common in future.
Clearly, the roadmap is not a complete review of published papers on rogue waves. However, having a list of such publications may be handy and help the reader in case he/she is interested in a wider range of existing works on the subject. I hope that such a list will be useful and represent the contribution of the authors who for one or another reason could not take part in contributing to the roadmap. I am presenting such a list that covers the years 2014–2015 as the previous literature has been well represented in [2]. These references [3–93] are for short information only and do not have any extended comments on each work. I also hope that the reader will not be harsh on judging the quality of the roadmap if any of the relevant references are unintentionally missing. I stress that the works related to the ocean rogue waves and purely mathematical papers are excluded from this list. It covers only optics and closely related subfields.
With best wishes to all readers,
Nail Akhmediev
2. Optical rogue waves as nonlinear Schrödinger breathers: experiments in optical fibers
Bertrand Kibler
CNRS—Université de Bourgogne Franche-Comté
Status
In nonlinear dispersive wave systems driven by the 1 + 1D focusing nonlinear Schrödinger (NLS) equation, one can address the issue of rogue waves in terms of NLS breathers whose entire space-time evolution is analytically described [94]. For that reason and their 'pulsating' and localization properties, these unstable wave structures were originally considered as the simplest nonlinear prototypes of famous hydrodynamic rogue waves [95, 96]. But they have remained untested experimentally during almost 30 years. They also provide support to the nonlinear stage of the universal modulation (Benjamin-Feir) instability phenomenon, known as precursor of highly localized wave structures through amplification of perturbations (or noise) of (quasi-) continuous/plane waves. Is modelling rogue waves using NLS breathers still a realistic approach?
In confirming their existence and showing that breather dynamics appear even with controlled initial conditions that do not correspond to the mathematical ideal, recent optical studies [97–99] have also extended in some way breather validity towards nonlinear wave systems driven by noise (or with a partial degree of coherence). In such cases, both competition and interaction between many unstable modes take place, so that rogue breathers may appear intermittently or randomly in space and time with associated long-tailed statistics [3, 100]. The latter is a general feature of optical rogue waves identified for rogue solitons in the pioneering work by Solli et al [1]. However, experiments on breathers have been restricted so far to an essentially reduced class of solutions and in the absence of complex dynamics. To go beyond the frontier in terms of testing breathers to model rogue waves, present and future experimental challenges mainly rely on the simultaneous development of ultrafast optical arbitrary wave generation and characterization, and the design of optical systems with controllable complexity, noise and dissipation (i.e., multicomponent and inhomogeneous propagation, as well as integrable turbulence and generalized NLS-based systems, e.g. see sections 3–4, 7, 9, 15). Recent observations of NLS breathers in hydrodynamics [101] have confirmed the direct analogy drawn within the narrowband approximation of NLS model between water waves and light wave propagation in optical fibers, thus making this research area very challenging for both fundamental and applied aspects.
Contribution by the author
Our pioneering studies in optics have shown that breather characteristics are clearly observed even with non-ideal initial perturbations. Indeed, one can check both growth and localization of single breathers that propagate along the optical fiber by using simple initial sideband perturbation to seed the modulation instability process, which corresponds to a time-periodic sinusoidal modulation of the continuous wave [97, 98]. These works concern the simplest first-order solutions that are either periodic in space and localized in time or periodic in time and localized in space; they are referred to as Kuznetsov-Ma breathers and Akhmediev breathers, respectively. By taking the period of both solutions towards infinity, it is possible to approach the limit of the doubly localized Peregrine breather. Note that the standard NLS soliton is also a limiting case of NLS breathers. But this simple experimental technique can lead to the generation of complex behaviors that differ from the expected breather [102]. This gives rise to the higher order modulation instability [103, 104] and stimulation of multiple unstable modes (i.e., nonlinear superposition of breathers that can collide). Theoretically, arrangement in space and time of the nonlinear superposition can be controlled through multiple shifting parameters, which allows generation of an infinite number of possible patterns. Such higher-order breathers are of great interest since they provide higher energy concentration in space and time, and thus localized waves with giant amplitudes.
Consequently, the sensitivity of breather dynamics to initial perturbations depends on the complexity or order of the NLS solution (i.e., the order of energy localization). It is worth mentioning that ideal excitation of breathers in optics are nontrivial to directly synthesize in the temporal domain by means of the usual intensity modulators at gigahertz levels. Note that such GHz-THz frequency bandwidths correspond to the typical instability domain for continuous waves in nonlinear optical waveguides. In this context, we have recently proposed to introduce the advantages of ultrafast optics technology and programmable optical pulse shaping that allow the generation of nearly arbitrarily shaped ultrafast optical wave forms. It is based on spectral line-by-line shaping of a home-made frequency comb generator. Such investigations directly benefit from high-speed telecommunications-grade components. The optical processing based on Fourier-transform pulse shaping provides the ultimate control in terms of phase and amplitude for achieving the ideal excitation of breathers in optical fibers (see figure 1 and [64]). Relative amplitude and phase differences of 25 comb lines are defined from exact conditions given by theory. In general, fiber characteristics (here a standard single-mode fiber) are chosen in accordance with both spectral bandwidth and peak power of the wave evolving into the fiber in order to satisfy the unperturbed NLS model. Either the destructive cutback method or an original approach based on short propagation sequences can be used for reconstructing the full wave longitudinal evolution. Experimental measurements of the synchronized nonlinear superposition of two Akhmediev breathers are in excellent agreement with the theoretical solution, as reported in figure 1. Specific characteristics are revealed such as the time-periodic high-amplitude central peak due to the merging of the two breathers and its associated typical X-shape signature. Note that the growth-decay of the giant peak occurs over less than half of the nonlinear length.
Figure 1. Evolution of two synchronized Akhmediev breathers (i.e., a special case of second-order breather) in both temporal and frequency domains, respectively, as a function of propagation distance and using exact initial excitation. (a)-(b) Experiment. (c)-(d) Theory. Note that dimensional physical parameters are normalized for comparison with theory. (Adapted from [64]).
Download figure:
Standard image High-resolution imageNonlinear coherent structures are also known to emerge or interact from noise, or a 'turbulent' environment with inherent phase randomization (i.e., incoherent waves) in the NLS system [100, 105]. It then appears of fundamental importance to still consider the coherent and deterministic approach to the understanding of rogue-wave phenomena in association with the essential statistical approach of random waves. To that purpose, one has to mention our recent experimental observation of collision between Akhmediev breathers [99], obtained from simple and non-ideal initial perturbations and using a short propagation distance (about 3 nonlinear lengths); this can corroborate the fact that nonlinear coherent structures may emerge locally (i.e., over a few nonlinear lengths) in a turbulent environment. We assume that certain excitation may rarely appear during propagation of chaotic states, which seed the fast nonlinear growth of localized wave structures exhibiting properties reminiscent of NLS breather solutions. In that respect, this experimental work has demonstrated that specific initial conditions are required to lead, with certainty, to efficient collision between breathers at an arbitrary point in space and time, and the appearance of a giant-amplitude wave. In particular, both group velocity and phase differences between breathers govern their mutual interaction, so that the collision event and related giant wave can be easily cancelled. Figure 2 reports the synchronized collision, the qualitative characteristics of the extreme wave are well described by the ideal analytical solution (see also [99]).
Figure 2. Collision of two Akhmediev breathers with non-ideal initial conditions. (a) Theory (i.e., ideal condition). (b) NLSE simulation using experimental conditions. (c) Temporal intensity profile at collision point obtained in experiment and compared to (a) & (b). The main discrepancy observed for the maximal peak intensity is due to propagation loss. (Adapted from [99]).
Download figure:
Standard image High-resolution imageConcluding remarks
These experimental studies in optical fibers have reported the first complete proof of existence and control of the untested class of nonlinear waves called NLS breathers [64, 97–99, 102, 104]. Such waves are of fundamental importance since they contribute to fully describe the growth-decay cycle of extreme localized waves emerging from modulation instability. Note that the physics behind rogue waves discussed here is closely related to the extreme concentration of wave energy compared to the average through nonlinearity and specific local properties of coherence. These parameters are known to play a crucial role in the yet-unresolved challenge of predictability of rogue waves [16, 106, 107].
Acknowledgments and funding information
I gratefully acknowledge past and present collaborators on these experimental works: B Frisquet, K Hammani, J Fatome, C Finot, A Chabchoub, G Millot and J M Dudley, as well as funding from the French National Research Agency and the Conseil Régional de Bourgogne.
I point out that there are numerous papers in wave physics focused on NLS breathers and modulation instability, but only a limited number of references could be included here.
3. Rogue waves in nonlinear multi-component systems
Fabio Baronio
University of Brescia
Status
Nonlinear dynamics is one of the theoretical frameworks that has been successful in predicting the basic features of rogue waves [108]. So far, the focusing nonlinear Schrödinger equation (NLSE) has played a pivotal role as a universal model for rogue wave solutions (e.g. see sections 2, 4). The Peregrine soliton, predicted 30 years ago, is the simplest rational solution of the focusing NLSE with the property of describing localized events in time and space. After decades of debate, the Peregrine soliton has been recently observed in optical fibers, water-wave tanks, and plasmas. Experiments have also shown that breathers and higher-order rational solutions of the focusing NLSE can well mimic extreme wave dynamics (e.g. see section 2).
While rogue-wave investigations are flourishing in several fields of science, moving beyond the standard focusing NLSE description in order to model more general and important classes of physical systems is both relevant and necessary. In this direction, recent developments consist in including higher-order perturbation terms (e.g. see sections 5, 14), because of the high amplitude or great steepness of a rogue wave, in including dissipative terms (e.g. see section 6), since a substantial supply of energy is generally required to drive rogue-wave formation, or in considering wave propagation in higher dimensions.
The study of rogue wave solutions in multi-component wave systems is another hot topic where several advances have been recently reported. Indeed, numerous physical phenomena require modeling waves with two or more components, in order to account for different modes, frequencies, or polarizations. When compared to scalar dynamical systems, vector systems may allow for energy transfer between their different degrees of freedom, which potentially yields rich and significant new families of vector rogue-wave solutions. Rogue wave families have been recently found as solutions of fundamental physical nonlinear models: the vector NLSE (VNLSE) or Manakov system [51, 86, 109–111], the three-wave resonant interaction (TWRI) equations [46, 112], the long-wave-short-wave resonance (LWSW) equations [113], the coupled Hirota equations, the massive Thirring model (MTM) [7]. Multi-component systems have shown to cause wave behaviors that could not be predicted by the scalar NLSE. The existence and properties of rogue waves in multi-component systems is likely to be a crucial step in the understanding and forecasting of extreme wave events in fluid dynamics, optics, plasmas and Bose–Einstein Condensates.
Contribution by the author
Here, we highlight recent original contributions on the existence and properties of rogue waves in fundamental multi-component models, in particular in the VNLSE, TWRI, LWSW, and MTM models.
Over years, the VNLSE has constituted a universal essential vector model for the exploration and description of physical phenomena in several different disciplines. In the context of nonlinear optics, it has been derived for the description of pulse propagation in birefringent fibers, and coupled beam propagation in photorefractive media. In oceanography, the VNLSE describes the interaction of crossing sea currents. Rogue wave solutions of the focusing VNLSE have been recently reported: the vector bright-bright generalization of the Peregrine solution of the focusing NLSE [109], and moreover novel bright-dark rogue structures [110, 111]. Surprisingly, rogue wave solutions of the defocusing VNLSE have also been reported, unattainable in the scalar defocusing NLSE: vector bright-dark and dark-dark rogue waves [86]. Figure 3 reports a typical dark-dark rogue wave in the defocusing VNSLE regime. In addition, recent research activity has also considered higher order rogue waves dynamics in VNLSE, similarly to what was done in scalar NLSE, in order to describe complex high amplitudes extreme dynamics [51].
Figure 3. Dark rogue wave distributions E(1) and E(2) of the defocusing VNLSE [5].
Download figure:
Standard image High-resolution imageThe TWRI model has been extensively studied alongside with the development of nonlinear optics, since it applies to parametric amplification, frequency conversion, stimulated Raman and Brillouin scattering. In the context of fluid dynamics, TWRI applies to capillary-gravity waves, internal gravity waves, and surface and internal waves. In plasma physics, TWRI describes laser-plasma interactions, radio frequency heating, and plasma instabilities. Other important domains of application of TWRI are light-acoustic interactions and wave-wave scattering in solid state physics. Actually, TWRI equations admit families of localized rogue wave solutions. Bright-bright-bright, dark-bright-dark, dark-dark-dark and four-petaled rogue waves structures have been discovered in TWRI equations [112]. Intriguing dynamics of watch-hand like super rogue waves have been also demonstrated [46].
The LWSW equations describe the interaction between a rapidly varying waves and a quasi-continuous one. In fluid dynamics, LWSW resonance results from the interaction between capillary and gravity waves. In optics, the LWSW resonance rules wave propagation in negative index media, or the optical-microwave interactions. Rogue waves have been discovered in LWSW resonance: bright-bright and bright-dark structures have been highlighted [113].
The last model we consider in this survey is the classical MTM, a two-component nonlinear wave evolution model. The MTM is a particular case of the coupled mode equations that describe pulse propagation in periodic or Bragg nonlinear optical media. Furthermore, the coupled mode equations also appear in other physical settings. In particular coupled mode equations describe ocean waves in deep water for a periodic bottom. The fundamental bright-bright rogue wave solution of the MTM has been very recently reported [7]. As such, the search for novel solution forms of these equations, including rogue waves, should provide understanding of unpredictable nonlinear phenomena.
The study of rogue wave solutions in these different multi-component systems contributed to evince peculiar aspects and common features of rogue wave manifestations. It's a well-established fact that, for the scalar NLSE, the focusing regime is a prerequisite for the emergence of regular or random rogue waves. To the contrary, in the scalar case the defocusing regime does not allow for rogue-wave solutions, even of a dark nature. In coupled-wave systems, the focusing regime is not a prerequisite for rogue wave's existence; rogue waves exist also in defocusing regimes [51, 86]. Actually, as far as rogue-wave excitation is concerned, the modulation instability (MI) plays the pivotal role [1, 108]. The conditions under which MI may produce an extreme wave event are subject of intense theoretical and experimental efforts. A rogue wave may be the result of MI (e.g. see section 2), but conversely MI does not necessarily lead to rogue-wave generation. Studies in multi-component systems have shown that the condition for the existence of rogue-wave solutions, in different nonlinear wave models, coincides with the condition of baseband MI [25, 114]. Baseband MI is defined as the condition where a cw background is unstable with respect to perturbations having infinitesimally small frequencies. Conversely, passband MI is defined as the situation where the perturbation experiences gain in a spectral region not including the zero frequency as a limiting case. Figure 4 shows a numerically computed nonlinear evolution, obtained in the case of baseband MI, leading to rogue-wave generation. In the case of passband MI, a train of nonlinear oscillations can be excited, but no rogue waves [25].
Figure 4. Color plot of (a) E(1) and (b) E(2) from the numerical solution of the defocusing VNLSE [25]. The initial condition is a perturbed plane-wave. A dark-bright rogue wave is highlighted by a surrounding box.
Download figure:
Standard image High-resolution imageConcluding remarks
The study of rogue wave solutions in multi-component wave systems is a hot topic of research where several advances have been recently reported. Here, we have highlighted some recent original theoretical contributions on the existence and properties of rogue waves in fundamental multi-component models, in particular we considered the Manakov system, the TWRI equations, the LWSW equations, and the MTM. Moreover, the studies of rogue wave solutions in multi-component systems contributed to evince the regime of baseband MI, as the condition for rogue wave existence. These results shall stimulate the experimental investigations aimed at observing such extreme wave events. The existence and properties of rogue waves in multi-component systems is likely to be a crucial step in the understanding and forecasting of complex wave events in fluid dynamics, optics, plasmas and Bose–Einstein Condensates.
Acknowledgments and funding information
F B acknowledges Shihua Chen for fruitful discussions. F B is supported by the Italian Ministry of University and Research (MIUR, Project No.2012BFNWZ2).
4. Predictable rogue waves
Milivoj Belić1, Wei-Ping Zhong2 and Yiqi Zhang3
1Texas A&M University at Qatar
2Shunde Polytechnic
3Xi'an Jiaotong University
Status
A common understanding is that rogue waves (RWs) are rare extreme localized waves that suddenly appear and disappear in oceans, water tanks, and optical systems [1, 55, 115]. Concerning optical systems, an especially relevant model for describing RWs is the nonlinear Schrödinger equation (NLSE) in various forms. Crucial in the appearance of RWs in NLSE is the modulation instability (MI)—a complex nonlinear optical process that captures the emergence of big waves from small perturbations in initial conditions. MI is very efficient when the waves ride on a finite background. In that respect, very relevant for the generation of RWs appear to be the solutions of NLSE found long ago and appropriately named after the discoverers the Peregrine solitons (PSs) [116], Kuznetsov-Ma [117, 118] and Akhmediev breathers (KMBs, ABs) [119].
It is also believed that statistical analysis, exemplified by the existence of long-tail probability distributions of wave maxima, is necessary for the proper description of RWs. In numerical simulations, RWs emerge from a perturbed background through MI [55], which are then conveniently statistically analyzed. However, we believe that one is not always compelled to perform a statistical analysis of the interfering breathers, to determine which can be considered as RWs. In some models, they may be described analytically and appear at exactly prescribed positions and times. Thus, the emergence of true RWs, towering above the surrounding waves, may be explicitly displayed in analytical solutions that describe nonlinearly interfering solitons and breathers. Nonetheless, one should keep in mind that such RWs are just exact periodic solutions of specific models that do not set the general rules of how to find or describe RWs. In the nonintegrable NLSE models—and most are such—once integration commences from some initial and boundary conditions and the MI sets in, the most appropriate description is statistical.
Still, predictable RWs have been extensively studied [16, 120–122]; check also section 10 of this roadmap paper for a method that, if not predicting at least is anticipating the occurrence of RWs. For example, the management of RWs in inhomogeneous nonlinear media was investigated when the dispersion (diffraction) and nonlinearity were functions of the propagation distance; see also section 15 for a similar treatment. In the general anisotropic inhomogeneous nonlinear media, a more complete treatment takes into account the transverse inhomogeneity of optical media, which is commonly connected with the perturbation in the external potential. This necessitates the inclusion of space-dependent coefficients in the appropriate evolution equation and the treatment by the similarity transformation method.
Contribution by the authors
The model described here, displaying controllable and predictable RWs, is based on the exact second-order breather solutions of the NLSE with spatially-modulated coefficients and an external potential that comes from the change in the index of refraction. Our search for predictable RWs is realized by utilizing the NLSE with a quadratic potential modulated by the diffraction coefficient [120],
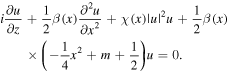
Explicit analytic solutions obtained enable an easier understanding of the formation of RWs. The general solution we find contains two modulation frequencies (the complex eigenvalues) and a modal parameter m, as variable parameters of the second-order breathers, thus allowing one to consider a variety of particular cases with various patterns of such waves. The method is inspired by the paper of Kedziora et al [121], which used a Taylor expansion to study degenerate solutions in the dimensionless standard NLSE without any potential. Another method for finding 3D RWs in parabolic potentials has been advanced in [122]. A method without external potential in 1D is introduced in section 15.
The model we utilize contains variable diffraction and nonlinearity coefficients in the NLSE with a modulated quadratic potential –x2/4 + m + 1/2, in which m is a positive integer [120]. Note that such a 'potential' appears in the parabolic-cylinder differential equation, which will allow the appearance of parabolic-cylinder functions in the solution, once the similarity method is applied. With constant coefficients, the model reduces to Gross-Pitaevskii equation in the harmonic potential, but with variable coefficients and a specific choice of similarity variables it offers hybrid solutions that in addition to the parabolic-cylinder functions contain the solutions of the standard NLSE. By choosing second-order rational breather solutions that ride on a constant background, one discovers the solutions that represent nonlinearly interacting KMBs, PSs, and ABs.
According to the model, there exist four interesting families of the second-order breathers: the nonlinear superposition of two ABs, or an AB and a PS along the x-direction; the superposition of two KMBs, or of a KMB and a PS along the z-direction; the superposition of PSs; and the collisions of KMBs and ABs. Some of those cases are displayed in figures 5 and 6. These cases naturally depend on the values of spatial frequencies and on the modal parameter m. The influence of m is to increase the spread and the number of modes.
Figure 5. Intensities of rogue waves as second-order breathers, viewed as nonlinear superpositions of Kuznetsov-Ma breathers and trains of Peregrine solitons (a) without, and (b) with transverse shifts of the beams.
Download figure:
Standard image High-resolution imageFigure 6. Rogue waves generated when trains of Kuzne-tsov-Ma breathers cross an Akhmediev breather. Note differing intensities of wave trains, with 3 giant peaks towering above the other, when waves strongly interact.
Download figure:
Standard image High-resolution imageAn interesting feature of these waves is that the interacting solitons and breathers can be shifted in the transverse direction, so that one can discern strong effects of nonlinear superposition when the beams strongly overlap. This is evident in figure 5. When the constituent beams interact strongly, the emergence of giant waves is observed, as in the upper panel of figure 5. When the constituent beams are shifted transversely, as in the lower panel of figure 5, they interact less and one sees a resulting wave composed of two pairs of superposed KMB and a train of PSs. No rogue waves are visible. Thus, by changing one parameter, it is possible to observe the appearance of giant waves which otherwise are not seen or expected in the model.
An interesting structure when several KMBs cross an AB is presented in figure 6. Such a second-order rogue wave solution appears when one spatial frequency is imaginary and the other complex. If one chooses m = 2, the wave packet is formed by three KMBs crossing one AB, as displayed in figure 6. In the most general case with complex modulation frequencies, the profiles of second-order breathers are very complex, involving a number of crossing KMBs and ABs but with relatively few RWs towering above the other. Conceptually, our solutions are not much different from the numerical simulation in [55], except that here they are analytic and there chaotic but showing signatures of analytic solutions. Then, a relevant question is, what will a numerical simulation show if one starts the simulation at z = 0 using the exact solution supplied here. Will the exact solution be recovered? The answer is—only partially. Depending on the boundary conditions and the accuracy of the simulation, the exact solution will be followed for a while, but eventually MI will take over and the simulation will resemble the one in [55]. Thus, the existence of periodic solutions does not guarantee their stability or observability.
Concluding remarks
In summary, we have demonstrated predictable rogue waves in the NLSE with a simple quadratic potential modulated by a spatial diffraction coefficient in an inhomogeneous nonlinear medium. The second-order breather solutions, which sporadically but at exactly prescribed positions generate giant localized waves, are constructed by the similarity transformation. Different nonlinear superpositions of KMBs, ABs, and Peregrine solitons are presented by selecting two modulation frequencies and the modal parameter. The controllable behavior of KMBs, ABs, and Peregrine solitons forming second-order breather solutions that contain rogue peaks is displayed.
An important message is that RWs can arise in the analytic interacting breather solutions of NLSE with a modulated quadratic potential. Nevertheless, the importance of modulation instability and statistical description of RWs in the general case should not be underestimated. Our aim was to point out a way to find predictable and controllable RWs that can serve as an appropriate initial point in a more general analysis.
Acknowledgments and funding information
This work has been supported by the National Priority Research Program, project 6-021-1-005, of the Qatar National Research Fund. The work in China was supported by the National Natural Science Foundation of China under grant No. 61275001 and by the Natural Science Foundation of Guangdong Province, under Grant No. 2014A030313799.
5. Rogue waves in passively mode-locked lasers with normal dispersion
Wonkeun Chang1, Jose M. Soto-Crespo2, Peter Vouzas1 and Nail Akhmediev1
1The Australian National University
2Instituto de Optica, C.S.I.C.
Status
Generation of stable pulse trains is important for numerous laser applications where ultrashort optical pulses are needed. Yet, increasing demand for pulses with more extreme characteristics has shifted the focus towards highly nonlinear, non-stationary regimes of laser operation. Of particular interest is the study of the chaotic pulses generated by passively mode-locked lasers. Being an interesting object of nonlinear chaotic dynamics, they may also have important practical applications such as for generating supercontinua without the use of special fibers [123].
One particular type of chaotic pulses that have been reported in various experiments is the so-called noise-like pulses (NLPs), which were first observed in a fiber ring laser [124], and thereafter in various mode-locked laser configurations [125–127]. Experimentally, this regime of laser operation is characterized by its broad and smooth spectrum accompanied by the auto-correlation trace which has a sharp peak sitting on top of a broad pedestal. These features may indicate that there are multiple incoherent pulses that are bunched and traveling together in the laser cavity. However, the chaotic nature of the ultrashort structures in NLPs makes it difficult to experimentally resolve the fine details of the pulse and their shot-to-shot characteristics. Besides, it is not always clear if all reported NLPs refer to the same type of pulses. Thus, more studies are needed in this area.
Relying on numerical simulations is often a more viable approach for investigating these pulses. One of the main techniques used in the modeling of passively mode-locked lasers is the master equation approach [128]. This method averages the effect of the components comprising the cavity, allowing one to study passively mode-locked lasers using a single partial differential equation. It essentially leads to a complex cubic-quintic Ginzburg–Landau equation (CGLE), which admits stable pulse-like solutions.
Contribution by the authors
In its normalized form, the CGLE is given by:
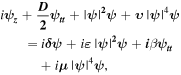
where 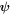 is the complex envelope of the optical field, t is the time in a frame of reference moving with the pulse and z is the propagation distance along the unfolded cavity. The subscripts denote the derivatives with respect to the corresponding variable. On the left-hand side, D denotes the cavity dispersion, being anomalous when D > 0 and normal if D < 0, and ν is the quintic refractive index coefficient. Dissipative terms are written on the right-hand side where δ denotes linear gain/loss, β is the gain bandwidth coefficient, and ε and μ are the cubic and quintic gain/loss coefficients, respectively. The correspondence between these parameters with those of a mode-locked laser system depends on the particular design of the cavity and the mode-locking mechanism [129].
is the complex envelope of the optical field, t is the time in a frame of reference moving with the pulse and z is the propagation distance along the unfolded cavity. The subscripts denote the derivatives with respect to the corresponding variable. On the left-hand side, D denotes the cavity dispersion, being anomalous when D > 0 and normal if D < 0, and ν is the quintic refractive index coefficient. Dissipative terms are written on the right-hand side where δ denotes linear gain/loss, β is the gain bandwidth coefficient, and ε and μ are the cubic and quintic gain/loss coefficients, respectively. The correspondence between these parameters with those of a mode-locked laser system depends on the particular design of the cavity and the mode-locking mechanism [129].
We solved the CGLE numerically for the set of parameters given in the caption of figure 7 using the periodic boundary condition. We obtained a chaotic dissipative soliton with noise-like features as shown in figure 7. Any localized initial condition that is sufficiently close to the solution converged to it after the transient had decayed. This particular soliton consists of a localized background with chaotically appearing spikes on top of it. Only the tails of the solution have a regular exponential decay. The tails do not change much along z. The false color plot of the field amplitude 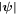 in the (t, z)-plane shown in figure 7(a) clearly demonstrates that spikes appear irregularly across the pulse. These spikes are exceptionally narrow both in t and z direction in comparison to the width of the whole soliton.
in the (t, z)-plane shown in figure 7(a) clearly demonstrates that spikes appear irregularly across the pulse. These spikes are exceptionally narrow both in t and z direction in comparison to the width of the whole soliton.
Figure 7. Chaotic soliton obtained for the CGLE para-meters D = −2.7, ν = −0.002, δ = −0.08, β = 0.18, ε = 0.04 and μ = −0.000 025. (a) Pulse amplitude evolution along z. The amplitude of the spikes exceeds the maximum color scale which is set to 40 for the sake of clarity of the whole pattern. (b) Pulse profiles at two different z, labeled 'b' and 'r' in (a) for blue and red profiles, respectively.
Download figure:
Standard image High-resolution imageThe pulse profiles are plotted in figure 7(b) at two different locations in z, one showing a typical pulse without the spike (blue), and another slice captured when the spike is present (red). The amplitude of the spike is ∼80. This is 5 times higher than the average amplitude of the pulse, which amounts to the intensity amplification factor of 25.
The spikes shown in figure 7 have the main features of dissipative rogue waves studied earlier in [38, 61, 130–133]. Figure 8 presents a probability density function (PDF) of the peak amplitudes in logarithmic scale calculated for the same set of CGLE parameters as in figure 7. The PDF is obtained using the following approach. Firstly, the consecutive profiles separated by the z-interval of 0.02 are found to be completely uncorrelated. As a second step, all local maxima appearing in the chaotic region on top of each pulse profile separated by Δz = 0.02 for 50 different realizations are recorded. Finally, the density of probability was calculated for each value of the amplitude after collecting the data of millions of local maxima. The amplitude slots have been chosen sufficiently small for the curve to be smooth but large enough to have adequate number of data within each slot.
Figure 8. Probability density function (PDF) of the peak amplitudes in logarithmic scale calculated for the same set of CGLE parameters as in figure 7. The black dashed line represents the best fit for the exponential tail of the PDF. The red area corresponds to rogue wave events.
Download figure:
Standard image High-resolution imageThe maximum probability is at around the amplitude of the soliton and decreases at each side of this maximum. The data with very small amplitudes have been removed, and the significant wave-height (SWH) is calculated as the mean amplitude of the highest third of the recorded amplitudes, which is 20.8. Using the definition of rogue waves as the waves that have an amplitude exceeding 2.2 times the significant wave-height, its threshold amplitude is at 45.8. This indicates that all spikes that appear and disappear in this solution are dissipative optical rogue waves.
The elevated tail of the PDF is clearly seen in figure 8. This region corresponds to the chaotically appearing spikes. The probability here is several orders of magnitude higher than that of a simple exponential fit to the main part of the PDF (dashed black line). The total probability of appearance of rogue waves is calculated as an integral of the area below the PDF curve above the rogue wave threshold (shaded in red in figure 8). This probability is found to be 0.003 for the data presented here.
Concluding remarks
A chaotic dissipative soliton with extremely short spikes that appear randomly on its top is an unusual solution of the CGLE. It is very likely that this solution can be found only for normal average cavity dispersion. The PDF of the peak amplitude shows that these spikes have an elevated probability of occurrence, and can be classified as dissipative rogue waves. The whole structure has common features with NLPs but is unique in that the noise-like features are defined by the spikes on top of the soliton.
There may be multiplicity of other types of NLPs in passively mode-locked lasers. One type of them has been presented here. These numerical findings may stimulate experimental observations of such pulses. In the past, many discoveries obtained by solving the CGLE have been observed experimentally. The new solutions presented here can be considered as a first step in the detailed study of a new phenomenon.
Acknowledgments and funding information
The authors acknowledge the support of the Australian Research Council (DE130101432, DP140100265 and DP150102057). The work of JMSC was supported by MINECO under contract TEC2012-37958-C02-02, and by C.A.M. under contract S2013/MIT-2790. JMSC and NA acknowledge the support of the Volkswagen Foundation.
6. Dissipative rogue waves in ultrafast lasers
Philippe Grelu1, Caroline Lecaplain2, and Jose M Soto-Crespo3
1Université de Bourgogne Franche-Comté
2Ecole Polytechnique Fédérale de Lausanne
3Instituto de Optica, CSIC
Status
Optical rogue waves (RWs) are attracting considerable attention, as the possible tabletop counterpart of oceanic rogue waves (see [1] of section 1). While most of the investigations have considered so far the formation of RWs in conservative and integrable systems, there is a recent surge of interest to unveil these extreme wave events in a variety of active dissipative systems, such as in laser cavities [134]. Indeed, active dissipative systems include a sustained supply of energy, which, as the wind for deep-water rogue waves generation, is decisive in the formation of extreme waves. Subsequently, as it has been known for a long time, nonlinearity and high-dimensionality are conducive to the manifestation of chaotic dynamics for certain ranges of laser cavity parameters. The most peculiar chaotic laser dynamics are associated with ultrafast pulse generation (namely, pulses shorter than the response time of fast electronics, below the 10–100 ps range), and can surprisingly be found in the vicinity of the robust and stable mode locked laser dynamics that is the workhorse of ultrashort optical pulse generation [135]. Extreme fluctuations of the pulse energy in a Ti:Sapphire laser were reported in 2011 [130]. On the other hand, several dramatic chaotic dynamics associated with the propagation of transient ultrashort pulses in the laser cavity had already been identified several years ago, see also sections 5 and 12. They include noise-like pulse emission [124], exploding dissipative solitons [136], and soliton rain [137]. With today's hindsight about the ubiquity of extreme wave manifestation among chaotic nonlinear highly dimensional systems, it can be anticipated that subdomains of these dynamical regimes where RWs manifest should be found. However, the real-time characterization that is required to experimentally identify optical RWs among the ultrafast dynamics of chaotic pulses is extremely challenging. Only in the last few years, by using advanced real-time characterization, could optical RWs be singled out in complex ultrafast laser dynamics, see also section 12. It is also remarkable that the important progress made in the characterization of several complex ultrafast laser dynamics not only allowed to deepen their understanding, but also bridged gaps between them.
Contribution by the authors
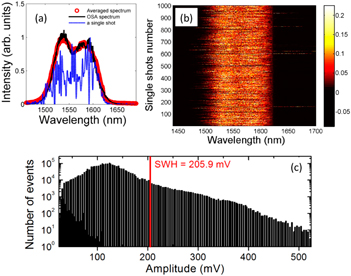
Starting from single pulse mode-locked laser operation, complex dynamics can appear through bifurcations, which can lead to pulsating and chaotic dynamics [135]. Complexity is also exacerbated by the transition from single to multiple pulse dynamics, which brings a myriad of dynamical possibilities owing to the various scenarios of pulse-to-pulse interaction, from pulse bunching, which comprises stationary dissipative soliton molecules, to pulsating and vibrating molecules, and to erratic and chaotic relative pulse motions [135]. In the course of erratic pulse motions inside the laser cavity, nonlinear pulse collisions will take place, which represents a possible route to the generation of transient waves of extreme amplitude. The rate of collisions is likely to be higher when the pulses are confined into a tight packet that propagates round the cavity. Indeed, the experimental existence of a fluctuating bunch comprising tens of pulses—dubbed a liquid soliton phase—was identified as an essential component of the soliton rain dynamics [137]. It was then conceivable that, by a suitable shift of the cavity parameters, bunches of pulses behaving much more chaotically would manifest. To investigate the possibility of rogue wave formation during the propagation of a chaotic bunch of pulses, a detailed numerical study was undertaken, based on a lumped fiber laser ring cavity model [131]. This study predicted that extreme waves should indeed manifest, satisfying the three practical rogue wave criteria, namely (i) their unpredictable appearance and swift disappearance, (ii) their amplitude larger than twice the significant wave height (SWH)—the latter being the mean of the higher one third of the wave events, and (iii) their occurrence exceeding classical distributions. In this case, the route taken to predict RWs went through multiple pulsing, which is favored in an anomalously dispersive laser cavity under intense pumping power, then pulse bunching, a widely represented multiple-pulse behavior, and finally, the destabilization of the pulse bunch that becomes highly chaotic. The related experimental observation faced the major challenge of real-time characterization of ultrafast dynamics. However, some experimental conditions could be found so that the pulse bunch structure could be partially resolved, highlighting in a convincing way the nonlinear pulse collisions that create transient waves of extreme amplitude, which in turn were found to oblige the three main RW criteria [133, 138]. Figure 9 illustrates the detection of one such RW event, in a chaotic bunch whose temporal extent is of the order of a nanosecond. Naturally, the rate of RW detection in the experimental system is highly dependent on the detection bandwidth, as was precisely shown in a detailed subsequent investigation [138]. The reader may also note that another independent prediction of dissipative RW arose from the numerical study of a laser cavity in the normal dispersion regime, starting from the destabilization of high-energy single pulse mode locking [132], see also section 5. Unstable short-pulse propagation in fiber lasers, dubbed noise-like pulse (NLP) regime, has been known for almost two decades [124], but long remained quite mysterious due to the lack of real-time characterization. NLPs generally feature a much shorter temporal extent than the chaotic bunch of pulse illustrated in figure 9, for instance in the range of tens of picoseconds, so that similar characterization is not currently available. However, the similarity between the two dynamical regimes is striking. Consequently, it was recently anticipated that RWs should be found in NLP regimes too [85]. As a matter of fact, real-time spectral measurements were used to reveal the detailed single-shot features of NLP dynamics. In the frame of the dispersive Fourier-transform technique (see section 12), NLPs are considerably stretched using a long dispersive line, so that the spectrum of each pulse becomes mapped into a temporal waveform that is long enough to be resolved by a photodiode connected to a fast real-time oscilloscope. These measurements, illustrated by figure 10, reveal the highly distorted single-shot NLP spectra (see figure 10(a)) that also highly fluctuate from one roundtrip to the next (see figure 10(b)). The probability distribution function of the spectral peak intensity clearly displays extreme spectral events appearing with a rate exceeding that of classical distributions (figure 10(c)). Hence, spectral rogue waves have been recently unveiled within NLP dynamics [85]. Spectral RWs occur in both anomalous and normal dispersion regimes, albeit more prominent in the anomalous ones. It is conjectured that these spectral RWs are the signature of temporal RWs that would manifest in the same dynamical regime, provided that enough real-time temporal resolution would be available for their detection [85]. If correct, it would deepen the connection between NLP and RW dynamics.
Figure 9. Experimental stroboscopic recording of a dissipative rogue wave event at the output of a fibre laser. The laser operated in a chaotic multiple-pulse regime, in the vicinity of mode locking, and its output was analysed with a 45 GHz photodiode connected to a 20 GHz, 40 GSa/s real time oscilloscope. From [133].
Download figure:
Standard image High-resolution imageFigure 10. Spectral rogue waves unveiled from noise-like pulse operation of a fibre laser, using the dispersive Fourier-transform technique for real time spectral measurements. (a) Comparison of single-shot and averaged spectra, (b) evolution of consecutive spectra, and (c) probability distribution histogram of spectral maxima. Adapted from [85].
Download figure:
Standard image High-resolution imageConcluding remarks
From these investigations, using the ultrafast fiber laser as an efficient workbench, a universal class of RWs in dissipative nonlinear systems has emerged. It results from the evolution of a chaotic bunch of pulses or sub-pulses, subjected to numerous collisions. In the near future, it can be foreseen that even more complex RW dynamics will be investigated, involving higher-order dissipative and dispersive physical effects, as well as the polarization degree of freedom into full extent (see section 3 concerning the latter).
Acknowledgments and funding information
We thank N Akhmediev for sustained collaboration on theoretical aspects. Ph G acknowledges support from the Agence Nationale de la Recherche through projects ANR-2010-BLANC-0417-01 and ANR-2012-BS04-001, the Région Bourgogne, and the Labex ACTION program ANR-11-LABX-01-01. The work of JMSC was supported by MINECO under contract TEC2012-37958-C02-02, by C A M under contract S2013 / MIT-2790, and by the Volkswagen Foundation.
7. Rogue waves as natural large fluctuations of the transition to soliton condensation?
K. Hammani1, B. Kibler1, S. Rica2, and A. Picozzi1
1Université de Bourgogne Franche-Comté
2Universidad A. Ibanez
Status
The dynamics of turbulent waves can be characterized by the spontaneous emergence of short-lived high-amplitude waves. Extreme wave events also called rogue, killer or freak waves have been the subject of a tremendous interest in these last years in different physical contexts [1–4, 16, 55, 108]. A variety of mechanisms underlying the emergence of RWs have been identified in the literature, e.g., noise-like pulses in mode-locked lasers (sections 5, 6), or the triggering of RWs from background radiation (section 10), while their control and predictability of occurrence have been analyzed, e.g., in delayed feedback optical cavity schemes (section 8), or through the inhomogeneities of the nonlinear propagating medium (sections 4, 9). In different circumstances, RWs have been also interpreted in the light of exact analytical breather solutions of the integrable 1D nonlinear Schrödinger equation (NLSE), see sections 2–4 and [2, 4, 55, 108]. Breather solutions provide a description of the emergence of individual RW events from a coherent ordered state of the system. On the other hand, RWs are known to spontaneously emerge from an incoherent turbulent state [2, 3, 16, 55, 108, 139–141]. This raises a significant problem, since the description of the turbulent system requires a statistical approach based on the wave turbulence (WT) theory [139], whereas breather solutions describe the emergence of RWs from a coherent environment.
This problem was addressed in the optical context in [140, 141] by considering a specific NLSE model that exhibits a quasi-soliton turbulence scenario, which can be interpreted in analogy with wave condensation: As the amount of incoherence in the system increases, a transition occurs from the purely coherent quasi-soliton regime towards the fully incoherent turbulent regime described by the WT theory [139]. In this context, it was shown that the coherent description of rogue wave events in terms of breather solutions is not inconsistent with the corresponding statistical WT description of the turbulent system [141]. It is important to notice that the emergence of RW events was shown to solely occur near to the transition to (quasi-)soliton condensation. Our aim in this Roadmap communication is therefore to address a possible alternative point of view on the question of the spontaneous emergence of rogue waves from a conservative turbulent environment: Is it possible to interpret such sporadic emergence of RW events as the natural large fluctuations inherent to the phase transition to soliton condensation?
Contribution by the authors
(Quasi-)soliton condensation
We briefly summarize the results reported in [140], in which the phenomenon of quasi-soliton turbulence was studied by considering the representative example of non-integrable NLSE with third-order dispersion effects. From the general perspective of '(quasi-)soliton turbulence' [139], a nonintegrable Hamiltonian system exhibits a thermalization process characterized by an irreversible evolution of the random wave towards an equilibrium state, in which a (quasi-)soliton structure remains immersed in a sea of small scale fluctuations. From the 'microscopic' point of view, this process results from the inelastic collisions among nonintegrable solitons. This eventually leads to the formation of a giant (quasi-)soliton that remains immersed in a sea of small-scale fluctuations which exhibit energy equipartition among the modes. However, in general, the formation of such a large scale coherent structure is only possible if the amount of incoherence in the system is not too large. This aspect has been studied in detail in the context of wave condensation, where the emergence of a large-scale coherent plane wave only occurs below some critical 'energy' [139, 142–144]. The 'energy' refers here to the Hamiltonian, H, which plays a role analogous to the temperature for the microcanonical statistical ensemble considered here. On the basis of these general ideas, [140] reported numerically a 'quasi-soliton condensation' phenomenon characterized by a transition from the coherent quasi-soliton regime toward the fully turbulent regime by increasing the energy H of the system.
As illustrated in figure 11, three different turbulent regimes were identified. For small H, coherent and persistent quasi-soliton structures are generated. For intermediate values of H, non-persistent intermittent-like rogue waves emerge and disappear erratically. For higher values of H, the system exhibits essentially a weakly nonlinear turbulent dynamics characterized by a quasi-Gaussian statistics, so that high amplitude events become extremely rare. The analysis then reveals that the emergence of extreme events occurs essentially in the vicinity of the transition to quasi-soliton condensation, i.e., for H ~ Hc in figure 11. The study also revealed that, because RWs are inherently short and rare events, their coherent description provided by breather solutions is compatible with the WT description of the turbulent wave system [141].
Figure 11. Maximum intensity peak in the simulations of the non-integrable NLSE (with third-order dispersion) by varying the Hamiltonian ('temperature'), H, keeping fixed the power N = ∫ I dt, where I = |Ψ|2. At small H, regime (QS), a persistent quasi-soliton is generated; at high H, regime (WT), the turbulent system exhibits quasi-Gaussian statistics: short-lived RWs events are essentially generated nearby the transition to quasi-soliton condensation, H = Hc ~ 12 [140].
Download figure:
Standard image High-resolution imageFigure 12. Condensation in the defocusing 2D NLSE: Fraction of power condensed in the fundamental mode, N0/N versus Hamiltonian H — in the weak condensation regime (dashed green), and strong Bogoliubov condensation regime (dashed red). Corresponding amount of fluctuations of the condensate fraction, ΔN0 2/N2: Nearby the transition to condensation, H = Hc ~ 2.4, the system exhibits large fluctuations [139, 144].
Download figure:
Standard image High-resolution imageWave condensation in the defocusing regime
There is some correspondence between the mechanisms underlying the formation of a soliton in the focusing regime and the phenomenon of wave condensation in the defocusing regime. The analogy relies on the fact that both phenomena are driven by the natural thermalization of the system toward the most disordered state: it is thermodynamically advantageous for the system to generate a large scale coherent structure (a soliton or a plane-wave) in order to increase the amount of disorder in the form of small scale fluctuations. Actually, the thermodynamic properties of wave condensation are identical to those of an ideal quantum Bose gas, despite the classical nature of the wave system [139, 142]. Wave condensation originates in the thermalization toward the thermodynamic Rayleigh-Jeans equilibrium distribution, whose divergence is responsible for the macroscopic occupation of the fundamental mode of the system.
Large fluctuations
Classical wave condensation is characterized by a 'condensation curve', i.e., the condensate fraction condensed in the fundamental mode versus Hamiltonian. Mathematical expressions for the condensation curve have been derived in explicit analytical form, in both the weakly and strongly (Bogoliubov) nonlinear regimes [142–144]. More recently, the amount of fluctuations of the condensate amplitude at equilibrium has been calculated in both weak and strong turbulence regimes versus the Hamiltonian, see figure 12. The main key result is that the condensate fraction exhibits large fluctuations near by the transition to condensation, i.e., for H ~ Hc, while the fluctuations are significantly quenched in the strongly condensed Bogoliubov regime (small H), and almost completely suppressed in the weakly nonlinear turbulent regime for large H. This result is consistent with the general idea that nearby second-order phase-transitions, physical systems are inherently sensitive to perturbations and thus exhibit large fluctuations. More specifically, it can be shown that, while for H > Hc, the coherence length (λc) at equilibrium remains finite, for H < Hc, it diverges to infinity [λc ∝ 1/(−μ)1/2, where the chemical potential μ → 0− at the transition]. In this case the correlation function does not vanish at large distances, but instead approaches a finite value, lim|r-r'| → ∞ 〈 Ψ(r) Ψ*(r') 〉 → const, which means that the system exhibits long range order and coherence. For H ~ Hc in 2D there is also some evidence of a Berezinskii-Kosterlitz-Thouless transition with an algebraic decay, 〈Ψ(r) Ψ*(r') 〉 ~ |r-r'|−1/4 [145].
Concluding remarks
Numerical simulations of a representative non-integrable NLSE model indicate that extreme events spontaneously emerge from a turbulent state of the system solely in the neighbor of the transition to (quasi) soliton condensation. The coherent description of such short-lived RW events in terms of breather soliton solutions is consistent with the statistical WT description of the turbulent state of the system. On the other hand, the phenomenon of classical wave condensation in the defocusing regime has been shown to be characterized by large amplitude fluctuations of the condensate fraction in the vicinity of the phase transition to condensation. These independent observations indicate that the emergence of RW events can be interpreted as being inherently associated to the natural large fluctuations of the transition to soliton condensation. This may pave the way for a statistical mechanics approach based on the idea of scaling and universal theory of critical phenomena to the description of RWs.
Acknowledgments and funding information
The authors are grateful to C Finot and G Millot for fruitful discussions. K H, B K, and A P acknowledge support from the French National Research Agency (Grant No. ANR-12-BS04-0011 OPTIROC), and the Labex ACTION (Grant No. ANR11-LABX-01-01). S R acknowledges FONDECYT grant N 1130709.
8. Rogue waves induced by delayed feedback in cavity nonlinear optics
Mustapha Tlidi1 and Krassimir Panajotov2
1Université Libre de Bruxelles
2Vrije Universiteit Brussel
Status
The study of formation of rogue waves in nonlinear optics witnessed a sudden acceleration in 2007. This coincides with the experimental evidence of this phenomenon in fiber optics [1]. The explosive growth of this field of research, can be witnessed by recent review papers [2, 55, 108]. Rogue waves are rare events, giant pulses. Often, the long tail probability distribution is the fundamental characteristics accounting for the generation of rogue waves. Note that rogue waves are also called freak waves, killer waves, abnormal waves or extreme events, depending on the authors.
The number of systems in which rogues waves appear is gigantic. Therefore, we have limited the scope of this contribution to transverse nonlinear optics where spatial rogue waves have been observed experimentally [59, 108, 146]. They correspond to large intensity pulses in the transverse directions of a resonant cavity. Various mechanisms have been proven to be responsible for the generation of rogue waves in spatially extended systems. In this paper, we propose a new mechanism based on the optical delay feedback control. For this purpose, we consider a well-known Lugiato-Lefever model equation [147] with delayed feedback. Extreme events induced by optical feedback are discussed in section 10 of this roadmap. In this case, rogue waves appear in the time domain where diffraction is neglected (small area semiconductor laser). Control (suppression) of rogue waves by properly timed seed pulse during supercontinuum generation has been realized in [148].
We demonstrate a way to control rogue waves of light in the transverse section of a broad area nonlinear optical system by means of delay optical feedback. The delayed feedback is found to induce a spontaneous formation of rogue waves. In the absence of delayed feedback, spatial pulses are stationary. The rogue waves are exited and controlled by the feedback. We characterize their formation by computing the probability distribution of the pulse height. Indeed, the long-tailed statistical contribution which is often considered as a signature of the presence of rogue waves appears for sufficiently strong feedback.
The generality of our analysis suggests that the instability leading to the spontaneous formation of rogue waves in a controllable way is a universal phenomenon. Therefore, our mechanism should be applicable to modern high speed semiconductor lasers.
Contribution by the authors
We study theoretically the influence of the delayed optical feedback on the properties of rogue waves formation. We consider a passive cavity filled by a Kerr medium and driven by a coherent radiation beam. The delayed feedback is introduced by an external mirror located at a large distance from the right facet of the Fabry–Perot cavity. The delay time corresponds to the round-trip time in the external cavity. We assume a single-longitudinal mode operation and the reflected field is sufficiently attenuated that it can be modeled by a single delay term. Under these approximations, the dynamics obeys the following well known Lugiato-Lefever model [147] with delayed feedback
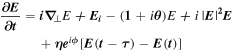
This model equation includes the effect of diffraction in two dimensions described by the transverse laplacian. E is the normalized slowly-varying envelope of the electric field circulating in the optical cavity. θ is the detuning parameter, and Ei is the input field which is assumed to be real, positive and independent of the transverse coordinates. The delayed feedback parameters are the feedback strength η, the phase ϕ, and the delay time τ. Space coordinates are normalized to the diffraction length and diffraction in the external cavity is compensated by a self-imaging feedback configuration.
It is well known that the Lugiato-Lefever equation admits stationary localized structures in one and two-dimensional settings [149] in the absence of delay feedback, i.e., η = 0. The delay feedback allows for the motion of stationary localized structure when the product η τ reaches the value of +1 for ϕ = π [150]. In lasers with saturable absorber localized structures can undergo a period doubling route to chaos [151].
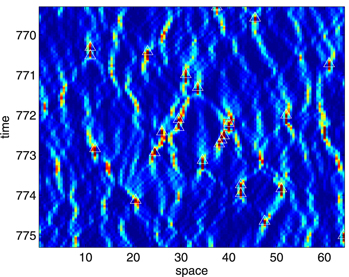
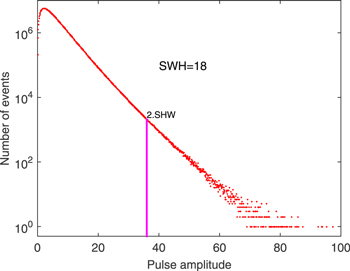
We fix all the parameters and we vary only the strength of the delay feedback. In the absence of delay feedback, i.e., η = 0, single or multipeak stationary localized structures are formed. When increasing the value of η above 1/τ, localized structures exhibit a regular drift with a constant velocity. When further increasing the value of η, rogue waves are formed as shown in the space-time map of figure 13. A statistical analysis shows that their height is more than twice the significant wave height (SWH) as shown in figure 14. This figure shows a non-Gaussian statistics of the wave intensity, with a long tail of the probability distribution typical for rogue waves formation.
Figure 13. Space-time map showing the evolution of optical intensity. Triangles indicate pulses with intensity 5–10 times larger than the stationary localized structures without delay feedback. Parameters are θ = 1.7, Ei = 1.2, η = 0.7, t = 100, and ϕ = π.
Download figure:
Standard image High-resolution imageFigure 14. Number of events as a function of the intensity of pulses in a semi-logathmic scale. Parameters are the same as in figure 13. The SWH denotes the significant wave height. The dashed line indicates 2 x SWH.
Download figure:
Standard image High-resolution imageConcluding remarks
In this contribution we have studied the formation of transverse localized structures and rogue waves in a nonlinear cavity filled by a Kerr medium and driven by an external coherent beam. This simple and at the same time robust device is described by the Lugiato Lefever equation. We propose a mechanism of rogue waves formation based on the time delayed feedback control scheme. We show that the delayed feedback from an external mirror allows the spatial rogue waves to form in the transverse plane of the nonlinear cavity. We have shown that depending on the strength of the delay feedback, localized structures become unstable and rogue waves are formed. We provide a statistical analysis showing a non-Gaussian profile of the probability distribution with a long tail and pulse intensity height well beyond two times the significant wave height.
Our mechanism is rather general and can be applied to modern high speed semiconductor lasers.
Acknowledgments and funding information
This research was supported in part by the Fond National de la Recherche Scientifique (FNRS), the Methusalem project and the Interuniversity Attraction 463 Poles program of the Belgian Science Policy Office, under 464 Grant No. IAP P7-35 Photonics@be.
9. Frozen Akhmediev breathers in dispersion varying fibers
Arnaud Mussot1, Abdelkrim Bendahmane1, Pascal Szriftgiser1, Goery Genty2, John Dudley3, and Alexandre Kudlinski1
1Université Lille
2Tampere University of Technology
3University of Franche-Comté
Status
Rogue waves (RWs) have been observed in many physical systems ranging from hydrodynamics, nonlinear optics or plasma physics to name a few [55]. Since the early experimental observation of RWs in nonlinear fiber systems by Solli et al [1], fiber optics turned out to be an excellent test bed for RW experiments. Indeed, it allows tuning quite easily values of the linear and nonlinear coefficients by simply adjusting the fiber parameters relatively to those of the light sources. For example, the first experimental observations of breather type solutions of the nonlinear Schrödinger equation, widely referred to as RW solutions [55, 108, 152], have been reported in fiber optics. They are generally termed 'Akmediev breathers' (ABs), and constitute a general class of solutions encompassing, the Peregrin or the Kusnetsov-Ma solitons [97, 98]. In most of these studies, linear and nonlinear coefficients are considered to be constant along the propagation axis while it has been theoretically predicted that longitudinal variations of these parameters strongly affects the dynamics of ABs, and thus of RWs [55, 152]. For specific values, it has even been shown that ABs can be annihilated or sustained [154]. As it has already been shown in the context of supercontinuum generation, this new degree of freedom provides a great improvement of their performances [155–158]. In the special context of RWs, it should further contribute to a better understanding/illustration of potential analogies with hydrodynamic RWs as it corresponds to inhomogeneous currents in oceans [108, 153]. A new time, taking advantage of the versatility of fiber optics experiments should improve the understanding of RW formation in the broad sense.
Contribution by the authors
In this work, we show experimentally in an optical fiber system with a tailored longitudinally varying profile that the evolution of ABs can be quasi-stabilized along the propagation direction at their point of maximal compression. This constitutes a first step to show that dispersion managed optical fibers, we called topographic optical fibers [158], can be used to perform such kind of experiments aiming at mimicking very realistic ocean behaviors. Here we demonstrate that ABs can be sustained but other specific dynamics should be observed in our fiber optical system by simply tuning the parameters. Our approach is based on the similarity between compressed ABs and fundamental solitons such that by adjusting the dispersion of the fiber at the point of maximal compression to fulfil the solution area theorem, the evolution can be quasi-stabilized. Figure 15(b) shows an example of the temporal evolution of a theoretical AB in a fiber with uniform dispersion (dashed line in figure 15(a)), displaying the formation of a periodic pulse train at the point of maximal compression (zC = 109 m) before the field recovers its initial state. This single growth-decay cycle with length is a typical signature of theoretical ABs. Spectrally, this dynamic corresponds to a cycle of exponential amplification of harmonics around the pump until zC and their subsequent decay, sometimes interpreted as a manifestation of the Fermi-Pasta-Ulam recurrence [160].
Figure 15. (a) Longitudinal dispersion profiles used in simulations. (b), (d) Simulation of the spatio-temporal representation of ABs in the uniform fiber and in the dispersion-varying fiber, respectively. (c), (e) Corresponding spectral dynamics. Parameters used for simulations: γ = 2W−1.km−1, a = 0.1, amod = 0.05, ωmod = −2π × 400 rad.s−1.
Download figure:
Standard image High-resolution imageIt is worth noting that, at the point of maximal compression zC, individual pulses forming the AB are very close to solitons which are known to be stable time-localized structures. However, since the soliton number associated to the pulses is less then unity [161], the AB keeps evolving after zC and reaches its initial state after further propagation. Our aim being to freeze the longitudinal evolution of the AB, we propose here to adapt the fiber dispersion from zC in order to convert the nearly solitonic AB train into a train of stable solitons evolving independently. As a consequence, we expect to sustain the AB at its point of maximal compression. This soliton conversion is expressed through the soliton number which must equal one. Figures 15(d) and (e) illustrate the possibility of freezing an AB at its point of maximal compression through numerical simulations. They display respectively the temporal and spectral dynamics of an AB in a fiber with an axially varying dispersion coefficient β2 (profile shown in red solid line in figure 15(a)). In this case, the value of β2 at the point of maximal compression zC has been increased to fulfil the fundamental soliton condition [161]. As it can be seen, this simple change of dispersion topography allows to sustain the temporal shape of the AB at its maximal compression state with only a residual modulation of 8% remaining upon propagation. Spectrally, the energy exchange between the different harmonics is significantly affected, as the flow of the energy back to the pump is not observed, i.e. the spectral dynamics is also frozen, on the contrary to what happens in the uniform fiber (figure 15(c)).
We designed and fabricated the uniform and the tapered fibers depicted in figure 15(a), in order to experimentally validate this phenomenon of AB stabilization (see [162] for more details). Our experimental setup has been validated by recording the longitudinal evolution of the spectrum in the uniform fiber (3D plot in figure 16(a)). Black squares in figures 16(c) and (d) show the measured evolution of the power of two input spectral components (the pump and the signal) with fiber length. These results show the progressive depletion of the pump (of 39% of its initial value) and the simultaneous generation of up to six sideband pairs until zC = 107 m. After this point, the energy starts to flow back to the pump as expected from the theoretical AB spectral evolution [55] and from the FPU recurrence [160] in uniform fibers, thus validating our experimental procedure. In a second set of experiments, we investigated the dynamics of ABs in the presence of a longitudinal dispersion step, using the dispersion-varying fiber described above. Figure 16(b) represents a 3D plot evolution of the spectrum along the dispersion-varying fiber obtained from a cutback measurement. Red squares in figures 16(c) and (d) show the measured evolution of the power of the two input spectral components (the pump and the signal) with fiber length in the dispersion-varying fiber. In the first section (within the first 102 m), we observe an excellent agreement with the uniform fiber case. But in the second section (i.e. after the dispersion step), the behavior is now completely different. The energy exchange between the pump and the harmonics is strongly reduced and their respective powers vary much less than in the uniform fiber in the remaining 200 m-long fiber section. However, the AB stabilization observed experimentally is less efficient than the ideal case of figures 15(d) and (e) probably due to small uncertainties on the dispersion step of the fabricated fiber. These results have been compared to numerical simulation of the generalized Schrödinger equation (GNLSE) using the experimental parameters. They are superimposed in figures 16(c) and (d) in solid lines and, as can be seen, a relatively good agreement is achieved that confirmed our experimental measurements.
Figure 16. (a), (b) Cutback measurement of the spectral dynamics of sideband formation in the uniform fiber (a) and in the dispersion-varying fiber (b). (c), (d) Longitudinal evolution of the pump power (black squares) and of the seed (red squares) in the uniform fiber (c) and in the dispersion-varying fiber (d). Solid lines depict GNLSE simulation results (see text for details).
Download figure:
Standard image High-resolution imageConcluding remarks
In conclusion, through an illustrative example of frozen evolution of an Akhmediev breather, we showed that topographic optical fibers can be a fantastic experimental test bed to investigate rogue wave formation in complex systems where one of the parameters evolves longitudinally [162]. We do believe that this new degree of freedom should contribute to another illustration of potential analogies existing between nonlinear fiber optics and hydrodynamics [153], and more generally, to provide a better understanding of rogue waves formation.
Acknowledgments and funding information
This work was partly supported by the ANR TOPWAVE, FOPAFE and LABEX CEMPI (ANR-11-LABX-0007) projects, by the French Ministry of Higher Education and Research, the Nord-Pas de Calais Regional Council and Fonds Européen de Développement Régional (FEDER) through the 'Contrat de Projets Etat Région (CPER)' and the 'Campus Intelligence Ambiante (CIA)'.
10. Accelerated rogue solitons triggered by background radiation
Ayhan Demircan1, Uwe Morgner1, Shalva Amiranashvili2, Carsten Bree2, and Günter Steinmeyer3
1Universität Hannover
2Weierstrass-Institut für Angewandte Analysis und Stochastik
3Max-Born-Institut
Status
The first observation of extreme events in soliton-fission induced supercontinuum generation in nonlinear fibers initiated an ever growing number of publications on optical rogue waves [1], forming a research topic of its own [2]. In fact, extreme event dynamics seems to be much wider spread than originally thought, with similar behavior being observed or suggested in a number of completely different physical phenomena, including various types of water waves and matter waves. Compared to the scarce report of their ocean counterpart, a large number of extreme optical waves can be observed in a fraction of a second. Conditions identified for rogue-wave supporting systems include generic dispersive and nonlinear contributions to the wave velocity, as described by perturbative contributions to the nonlinear Schrödinger equation (NSE), e.g., third-order dispersion. Therefore closed solutions of the NSE given by solitons or Akhmediev-breathers are regarded as building blocks for the generation of rogue events. These events appear due to the inherent modulation instability, which manifests itself in the anomalous dispersion regime of a nonlinear optical fiber. Depending on the propagation dynamics during supercontinuum generation, high-amplitude structures may occasionally be observed at the end of the fiber, with prototypical statistics of rogue waves. Fundamental solitons represent robust solutions of the NSE and extreme events are attributed to extraordinary solitons which have extracted energy within the highly complex propagation dynamics from the system. Collisions between solitons are regarded one of the main mechanisms for the emergence of such a 'champion soliton'. In this scenario, two questions immediately arise: (1) Are there other possible mechanisms leading to the emergence of champion solitons? (2) As the trajectory of the fundamental soliton still appears highly predictable in the overall complex system, how can such solitons be attributed to rogue waves in an unpredictable fashion, especially as solitons are not expected to disappear?
Contribution by the authors
In our investigations, we focus on an interaction phenomenon that has originally been discussed in fluid dynamics as wave blocking between opposing currents [163]. In the optical analogy, a blocking horizon is established by a refractive index barrier by means of the familiar cross-phase modulation (XPM) between two group-velocity matched optical pulses. This kind of interaction builds the basis for the optical push broom effect [164], the soliton trapping phenomenon [165], and the optical event horizon [166–170]. In a fiber with one zero-dispersion wavelength, group-velocity matching (figure 17(a)) can always be realized between a dispersive wave in the normal dispersion regime and a soliton in the anomalous dispersion regime [168]. The basic idea behind this interaction process is creation of a propagating front in the vicinity of an intense soliton traveling in a nonlinear optical fiber. At this front, the propagation velocity of the dispersive waves also changes abruptly. When a co-propagating dispersive wave with nearly identical group velocity approaches that front, this wave cannot pass the soliton front, but is actually thrown back, i.e., a process that has been referred to as reflection of the dispersive wave. An exemplary reflection process at the leading edge of the soliton is shown in figures 17 (b)-(d).
Figure 17. (a) Exemplary group-velocity matching between a soliton (right pulse) and a dispersive wave (left pulse). (b)-(d) Reflection process between the two pulses for a set-up where the dispersive wave approaches the soliton at the leading edge. (b)The soliton is in this case initially slightly faster than the dispersive wave. (c) The dispersive wave cannot penetrate the refraction index barrier. (d) After the collision the dispersive wave is faster than the soliton.
Download figure:
Standard image High-resolution imageIn supercontinuum generation by soliton fission, preconditions for such a reflection process are naturally granted between the ejected solitons and the accompanying generated resonant radiation [167, 168, 169]. A typical example of supercontinuum generation in the time domain is shown in figure 18. The dynamics are described by the nonlinear Schrödinger equation, including the higher-order dispersion as a perturbation. The interaction of the background radiation, relating to phased-matched radiation generated at the fission process, with the first ejected soliton results in a reflection process, as the one shown in figure 17. It is important that dispersive radiation as well as the solitons are strongly affected in this interaction process. Both pulses experience a mutual frequency shift, which manifests itself in the temporal evolution as a change of the group-velocity. In the shown example, the soliton is shifted toward higher frequencies. Any such frequency shift results in adiabatic soliton re-shaping due to a change of the underlying dispersion value. A shift along the dispersion profile towards lower values of the group-velocity dispersion leads to a strong increase of its peak intensity for the soliton. As long as the soliton is accelerated, its intensity continuously increases (red arrow in figure 18). In turn, a strong increase of its peak intensity is induced, which is eventually followed by pulse collapse. This collapse is ultimately unavoidable, given the main preconditions imposed by soliton-fission induced supercontinuum generation, namely the separation of an anomalous and normal dispersion regime. When the soliton spectrum overlaps with the normal dispersion regime, the soliton quickly loses energy to resonant radiation. The faster and stronger the peak intensity increases, the faster a collapse will result. The peak intensity of the giant soliton may achieve intensities more than ten times higher than the solitons that do not interact with the background. In this sense, an accelerated soliton with an extreme intensity fulfills the unpredictability criterion as 'appearing from nowhere and disappearing without any trace'. Compiling the statistics from a total of 4000 realizations of supercontinua using different noise seeds, a heavy-tailed figure-L distribution emerges, as it is characteristic for rare but extreme events. These extreme events therefore exhibit all signatures of rogue waves [167]. In order to investigate the difference to other nonlinear interaction types and energy transferring scenarios given by the optical fiber supercontinuum, the influence of higher-order effects, including the Raman effect, has been studied as well as different possible supercontinuum generation processes [80]. It has been verified that the interaction of a soliton with background radiation may lead to giant solitons, without any soliton-soliton or other interaction mechanism. Finally, in [170], yet another possibility to generate rogue waves by interaction with background radiation is presented. Here an attracting force between two solitons is realized by the interaction with dispersive waves, leading to a fusion of the solitons.
Figure 18. Temporal evolution of supercontinuum generation by soliton fission exhibiting the emergence of an accelerated rogue soliton indicated by an arrow.
Download figure:
Standard image High-resolution imageConcluding remarks
In the original optical rogue wave paper [1], rogue events were attributed to solitons at the end of the fiber. An unpredictability of the extreme events appears due to input shot-to-shot perturbations, leading to different realizations of the supercontinuum generation. However, fundamental solitons may exist over wide propagation distances, and in the measured saturated state no disappearance of solitons is expected. Here, we demonstrate a mechanism to create a 'champion soliton' triggered by background radiation, which is followed directly by its destruction. The concept directly links the presented mechanism to other fields in physics, where analogue systems have been discussed, such as, filamentation matter waves, or hydrodynamics.
Acknowledgments and funding information
We gratefully acknowledge support by The Einstein Center for Mathematics Berlin under project D-OT2, Collaborative Research Center 123 PlanOS, and Nieders. Vorab Z3061.
11. Extreme optical pulses in semiconductor lasers
C Masoller
Universitat Politecnica de Catalunya
Status
Semiconductor lasers emit a stable output unless they are optically perturbed. When they are under the influence of continuous-wave (cw) optical injection or under the influence of optical feedback from an external reflector, they can display a rich variety of dynamical behaviors, including periodic oscillations, chaos, excitability, mode competition, etc. Besides the practical interest for applications, the laser dynamics is relevant from the nonlinear perspective and has been intensively studied, both, experimentally and by model simulations. While a lot of effort has focused on the chaotic and excitable regimes, less attention has been paid to regimes where the laser intensity displays rare and extreme pulses [1].
Contribution by the author
In the last few years we have investigated extreme optical pulses in the output of semiconductor lasers under cw optical injection [49, 69, 134, 171] or under optical feedback [172]. We have used a simple rate-equation model that, in the case of feedback, includes a time-delayed term representing optical feedback. In the case of an injected semiconductor laser, we have shown that in narrow parameter regions (within the chaotic region) the laser intensity occasionally displays ultra-high, extreme pulses (i.e., pulses which belong to the tail of an l-shaped distribution of pulse heights), which were identified as deterministic optical rogue waves (RWs) [134]. In the feedback case, we have also identified narrow parameter regions where the intensity displays extreme pulses [172].
Several mechanisms are capable of explaining the emergence of such extreme pulses [90, 108]. In the case of optical injection, we found that the mechanism generating extreme intensity pulses is a process that resembles an external crisis, in the form of a crossing of the chaotic attractor generated from one fixed point with the stable manifold of a saddle point (this stable manifold acts as a 'barrier') [171]. After crossing the barrier, the trajectory can approach the region of the phase space where the stable manifold of a third unstable fixed point is located, and each time the trajectory closely reaches this narrow channel, an ultra-high pulse is triggered (thus, we refer to this region of the phase space as the 'rogue wave door').
A similar mechanism for the generation of extreme events has been reported in a system of coupled excitable units [173], where there is a narrow channel-like structure in phase space that is occasionally entered by the system, and that when entered leads to a long excursion in phase space, which constitutes the extreme event.
A comparison of the behavior induced by self-optical feedback with that induced by cw injection from a master laser suggests that, despite the differences in both situations, the extreme pulses in the feedback case, figure 19, occur through a similar mechanism: the presence of a narrow channel in the phase space.
Figure 19. Simulated time series of the intensity of a semiconductor laser with optical feedback and phase portrait displaying the superposition of several sections of the trajectory that contain extreme pulses. Adapted from [175].
Download figure:
Standard image High-resolution imageMoreover, both, in the injection case and in the feedback case, a clear pattern of oscillations anticipate the most extreme pulses (see figure 20). We have recently demonstrated that advanced tools of symbolic time-series analysis can be used to anticipate abrupt stochastic switchings, and specifically, the polarization-switching of vertical cavity surface emitting lasers (VCSEL) [174]. We speculate that this symbolic analysis tool could also be useful for providing an early-warning indication of the occurrence of an extreme pulse.
Figure 20. Superposition of several simulated extreme optical pulses generated by an optically injected semiconductor laser (top; adapted from [171]) and by a semiconductor laser with optical feedback (bottom; time is units of the feedback delay time, adapted from [172]).
Download figure:
Standard image High-resolution imageBesides the prediction of extreme optical pulses, a relevant challenge is to identify key parameters that are able to increase or to decrease their likelihood of occurrence, i.e., to control them. In the optically injected laser, our model simulations suggest that one crucial parameter is the noise strength: for parameter regions where deterministic RWs occur, the inclusion of noise in the simulations significantly decreased the number of RWs [69]. This is due to the fact that noise tends to drive the trajectory away from the phase-space region where RWs can be triggered (i.e., where the RW door is). On the other hand, for parameters such that there are no deterministic RWs, but close to the region where they occur, then, the inclusion of noise in the simulations anticipates the RWs. This is due to the fact that noise allows the trajectory to cross over the 'barrier' and thus, noise allows the trajectory to access the phase space region where the RW door is, therefore, occasionally extreme pulses are triggered.
As is well known from chaos control theory, the periodic modulation of an appropriate control parameter can stabilize unstable periodic orbits and thus, suppress chaos. We have investigated via model simulations if external modulation can also be an effective way to suppress extreme pulses. We have focused in current modulation, as this is straightforward to implement experimentally. In injected lasers our model simulations suggest that RWs can be fully suppressed by current modulation of appropriated amplitude and frequency [69]. When the pump current is modulated at a frequency, fmod, close to the laser natural resonance frequency (the relaxation oscillation frequency, fro, of the free-running laser), then, the modulation is capable of fully suppressing the extreme pulses. This is due to the fact that weak modulation increases the regularity of the amplitude of the pulses: the number of large pulses in the time series increases, but at the same time, the pulses are less extreme.
If the modulation is slower than the resonance frequency (fmod < fro), the RWs occur within a well-defined interval of values of the modulation phase, i.e., there is a 'safe' window of modulation phases where no RWs occur [49]. The most extreme RWs occur for modulation phases that are at the boundary of the safe window. When the modulation is fast (fmod > fro), there is no safe phase window; however, the extreme pulses are likely to occur at specific values of the modulation phase [49].
The role of current modulation in the feedback case is now being investigated, and we speculate that modulation of appropriated frequency will also be able to suppress the extreme pulses.
Concluding Remarks
A relevant question is whether these observations can be exported to other systems, i.e., if our results could be relevant to the study of real-world high-dimensional complex systems that generate extreme fluctuations in their output signals. In particular, our findings on the role of noise and periodic current modulation for suppressing extreme pulses could be of interest for the control of extreme events in other systems, where a similar response to noise or modulation could be observed. We also hope that our numerical results will motivate experimental investigations to confirm the numerical prediction regarding the role of current modulation in providing 'safe phase windows' where the likelihood of RWs is very small.
Acknowledgments and funding information
This work has been supported in part by the Spanish MINECO (FIS2015-66503-C3-2-P) and ICREA ACADEMIA.
12. The fastest gun in the west---how single shot measurements are transforming the search for rogue waves
Neil G R Broderick, Antoine F J Runge, and Miro Erkintalo
University of Auckland
Status
The investigation of extreme events in optics, or optical rogue waves, is of interest for both fundamental and applied studies. In the fundamental arena, rogue waves represent new solutions to old equations, and they have applications across many areas of science. It is then the hope that, once the events are better understood, they can be harnessed and used. Crucial to elucidating the underlying physics is the ability to perform real time single shot measurements. This is because rogue events are by definition transient and statistically rare; conventional time-averaged measurement techniques cannot reveal their full details.
Contribution by the authors
Our investigations into extreme events in optics was motivated by the observations of instabilities in passively mode-locked fibre lasers [175, 176]. Specifically, we observed instabilities in both Yb- and Er-doped fibre lasers that displayed qualitative similarities, despite the laser devices possessing opposite signs of the cavity dispersion. When diagnosed with a conventional optical spectrum analyser, the unstable pulse sequences exhibited a smooth, broad spectrum, whereas when operating in the stable regime the spectrum was highly structured (e.g. strong Kelly sidebands in the soliton regime). These unstable modes of operation correspond to the 'noise-like' pulse regime as originally identified by Horowiz et al in 1997 [124], and subsequently found by many other researchers.
Noise-like pulses can display rogue wave –like characteristics. Indeed, in 2011 two research groups independently demonstrated, using numerical simulations, that chaotic dynamics in passively mode-locked laser can give rise to 'dissipative optical rogue waves' [131, 132]. Later that same year, Kovalsky et al considered a solid-state Ti:Sapphire laser, and reported the first experimental observation of extreme value events in a mode-locked laser [130]. In 2012, Lecaplain et al reported experimental observations of dissipative rogue waves in a passively mode-locked fibre laser [133].
In prior experimental studies [130, 133], dissipative laser rogue waves were analysed predominantly in the time-domain. However, it is well-known that frequency-domain analyses are important for the full characterization of rogue events [1]. Therefore, to examine dissipative rogue waves in the frequency-domain, we have developed and applied single shot spectral measurement techniques. In particular, conventional spectral measurement techniques are much slower than the repetition rate of ultrafast lasers. As a consequence, results from such measurements correspond to ensemble averages over thousands of pulses. It should be clear that these measurements cannot properly measure transient effects, such as rogue waves, and therefore new measurement techniques are called for.
In our laboratory, we have made extensive use of the dispersive Fourier transform (DFT) [177] in order to measure shot-to-shot spectra of pulses emitted by ultrafast lasers. The DFT makes use of the fact that, after a sufficiently long propagation distance in a dispersive medium, the temporal shape of a pulse evolves into a copy of its spectral shape. This occurs because every frequency travels at a different speed thanks to group-velocity dispersion. Thus, all that is needed for real time spectral measurements is a long length of fibre and a comparatively fast photo-diode, connected to a real-time fast oscilloscope. Adopting this tehnique has allowed us to demonstrate that the smooth spectrum characteristic to noise like pulses results from the averaging effects and that each individual spectrum is, in contrast, highly structured [175, 176]. Most recently we have used this technique to study soliton explosions [136] (see figure 21) and other transient effects in fibre mode-locked lasers.
Figure 21. Example of a Soliton Explosion, at different roundtrip numbers, recovered via single shot spectral measurements (see, for example, [136]).
Download figure:
Standard image High-resolution imageOur single shot measurements [61] (see for example figure 22) and the work of others have also confirmed that rogue waves can 'hide' inside otherwise noisy data [133, 178]. In our laser, the presence or absence of extreme fluctuations can depend on where in the cavity the output coupler is located, and what spectral region is investigated. These results thus show that, in these dynamic devices the pulse and indeed its statistics change dramatically during propagation around the cavity. This is not surprising given the highly nonlinear nature of light propagation in a fibre laser and highlights the unique potential of fibre lasers as a testbed for a wide range of nonlinear effects.
Figure 22. Statistics of Raman Rogue waves in our fibre laser (see [61] for details).
Download figure:
Standard image High-resolution imageWhile the DFT can illuminate many aspects of extreme fluctuations in fibre lasers, it cannot tell the whole story. In particular, we lose phase information when measuring the spectrum using a photodiode and so cannot reconstruct the temporal shape of the pulses. To gain further insight into their temporal coherence characteristics, we interfered two consecutive pulses in a Michelson interferometer and observed no sign of any coherence [176]. These measurements imply that the pulses vary completely from one round trip to another, providing additional impetus for future single-shot measurements.
Concluding remarks
Unlike most pulse formation processes in optics, the generation of optical rogue waves results in a series of unique events. Their study has resulted in a surge of interest in real time measurement techniques. The continual development of both measurement techniques and theoretical models of pulse formation is sure to lead to new advances in photonics in years to come. We note that already at least one company is selling instruments designed to look at optical rogue waves based on real time spectral measurements [179]. Although our work has focused on pulse formation in fibre lasers, the obtained result may also be applicable to other systems, such as supercontinuum generation [1] or Raman amplification [178], where optical rogue waves can also occur. This work also highlights the potential of passively mode-locked fibre lasers to serve as a model nonlinear system whose output can mimic many other systems of interest.
Acknowledgments and funding information
The authors gratefully acknowledge funding from the Mardsen Fund of New Zealand.
13. Rogue waves in multimode optical systems
S Residori1, U Bortolozzo1, and F T Arecchi2
1Université de Nice-Sophia Antipolis, CNRS
2Università di Firenze and CNR-INO
Status
'Rogue waves', considered as part of maritime folklore, was the name given to the erratic giant waves spontaneously occurring on the ocean surface, as the sudden appearances of a vertical wall of water preceded by a trough so deep like a 'hole in the sea'. Despite the extremely dangerous character of these phenomena, the scientific community remained mostly silent until the first 'measurement' was unequivocally reported during the famous rogue wave of 1 January 1995 at the Draupner platform off the coast of Norway. Since then, rogue waves, previously considered near-mythical, were recognized as real physical phenomena and the field of investigation has been constantly growing, not only in oceanography but in many different contexts, wherever waves are concerned independently of their physical origin. The burst of investigations has, then, involved hydrodynamics, optics, plasmas, acoustics, superfluids, Bose-Einstein condensates, to cite a few, and the basic physical concepts have grown on a multidisciplinary ground, promoted by laboratory-scale experiments and by the development of general models and mathematical tools [108, 176, 180]. In optics, the concept of rogue waves was proposed in the seminal work of Jalali group for the peaks appearing in the supercontinuum generated by a photonic crystal fiber [1]. Optical rogue waves constitute now a subject of investigation on its own and have been reported in a variety of optical systems. Besides, the analogies and links between optics and water waves are particularly favored because the two domains have in common the Nonlinear Schrödinger equation, NLSE, one of the fundamental equations in nonlinear physics. Numerical simulations also play an important role in shedding light on basically involved mechanisms, as Benjamin-Feir instability, emergence of large breathers, large filaments in wave turbulence. Some common features of these wave phenomena, as the large deviations from the Gaussian statistics of the amplitude, the existence of many uncorrelated 'grains' of activity and their clustering in inhomogeneous spatial domains, are now well established. As for a universal definition or a general classification in terms of different statistics and nature of the involved waves, this still constitutes an ongoing process continuing to stimulate an increasing number of new investigations.
Contribution by the authors
Optical rogue waves have been analyzed in the context of different multimode systems, characterized by different degrees of nonlinearity and having in common the excitation of many spatial modes. The first experiment consists of a unidirectional ring oscillator with a liquid crystal light-valve, LCLV, acting as the gain medium. Photons are injected in the cavity through a wave-mixing process occurring in the liquid crystal pumped by an incoming laser beam. While for low pump intensity the amplitude of the cavity field follows a Gaussian statistics, for high pump we observe the emergence of spatiotemporal pulses with much higher amplitude with respect to the background, that develop erratically in time and in space and live for a typical time of the same order of the response time of the LCLV [182]. The optical rogue wave phenomenon is characterized by measuring the probability density functions, PDF, of the light intensity (figure 23). Because an exponential statistics for the intensity corresponds to a Gaussian statistics for the field amplitude, an exponential PDF of the intensity is characteristic of a speckle pattern, where each point receives the uncorrelated contributions of many uncoupled modes. At low nonlinearity, indeed, this is the behavior displayed by the cavity field. However, because of the geometry of the resonator, the modes are nonlocally coupled and when the intensity of the pump laser increases the nonlinear coupling leads to a complex space-time dynamics with extreme events populating the tails of the PDF and providing large deviations from Gaussianity [183]. The PDF are well fitted by a stretched exponential function with the amount of stretching increasing when increasing the pump intensity, hence, the nonlinearity. If the nonlocality is removed by changing the geometrical configuration of the resonator, the statistics becomes Gaussian again, demonstrating the importance of the nonlocal coupling in the generation of the optical rogue waves [108, 183]. In a second experiment, we feed a multimode optical fiber with light focused on the entrance by a large numerical aperture lens [184]. Here, the minimal size of the optical grains is due to the diffraction limit of the input beam, while nonlocal coupling is provided by an asymmetric mask provided by a spatial light modulator that selects asymmetrically the wave vectors coupled inside the fiber (figure 24). A time dependent mechanical perturbation n(t) is applied to the fiber in order to induce a dynamical behavior. The intensity of the light distribution at the exit of the fiber exhibits a stretched exponential statistics depending on the degree of inhomogeneity introduced by the SLM. Rogue waves in the absence of nonlinearity have also been reported in microwave experiments [185]. The emergence of high amplitude filaments has, then, been studied in a one-dimensional liquid crystal experiment, in which an optical wave turbulence [186] regime has been realized [187]. The laser beam is shaped as a laminar beam and propagates longitudinally inside the liquid crystal layer. By using a SLM, spatially random phases are imposed as the initial condition. Large amplitude filaments are formed after the inverse cascade, when modulation instability of the wave condensate sets in [187, 188]. The results of all the above investigations show that nonlinearity and nonlocal coupling play a key role in originating rogue waves. In this context, the linear experiment has the role of highlighting the essential role of granularity, that is, the fragmentation of the optical field in fundamental grains of activity. It must be stressed that in all the considered systems rogue waves are the result of the dispersive properties of ensembles of many waves. In these systems, the nonlinearity needs not necessarily to be strong, provided that the nonlocal coupling plays its role of mixing-up the individual grains of activity [108].
Figure 23. Probability distribution function (PDF) of the cavity field intensity; the nonlinearity is increased from the steepest to the shallowest distribution; inset: instantaneous profile of the cavity field intensity. From [182].
Download figure:
Standard image High-resolution imageFigure 24. (a) Multimode fiber setup. (b) Spatial light modulator (SLM) transmission mask, (c) speckle patterns and (d) corresponding intensity distributions at a selected y-coordinate. (e) PDF of the intensity; inset: Gaussian PDF of the perturbation n(t). Adapted from [108, 184].
Download figure:
Standard image High-resolution imageConcluding remarks
Optical rogue waves appear as genuine space-time phenomena in multimode optical systems. A wide aperture cavity and a multimode fiber have been presented as prototype experiments. In both systems the optical field is characterized by stretched exponential statistics of the intensity, emergence of individual grains of activity and grain clustering in inhomogeneous spatial domains. In between the cavity and the multimode fiber a weakly nonlinear wave turbulence regime has been studied for light propagating in a liquid crystal medium. Non-Gaussian statistics of the amplitude and the formation of large amplitude filaments have been observed in the wave condensation regime [188]. All these results suggest that in presence of a large number of nonlocally coupled waves the nonlinearity does not have to be necessarily large in order to provide rogue wave phenomena.
Acknowledgments and funding information
The authors acknowledge the ANR international program, project ANR-2010-INTB-402-02, 'COLORS'.
14. Guided wave optics testbed for exploring extreme weather events and power grid stability
Stefan Wabnitz
University of Brescia
Status
There are many phenomena in physical and social sciences that are described in terms of the same universal statistical distributions, and which are characterized by the presence of extreme events, associated with the properties of the tail end of these distributions. Consider for example hydrodynamics (turbulence, hurricanes, tsunamis), geosciences (earthquakes, floods, landslides), economics (financial markets), social sciences (distributions of populations), medical sciences (neuronal avalanches, epileptic seizure), material failures, power grid and computer networks (black-outs), environment and climate sciences (forest fires, evolution and competition of animal and plant species). There is an ongoing philosophical debate as to consider these extreme events as essentially unpredictable, as stated by the so-called black swan theory, which can be seen as an out spring of the concept of self-organized criticality.
Such a viewpoint is inherently pessimistic, as the lack of predictability entails a lack of accountability for the scientist who was unable to predict the occurrence of the extreme event. On the other hand, there is an emerging theory of extreme events that associates their presence to the generation of coherent wave structures, such as for example nonlinear waves or solitons, which do not belong to the same population of random linear waves. Hence the appearance of extreme events in the form of solitons is subject to their own 'dragon-king' statistical distribution [189]. The important consequence of this point of view is the predictability of the occurrence of the extreme event, based on the observation of a suitable precursor. This entails even the possibility or controlling or even suppressing the emergence of the extreme event [148], if the observation of precursors was able to trigger a proper feedback signal.
Of great interest today is the study of the mechanism of extreme or rogue waves in oceanography in the regime of shallow waters, where catastrophic damages may be produced by the on-shore arrival of a tsunami. Another hot topic that is the subject of extensive investigations is the emergence of irregular and extreme events in coupled nonlinear oscillator systems such as the power grid distribution network [190]. In this case, it has been recently proposed the use of the Ginzburg-Landau equation to describe coupling among the grid of nonlinear oscillators [191].
Contribution by the author
The purpose of this contribution is to highlight the use of optical fiber and waveguide experiments, where optical pulse propagation can be modelled by simple, and yet universal nonlinear evolution equations (e.g., the nonlinear Schrödinger equation (NLSE), the nonlinear shallow water equation (NLSWE), the Ginzburg Landau equation (GLE), as a simply accessible test bed for exploring, in a well controlled manner, the dynamics of complex phenomena that exhibit extreme events. Thus nonlinear guided wave optics provides a practical platform for the accessible statistical study of extreme event generation in the diverse domains of science and applications such as discussed in the status sub-section (as first proposed in [1]).
Among these, let us discuss at first the possibility of exploring, by means of fiber optics experiments, the dynamics and the control of extreme weather events such as ocean tsunamis. In the case of normal group velocity dispersion, and whenever the input pulse is such that the associated nonlinear length is much smaller than the dispersion length, it is possible to reduce the description of pulse propagation from the NLSE to the NLSWE [192]. Let us recall that in hydrodynamics the NLSWE describes the propagation of water waves in shallow water, which is the regime were the wavelength of the waves is much longer than the depth of water. A typical and well-known example of shallow water wave with catastrophic consequences is the tsunami. The optical pulse intensity corresponds to the height of the water wave, and the optical frequency corresponds to the wave velocity. Therefore one may study by means of a suitably prepared input optical pulse, and a properly engineered optical fiber, the phenomenon of the run-up of a tsunami towards the beach [192].
The NLSWE possesses several exact solutions, among which of particular interest are the so-called Riemann waves, which describe unidirectional propagation and reshaping until a vertical profile is reached (shoaling) of a wave possessing an initial velocity profile that is proportional to its amplitude. In fiber optics, the propagation of a Riemann pulse with an initial hyperbolic secant shape is depicted in figure 25 (top plots). Here we compare the initial intensity (red dashed curves) with the intensities resulting from the exact solution of the NLSWE (green traces) and the numerical solution of the NLSE (blue traces). Note that the NLSE predicts the appearance of a shock wave (high frequency temporal oscillations) after the shoaling point.
Figure 25. F Shoaling of optical Riemann wave (top); rogue pulse generation in a fiber loop (bottom). Reproduced from [192].
Download figure:
Standard image High-resolution imageIt is very interesting to consider pulse propagation in the shallow water regimein a fiber loop, in the presence of a modulator that imposes a continuous frequency shift of the carrier frequency. In this case the frequency shifting is analogous to the presence of a sloping beach for ocean waves. This situation may lead to the appearance of high intensity and temporally compressed extreme pulses (see figure 25, bottom picture) [192]. This leads to the intriguing possibility of mapping the depth of the shoreline into an appropriately designed modulator driving, for mimicking the emergence of catastrophic wave events by means of harmless laser optics experiments.
In shallow waters, giant waves (also known as sneaker waves) may suddenly appear near the beach as the result of the collision of oppositely directed currents. In fiber optics, the analogous phenomenon results by launching into the fiber a CW with a periodic modulation of the initial frequency (or phase) [193]. The experiment has led to the observation of the generation of giant pulses with a flat-top intensity profile, or optical flaticons [194].
Another intriguing example of complex physical dynamics, which is readily accessible via the fiber optics platform, is the analysis and control of chaotic coupled nonlinear oscillators. A typical example is provided by the nonlinear dynamics of coupled polarizations in fiber lasers. Based on the common mathematical description provided by the coupled GLEs, these studies may suggest for example novel routes for achieving the robust stabilization against blackouts in the power grid.
The spatio-temporal analysis of fiber laser emission has very recently unveiled the presence of intermittence phenomena that separate laminar or regular pulse emission states from chaotic pulsations [195]. A universal description of the transition from mode locked regime into space-time laser turbulence may be obtained in the frame of the GLE [196]. In vector fiber lasers, nonlinear polarization coupling may lead to synchronization of the irregular, uncorrelated intermittent emission (see an example in the top panels of figure 26) into regular domains of alternating states of polarization, or polarization domains, separated by polarization domain wall solitons [197].
Figure 26. Spatio-temporal intermittency (top) and polarization rogue waves in a fiber laser (bottom).
Download figure:
Standard image High-resolution imageMoreover, coupled GLEs describe extreme events that emerge from the nonlinear coupling between a Stokes and a pump wave in fiber Raman lasers [198]: e.g., the polarization rogue wave in the bottom plot of figure 26.
Concluding remarks
Nonlinear optics experiments provide a powerful means to mimic and explore the nonlinear dynamics of coherent structures that may be generated as extreme events from the propagation of laser pulses in the presence of a noisy background. One remarkable property of optical fibers is the possibility of engineering their parameters (e.g., dispersion, nonlinearity) along the longitudinal dimension, whereas the amplitude and phase of the input pulse may also be precisely tailored. Moreover, the continuous monitoring with advanced data processing techniques of the re-circulating output of fiber lasers permits nowadays the extraction of an unprecedented amount of statistical properties that characterize the extreme dynamics of extended nonlinear coupled oscillator systems. The new frontier of nonlinear optical guided waves for the study of extreme events is going to be the extension beyond 1-dimensional propagation, e.g., waveguide arrays, multimode fibers, and transverse spatio-temporal effects.
Acknowledgments and funding information
S W thanks in particular A Mussot, C Finot, Ph Grelu, D Churkin, B Wetzel and R Morandotti for insightful discussions. This work is supported by the Italian Ministry of University and Research (MIUR, Project No.2012BFNWZ2).
15. Generation of multiple compression points for Akhmediev breather with periodic coefficients
C G Tiofack, S Coulibaly and M Taki
University of Lille
Status
Rogue waves (RW) are short-lived phenomena appearing suddenly out of normal waves and with a small probability. These are extraordinarily high amplitude localized wavelets, whose height exceeds many times the height of surrounding waves. There has been growing interest in studying RW in many dispersive media e.g. nonlinear fibre optics, Bose-Einstein condensations, super fluids, space plasma etc [1, 55]. It was shown at a very early stage that exact breather-type solutions of the nonlinear Schrödinger equation (NLSE), well known to govern the nonlinear propagation of modulated wavepackets in various physical contexts [199], reproduced the qualitative characteristics of freak waves to a highly satisfactory extent. The pioneering works by Peregrine [116], Kuznetsov [117], Ma [118] and Akhmediev [199], succeeding to construct an analytical toolbox for freak waves whose relevance was later established experimentally in different frameworks [97]. Akhmediev Breathers (ABs) are coherent structures that oscillate in space or time and have the peculiarity of changing their amplitude as they propagate. They have been considered in various fields of physics as a plausible object that describes the formation of RW [152]. It is well known that the dynamics of ABs is strongly affected in the presence of varying dispersion and/or nonlinearity [153, 200]. Recently, the experimental observations of ABs have been reported in optical fibers and it was shown that their evolution can be quasi-stabilized in space at their point of maximal compression for a properly designed fiber with longitudinally varying profile [162]. However, RW are elusive and intrinsically difficult to monitor, thus a full understanding of them is far from having been achieved and deserves further careful study. In particular, important questions arise when investigating the formation of RW under periodic modulations in parameters. How to control the generation of RW in presence of periodic coefficients? How the size and the compression points of the breathers are affected by the modulation? In the attempt to answer these important questions, we present the analytical solution of the AB in the presence of periodic modulation of the parameters and analyse how the RW profiles get modified by the variations of the distributed coefficients.
Contribution by the authors
We consider the NLSE in the form
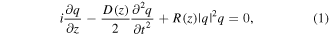
where z and t are the dimensionless propagation distance and time, respectively. The function D(z) then represents the group velocity dispersion coefficient, and R(z) is the nonlinear coefficient. In the following, we will study the NLSE under the integrability condition 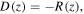 and we will assume the dispersion coefficient to be periodic in the form
and we will assume the dispersion coefficient to be periodic in the form  where
where 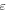 is the amplitude of modulation and
is the amplitude of modulation and  its spatial frequency. To construct the AB with periodic coefficients, we start with a seed solution in the form of plane wave and we use the Darboux transformation method. For
its spatial frequency. To construct the AB with periodic coefficients, we start with a seed solution in the form of plane wave and we use the Darboux transformation method. For  this yields
this yields
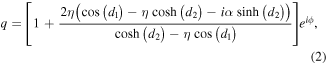
where
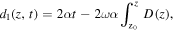
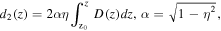
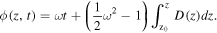
The parameter 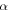 is the growth rate of modulation instability. It is obvious from the analytical solution that the essential characteristics of RW like excitations, namely their magnitude and their periodicity in time, will depend on the values of
is the growth rate of modulation instability. It is obvious from the analytical solution that the essential characteristics of RW like excitations, namely their magnitude and their periodicity in time, will depend on the values of 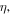
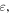 and
and 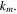 Considering two representative values of
Considering two representative values of 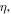 we have depicted the spatio-temporal evolution of the AB with periodic coefficients in figure 27. As can be seen in the figure, the solution (2) exhibits the typical time-periodicity of a breather with period
we have depicted the spatio-temporal evolution of the AB with periodic coefficients in figure 27. As can be seen in the figure, the solution (2) exhibits the typical time-periodicity of a breather with period 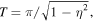 but it is aperiodic in space. The time periodicity and the amplitude of those solutions gradually increase as
but it is aperiodic in space. The time periodicity and the amplitude of those solutions gradually increase as 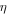 approaches 1. In that limit, the AB converges to the Peregrine soliton. It is also clear that due to the presence of the periodic modulation
approaches 1. In that limit, the AB converges to the Peregrine soliton. It is also clear that due to the presence of the periodic modulation  the spatial profile in z exhibits multiple peaks, a feature that distinguishes it from the standard AB with constant coefficients. Our results reveal that, in general, when
the spatial profile in z exhibits multiple peaks, a feature that distinguishes it from the standard AB with constant coefficients. Our results reveal that, in general, when 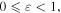 the solution has the same characteristics as in the case of constant coefficients, i.e., the AB is localized in only one point of space and is periodic in time. On the other hand, when
the solution has the same characteristics as in the case of constant coefficients, i.e., the AB is localized in only one point of space and is periodic in time. On the other hand, when 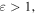 the AB presents now many compression points in space, and the number of these compression points increases as
the AB presents now many compression points in space, and the number of these compression points increases as  increases. The existence of several compression points in space is due to the fact that because of the modulation, there is an energy exchange between the AB and the finite background that changes with the spatial behaviour of the dispersion. At each zero of dispersion, the energy that was smoothly decreasing (increasing) reaches its minimum (maximum), and then increases (decreases) again until it reaches its maximum (minimum) value. The spacing between the multiple compression points is directly determined by the spatial frequency
increases. The existence of several compression points in space is due to the fact that because of the modulation, there is an energy exchange between the AB and the finite background that changes with the spatial behaviour of the dispersion. At each zero of dispersion, the energy that was smoothly decreasing (increasing) reaches its minimum (maximum), and then increases (decreases) again until it reaches its maximum (minimum) value. The spacing between the multiple compression points is directly determined by the spatial frequency 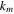 of the modulation. These are the most striking new features of RW with periodic coefficients. Thus, one can control the number and the position of the excited RW by suitably choosing the amplitude of the modulation
of the modulation. These are the most striking new features of RW with periodic coefficients. Thus, one can control the number and the position of the excited RW by suitably choosing the amplitude of the modulation 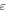 and its spatial frequency
and its spatial frequency 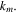 However, an increased value of
However, an increased value of  does not affect the amplitude of the solution. Finally, we also perform direct numerical simulation of equation (1) by the split-step Fourier method with initial condition given by the exact solution (2) at
does not affect the amplitude of the solution. Finally, we also perform direct numerical simulation of equation (1) by the split-step Fourier method with initial condition given by the exact solution (2) at 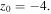 It is well known that the dynamics of the AB without modulation exhibits only one ideal growth-return cycle in propagation distance [162]. However, in the presence of the periodic coefficients, we do not observe in figure 28(a) a single cycle of evolution of the breather, but rather a series of compression-decompression points in space, which are periodic in time. We clearly note in figure 28(b) that increasing the amplitude of periodic modulation
It is well known that the dynamics of the AB without modulation exhibits only one ideal growth-return cycle in propagation distance [162]. However, in the presence of the periodic coefficients, we do not observe in figure 28(a) a single cycle of evolution of the breather, but rather a series of compression-decompression points in space, which are periodic in time. We clearly note in figure 28(b) that increasing the amplitude of periodic modulation 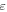 allows us to generate the maximally compressed AB over a shorter propagation distance. One can also see that the increase of
allows us to generate the maximally compressed AB over a shorter propagation distance. One can also see that the increase of 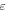 did not influence the maximal amplitude of the AB. Considering the experiments on RW in nonlinear fibers which show the existence of a strongly localized spatio-temporal peak [97], we expect that these multiple compression points could be observed in nonlinear fibers with periodic coefficients.
did not influence the maximal amplitude of the AB. Considering the experiments on RW in nonlinear fibers which show the existence of a strongly localized spatio-temporal peak [97], we expect that these multiple compression points could be observed in nonlinear fibers with periodic coefficients.
Figure 27. Spatio-temporal evolution of Akhmediev breather with periodic coefficients. 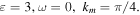
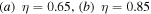 .
.
Download figure:
Standard image High-resolution imageFigure 28. Numerical profile of the Akhmediev breather with periodic coefficients. 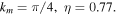

Download figure:
Standard image High-resolution imageConcluding remarks
In summary, we present an exact Akhmediev breather solution of the nonlinear Schrödinger equation with periodic coefficients. Our study reveals that it is possible to generate multiple compression points of the Akhmediev breather solution in many points of the space, by using periodic coefficients. The number of the compression points increases with the amplitude of modulation, while the maximum amplitude of the breather remains unaffected.
Moreover, the numerical simulations of the nonlinear Schrödinger equation with periodic coefficients are performed by the split-step Fourier method, which agree with the analytical results. These results could be of great interest in realizing rogue wave with multiple compression points. Similar studies can be extended to multi-components system. Also the position of the maximum compression points as function of the modulation parameters can be controlled, and work is under progress and will be reported elsewhere.
Acknowledgments and funding information
We acknowledge support from the Laboratoire d'Excellence CEMPI (Centre Européen pour les Mathématiques, la Physique et leurs Interactions).