13 minute read.Matchmaker, matchmaker, make me a match
Matching (or resolving) bibliographic references to target records in the collection is a crucial algorithm in the Crossref ecosystem. Automatic reference matching lets us discover citation relations in large document collections, calculate citation counts, H-indexes, impact factors, etc. At Crossref, we currently use a matching approach based on reference string parsing. Some time ago we realized there is a much simpler approach. And now it is finally battle time: which of the two approaches is better?
TL;DR
- I evaluated and compared four approaches to reference matching: the legacy approach based on reference parsing, and three variants of the new idea called search-based matching.
- A large automatically generated dataset was used for the experiments. It is composed of 7,374 metadata records from the Crossref collection, each of which was formatted automatically into reference strings using 11 citation styles.
- The main metrics used for the evaluation are precision and recall. I also use F1 as a standard metric that combines precision and recall into a single number, weighing them equally. All values are calculated for each metadata record separately and averaged over the dataset.
- In general, search-based matching is better than the legacy approach in F1 and recall, but worse in precision.
- The best variant of search-based matching outperforms the legacy approach in average F1 (84.5% vs. 52.9%), with the average precision worse by only 0.1% (99.2% vs 99.3%), and the average recall better by 88% (79.0% vs. 42.0%).
- The best variant of search-based matching also outperforms the legacy approach in average F1 for each one of the 11 styles.
- A weak spot of the parsing-based approach is degraded/noisy reference strings, which do not appear to use any of the known citation styles.
- A weak spot of search-based approach is short reference strings, and in particular citation styles that do not include the title in the reference string.
Introduction
In reference matching, on the input we have a bibliographic reference. It can have the form of an unstructured string, such as:
(1) Adamo, S. H.; Cain, M. S.; Mitroff, S. R. Psychological Science 2013, 24, 2569–2574.
The input can also have the form of a structured reference, such as (BibTex format):
@article{adamo2013,
author = {Stephen H. Adamo and Matthew S. Cain and Stephen R. Mitroff},
title = {Self-Induced Attentional Blink: A Cause of Errors in Multiple-Target Search},
journal = {Psychological Science},
volume = {24},
number = {12},
pages = {2569-2574},
year = {2013}
}
The goal of matching is to find the document, which the input reference points to.
Matching algorithms
Matching references is not a trivial task even for a human, not to mention the machines, which are still a bit less intelligent than us (or so they want us to believe…). A typical meta-approach to reference matching might be to score the similarity between the input reference and the candidate target documents. The document most similar to the input is then returned as the target.
Of course, still a lot can go wrong here. We can have more than one potential target record with the same score (which one do we choose?). We can have only documents with low to medium scores (is the actual target even present in our collection?). We can also have errors in the input string (are the similarity scores robust enough?). Life’s tough!
The main difference between various matching algorithms is in fact how the similarity is calculated. For example, one idea might be to compare the records field by field (how similar is the title/author/journal in the input reference to the title/author/journal of our candidate target record?). This is roughly how the matching works currently at Crossref.
The main problem with this approach is that it requires a structured reference, and in practise, often all we have is a plain reference string. In such a case we need to extract the metadata fields from the reference string (this is called parsing). Parsing introduces errors, since no parser is omniscient. The errors propagate further and affect the scoring… you get the picture.
Luckily, as we have known for some time now, this is not the only approach. Instead of comparing structured objects, we could calculate the similarity between them using their unstructured textual form. This effectively eliminates the need for parsing, since the unstructured form is either already available on the input or can be easily generated from the structured form.
What about the similarity scores? We already know a powerful method for scoring the similarities between texts. Those are (you guessed it!) scoring algorithms used by search engines. Most of them, including Crossref’s, do not need a structured representation of the object, they are perfectly happy with just a plain text query.
So all we need to do is to pass the original reference string (or some concatenation of the reference fields, if only a structured reference is available) to the search engine and let it score the similarity for us. It will also conveniently sort the results so that it is easy to find the top hit.
Evaluation
So far so good. But which strategy is better? Is it better to develop an accurate parser, or just rely on the search engine? I don’t feel like guessing. Let’s try to answer this using (data) science. But first, we need to decompose our question into smaller pieces.
Question 1. How can I measure the quality of a reference matcher?
Generally speaking, this can be done by checking the resulting citation links. Simply put, the better the links, the better the matching approach must have been.
A few standard metrics can be applied here, including accuracy, precision, recall and F1. We decided to calculate precision, recall and F1 separately for each document in the dataset, and then average those numbers over the entire dataset.
When I say “documents”, I really mean “target documents”:
- precision for a document X tells us, what percentage of links to X in the system are correct
- recall for a document X tells us, what percentage of true links to X are present in the system
- F1 is the harmonic mean of precision and recall
F1 is a single-number metric combining precision and recall. In F1 precision and recall are weighted equally. It is also possible to combine precision and recall using different weights, to place more emphasis on one of those metrics.
We decided to look at links from the target document’s perspective, because this is what the academic world cares about (i.e. how accurate the citation counts of academic papers are).
Calculating separate numbers for individual documents and averaging them within a dataset is the best way to have reliable confidence intervals (which makes the whole analysis look much smarter!).
Question 2. Which approaches should be compared?
In total we tested four reference matching approaches.
The first approach, called the legacy approach, is the approach currently used in Crossref ecosystem. It uses a parser and matches the extracted metadata fields against the records in the collection.
The second approach is the search-based matching (SBM) with a simple threshold. It queries the search engine using the reference string and returns the top hit from the results, if its relevance score exceeds the threshold.
The third approach is the search-based matching (SBM) with a normalized threshold. Similarly as in the simplest SBM, in this approach we query the search engine using the reference string. In this case the first hit is returned if its normalized score (the score divided by the reference length) exceeds the threshold.
Finally, the fourth approach is a variation of the search based matching, called search-based matching with validation (SBMV). In this algorithm we use additional validation procedure on top of SBM. First, SBM with a normalized threshold is applied and the search results with the scores exceeding the normalized threshold are selected as candidate target documents. Second, we calculate validation similarity between the input string and each of the candidates. This validation similarity is based on the presence of the candidate record’s metadata fields (year, volume, issue, pages, the last name of the first author, etc.) in the input reference string, as well as the relevance score returned by the search engine. Finally, the most similar candidate is returned as the final target document, if its validation similarity exceeds the validation threshold.
By adding the validation stage to the search-based matching we make sure that the same bibliographic numbers (year, volume, etc.) are present in both the input reference and the returned document. We also don’t simply take the first result, but rather use this validation similarity to choose from results scored similarly by the search engine.
All the thresholds are parameters which have to be set prior to the matching. The thresholds used in these experiments were chosen using a separate dataset, as the values maximizing the F1 of each algorithm.
Question 3. How to create the dataset?
Results
We could try to calculate our metrics for every single document in the system. Since we currently have over 100M of them, this would take a while, and we already felt impatient…
A faster strategy was to use sampling with all the tools statistics was so generous to provide. And this is exactly what we did. We used a random sample of 2500 items from our system, which is big enough to give reliable results and, as we will see later, produces quite narrow confidence intervals.
Apart from the sample, we needed some input reference strings. We generated those automatically by formatting the metadata of the chosen items using various citation styles. (Similarly to what happens when you automatically format the bibliography section for your article. Or at least we hope you don’t produce those reference strings manually…)
For each record in our sample, we generated 11 citation strings, using the following styles:
- Well known citation styles from various disciplines:
- american-chemical-society (acs)
- american-institute-of-physics (aip)
- elsevier-without-titles (ewt)
- apa
- chicago-author-date
- modern-language-association (mla)
- Known styles + random noise. To simulate not-so-clean data, we randomly added noise (additional spaces, deleted spaces, typos) to the generated strings of the following styles:
- american-institute-of-physics
- apa
- Custom degraded “styles”:
- degraded: a simple concatenation of authors’ names, title, container title, year, volume, issue and pages
- one author: a simple concatenation of the first author’s name, title, container title, year, volume, issue and pages
- title scrambled: same as degraded, but with title words randomly shuffled
Some styles include the DOI in the reference string. In such cases we stripped the DOI from the string, to make the matching problem non-trivial.
An ideal matching algorithm will match every generated string to the record it was generated from. In practise, some of the expected matches will be missing, which will lower the recall of the tested matching approach. On the other hand, it is very probable that we will get the precision of 100%. To have the precision lower than 100%, we would have to have some unexpected matches to our sampled documents, which is unlikely. This is obviously not great, because we are missing a very important piece of information.
What can we do to “encourage” such mismatches to our sampled documents? We could generate additional reference strings of documents that are not in our sample, but are similar to the documents in our sample. Hopefully, we will see some incorrect links from those similar strings to our sampled documents.
For each sampled document I added up to 2 similar documents (I used, surprise surprise, our search engine to find the most similar documents). I ended up with 7,374 items in total (2,500 originally sampled and 4,874 similar items). For each item, 11 different reference strings were generated. Each reference string was then matched using the tested approaches and I could finally look at some results.
Results
First, let’s compare the overall results averaged over the entire dataset:
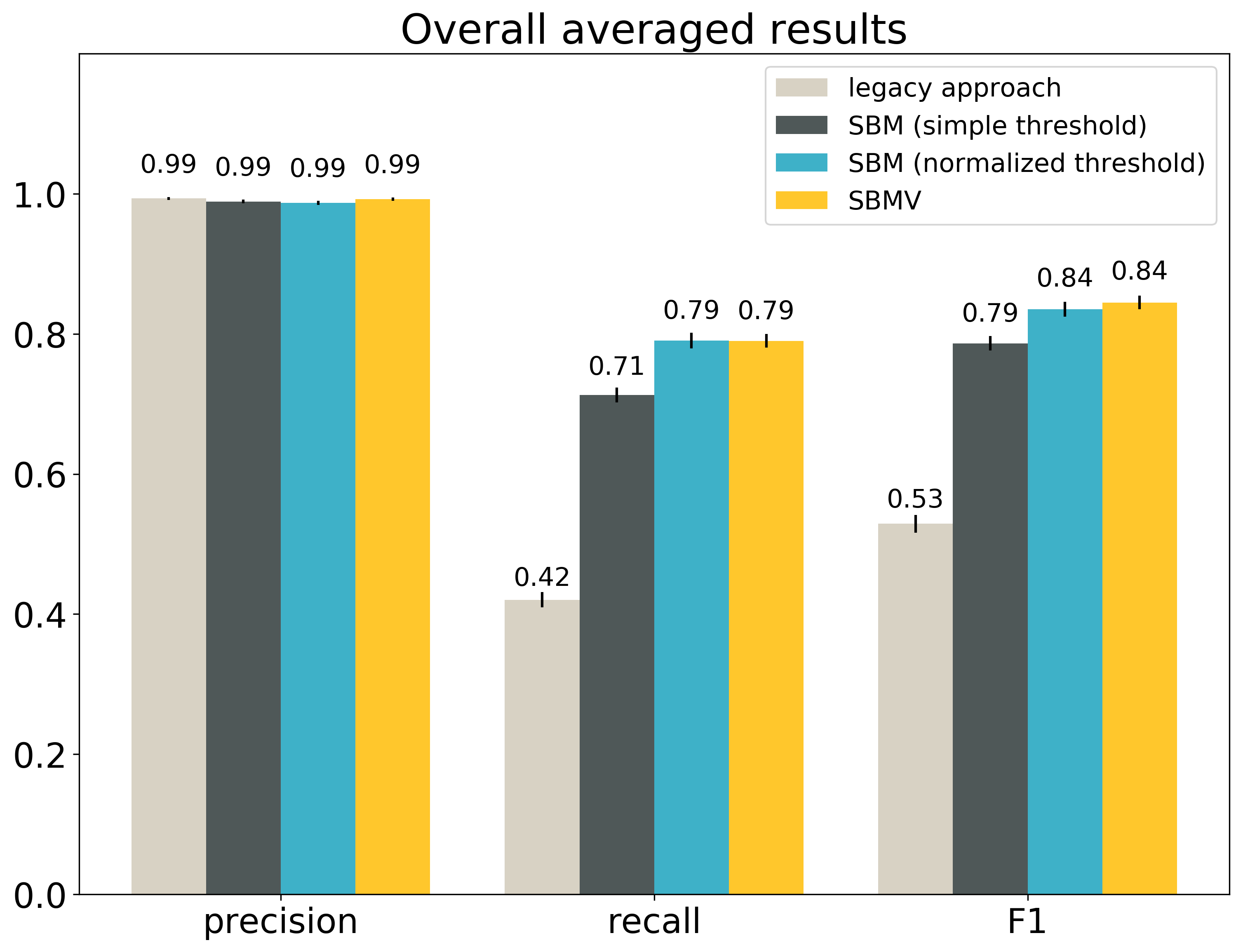
The small vertical black lines at the top of the boxes show the confidence intervals at the confidence level 95%. The table gives the exact values and the same confidence intervals. The best result for each metric is bolded.
| average precision | average recall | average F1 |
|---|
| legacy approach | 0.9933
(0.9910 - 0.9956) | 0.4203
(0.4095 - 0.4312) | 0.5289
(0.5164 - 0.5413) |
| SBM (simple threshold) | 0.9890
(0.9863 - 0.9917) | 0.7127
(0.7021 - 0.7233) | 0.7866
(0.7763 - 0.7968) |
| SBM (normalized threshold) | 0.9872
(0.9844 - 0.9901) | 0.7905
(0.7796 - 0.8015) | 0.8354
(0.8249 - 0.8458) |
| SBMV | 0.9923
(0.9902 - 0.9945) | 0.7902
(0.7802 - 0.8002) | 0.8448
(0.8352 - 0.8544) |
The confidence intervals given in the table are the ranges, in which it is 95% likely to have the real average precision, recall and F1. For example, we are 95% sure that the real F1 for SBMV in our entire collection is within the range 0.8352 - 0.8544.
As we can see, each metric has a different winner.
The legacy approach is the best in precision. This suggests the legacy approach is quite conservative and outputs a match only if it is very sure about it. This might also result in missing a number of true matches (false negatives).
According to the paired Student’s t-test, the difference between the average precision of the legacy approach and the average precision of the second best SBMV is not statistically significant. This means we cannot rule out that this difference is simply the effect of the randomness in sampling, and not the sign of the true difference.
SBM with a normalized threshold is the best in recall. This suggests that it is fairly tolerant and returns a lot of matches, which might also result in returning more incorrect matches (false positives). Also in this case the difference between the winner and the second best (SBMV) is not statistically significant.
SBMV is the best in F1. This shows that this approach balances precision and recall the best, despite being only the second best in both of those metrics. According to the paired Student’s t-test, the difference between SBMV and the second best approach (SBM with a normalized threshold) is statistically significant.
All variants of the search-based matching outperform the parsing-based approach in terms of F1, with statistically significant differences. This shows that in search based-matching it is possible to keep precision almost as good as in the legacy approach, and still include many more true positives.
Let’s also look at the same results split by the citation style:
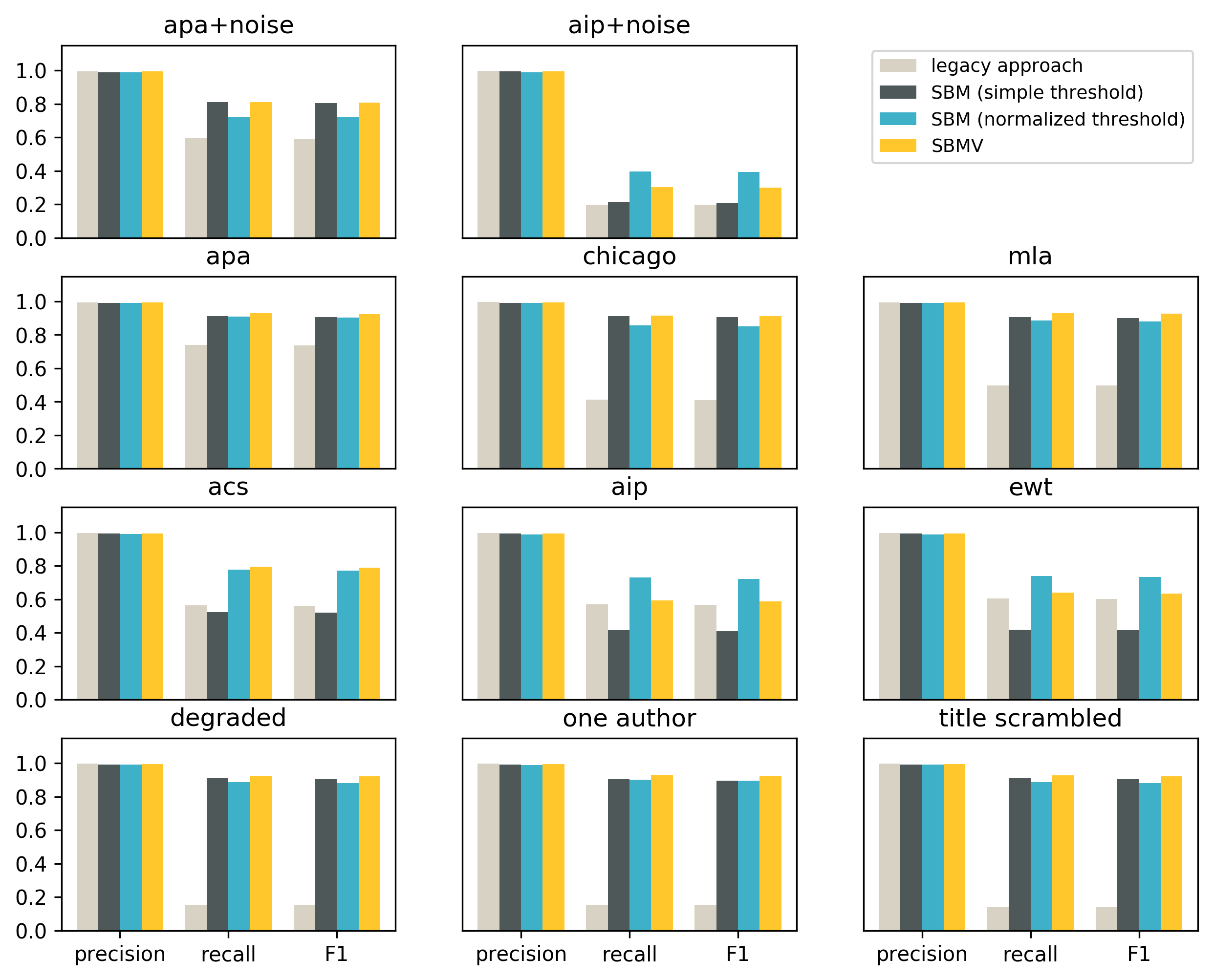
For all styles the precision values are very high, and the legacy approach is slightly better than all variations of the search-based approach.
In terms of recall and F1 SBM with a simple threshold is better than the legacy approach in 8 out of 11 styles. The three styles for which the legacy approach outperforms SBM with a simple threshold are styles that do not include the title in the reference strings (acs, aip and ewt). The reason for this is that the simple threshold cannot be well calibrated for shorter and longer reference strings at the same time.
SBM with a normalized threshold and SBMV is better than the legacy approach in recall and F1 for all 11 styles.
The weak spot of the legacy approach is degraded and noisy reference strings, which do not appear to use any of the known citation styles.
The weak spot of the search-based matching is short reference strings, and in particular citation styles that do not include the title in the string.
Limitations
The limitations are related mostly to the method of building the dataset.
- All the numbers reported here are estimates, since they were calculated on a sample.
- The numbers show strengths and weaknesses of each approach, but they do not reflect the real precision and recall in the system:
- Since we included only 2 similar documents for each document in the sample, precision is most likely lower in the real data.
- We used a number of styles distributed uniformly. Of course in the real system the styles and their distribution might be different, which affects all the calculated numbers.







